Coupe de Pythagore/ Atanas Amosse/ Julia Nicolai/ Ismael Culit-Ba

Coordonnées

• Noms : Atanas Amosse ; Julia Nicolai ; Ismael Culit-Ba

• Adresse e-mail : atanas.amosse@sorbonne-universite.fr, julia.nicolai@sorbonne-universite.fr, ismael.culitba@sorbonne-universite.fr

Introduction

• Date de début : 12/03/2025
  

• Date de fin : 9/04/2025

• Objectifs : On cherche ici à conceptualiser une simple coupe, possédant en son milieu un tube qu'on appellera par la suite tube central et qui permet de créer un phénomène de siphon vidant tout le volume du fluide introduit dans la coupe lorsqu'il aura atteint une certaine hauteur. Cette conceptualisation se fera à travers deux coupes qui reposent sur le même principe physique, mais qui ont une modélisation différente.

• Contexte : Ce projet s'inscrit dans le cadre de l'UE ARE Magie, ou nous avons comme projet de donner une impression de magie à des personnes novices de préférence aux différents concepts scientifiques, car en soit notre tour ne repose que sur une explication claire corrélant principes mathématiques et physiques. 

Matériaux / Machines :

• Modélisation : Blender

• Matériaux : PLA Blanc 1,75 mm (15g)

• Impression 3D : Prusa MK4S (PLA)

• Slicer : PrusaSlicer

• Fluide : Eau

Conceptualisation / Modélisation / Réalisation :

Dans un premier temps nous avons mis au point un premier modèle de coupe à partir duquel nous nous sommes appuyés pour créer nos éléments suivants, et en particulier nos deux coupes différentes. Ce modèle de coupe s'obtient en alliant des cylindres et des demi-sphères. De façon brève cette coupe possède un tube central avec deux trous circulaires à sa base permettant l'entrée du fluide lors de son versement dans la coupe ainsi qu'un trou circulaire sous la coupe permettant la sortie du fluide par le bas. Ce fluide grâce à un conduit va alors remonter jusqu'à une certaine hauteur (partie sommitale du tube) et par le biais d'un nouveau conduit se déverser vers le bas jusqu'à rejoindre notre trou circulaire, permettant donc au fluide de sortir. Pour la suite de nos explications et par souci de clarté nous appellerons le tube central le tube 1 et le tube à l'intérieur de ce dernier le tube 2.

Mais ici il ne faut pas oublier de se poser la question suivante : comment savions-nous quel type de diamètre il fallait à la fois pour le tube 1 ainsi que pour le tube 2 pour permettre un écoulement du fluide le plus optimal ? Nous avons donc résolu ce problème en deux temps. Tout d'abord pour le tube 2 nous avons modélisé 3 tubes de diamètre différent et effectué un siphonage sur chacun d'eux. Il faut savoir ici que les 3 diamètres n'ont pas été choisi arbitrairement mais résulte d'une estimation.

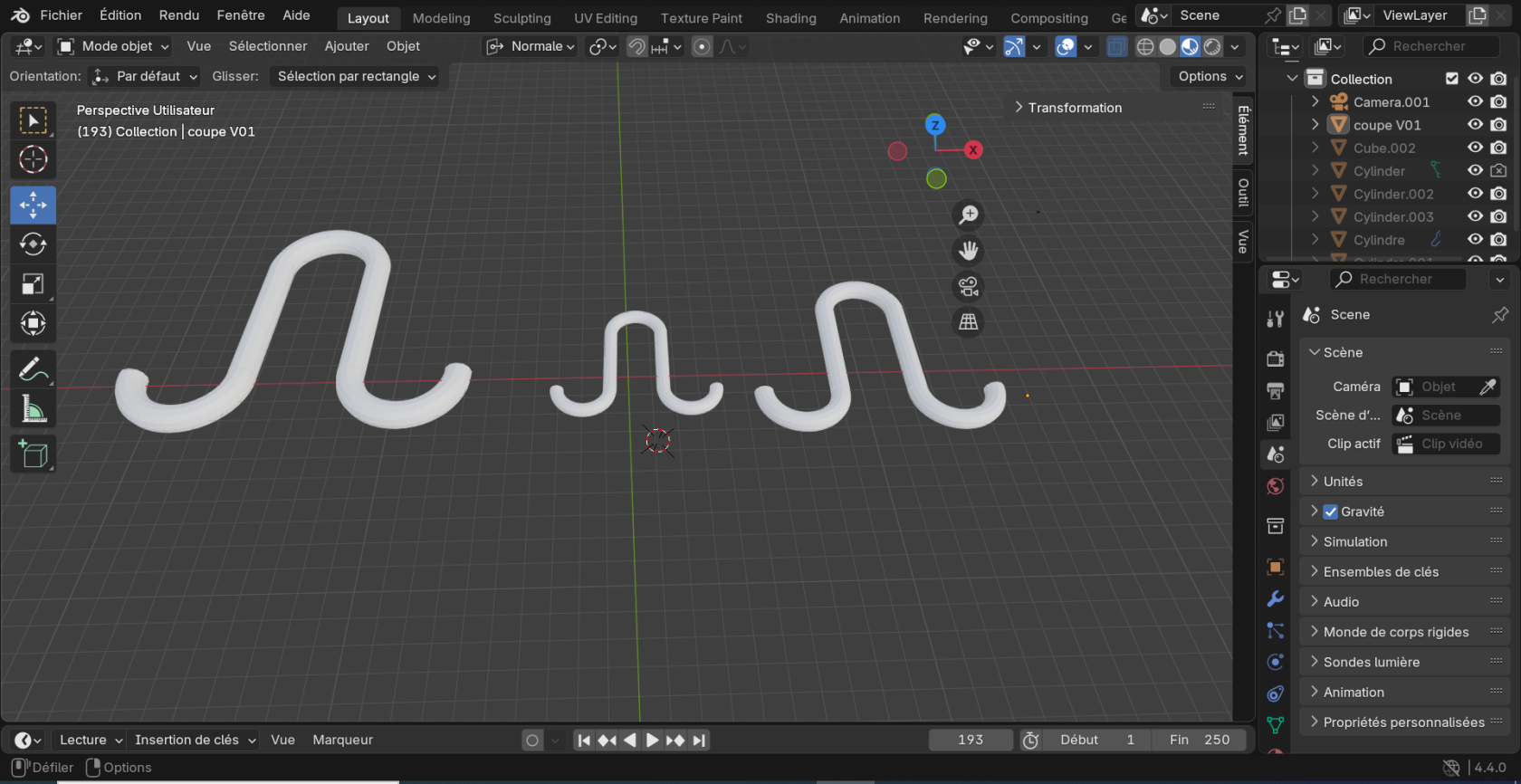
Modèle des 3 tubes de diamètres différents :

NB : les 3 tubes sont recourbés de chaque côté car cela permet de ne pas les tenir avec les mains mais de simplement les mettre dans un récipient rempli pour effectuer le siphonage. En effet le fait que les 3 tubes soit recourbés de chaque côté permet d'apporter une stabilité du fluide à l'intérieur et de l'empêcher de s'écouler tant qu'il n'est pas dans un récipient quelconque.

La réalisation précédente nous a donc permis de nous fixer sur le diamètre qu'il fallait donc donner au tube 2 car c'est dans ce dernier que l'eau s'écoulera vers le bas (cf : modèle 2). Pour ce qui est du tube 1, nous l'avons également estimé par rapport à la place qu'il prendrait dans un verre lambda et en nous appuyons de différents schémas sur internet. Mais de façon générale il devait être légèrement supérieur au tube 2 ce qui nous offrait déjà une bonne estimation.

Modèle 1 de la coupe en entier (en haut) et modèle 2 de la coupe coupé en deux avec légende (en bas) :

Une fois ce premier modèle effectué, on constate que ce dernier possède sur la partie sommital du tube central un toit droit. On est donc amené à se demander quel type de forme pour la partie sommital permet le meilleur écoulement de l'eau au travers le tube. Pour répondre à cette question nous avons donc dans un premier temps supprimer la partie sommitale du tube, et nous avons modéliser en parallèle deux "capuchons", le premier étant une demi-sphère et le second un cylindre. Il s'agit ici de deux capuchons que l'on placera par la suite sur la partie sommitale de notre tube central et que l'on maintiendra avec notre doigt afin de voir dans quel cas l'écoulement de l'eau est le plus optimal.

Modèle de la coupe sans sa partie sommitale ainsi que nos deux capuchons :

Nous avons donc fini ici notre premier modèle de coupe. Pour réaliser notre seconde coupe nous allons récupérer le modèle que nous venons de mettre au point c'est-à-dire celui de la coupe sans la partie sommitale. On cherche ici, à y placer une "paille" que l'on imbrique à l'intérieur du tube 2, et non pas dans l'espace entre les tubes 1 et 2, pour garantir la meilleur étanchéité possible. Ainsi lorsque le fluide sera verser dans la coupe il rentrera par la "paille" jusqu'à atteindre le "point de basculement" qui correspond donc ici au moment ou l'eau passera dans l'autre partie de la paille. Pour cela il nous faut faire correspondre les diamètres entre la paille et le tube central pour que la "paille" s'y imbrique le mieux et que l'étanchéité soit maximale. Seulement avant de faire correspondre les diamètres entre la coupe et la "paille", il nous faut savoir quel est le diamètre de la "paille" favorisant un écoulement de l'eau le plus optimal. Pour ce faire, il nous suffit juste ici de nous inspirer des 3 tubes fabriqués au début. En effet pour rappel nous cherchions au tout début à savoir quelle diamètre fallait-il prendre pour le tube 1 et notamment pour le tube 2. Etant donné que l'on va imbriqué notre "paille" dans le tube 2 il nous suffit juste de reprendre le diamètre du tube 2 et de l'appliqué à notre paille, moyennant une petite réduction du diamètre car la paille sera bien à l'intérieur et non pas sur le tube 2.

Une fois fixé sur quel diamètre de la "paille" l'écoulement de l'eau serait le meilleur à partir tout simplement du diamètre attribué au tube 2, nous avons donc conçu notre premier modèle de "paille". 

Premier modèle de "paille" :

Seulement après réflexion, nous avons conclut que ce modèle de paille n'était pas optimal. En effet, le principe ici est de vraiment créer une paille en forme de U, afin de permettre au maximum la vidange du verre. On constate ici que ce n'est pas le cas avec notre modèle de paille car cette dernière possède un côté trop court. Ainsi lorsque l'eau commencera à sortir de la coupe, cette dernière s'arrêtera à la hauteur du bas de la paille. Ce côté n'étant donc pas assez long, une grande partie du fluide restera dans la coupe et ne sortira pas. Pour résoudre ce problème, on a donc allonger le côté de la paille de façon à obtenir un U parfait.

Modèle final de la "paille" : 

Une fois notre modèle de "paille" correctement conçu, nous touchions pratiquement au but. Il nous fallait désormais résoudre les problèmes d'étanchéité. En effet, en insérant simplement la "paille" dans notre coupe directement, deux problèmes se posent à nous. Le premier comment trouver le moyen de venir fermer la partie sommitale du tube central, et le second comment empêcher l'eau de rentrer par les deux trous circulaires à la base du tube central.

Pour résoudre notre premier problème, nous avons donc modéliser un cylindre avec le même diamètre que notre tube central et possédant exactement en son centre un trou correspondant au diamètre de notre "paille". De cette façon il suffira juste de positionner notre "paille", dans le trou du cylindre permettant ainsi de rendre étanche notre partie sommitale du tube central puisque ce dernier sera donc boucher.

Enfin pour résoudre notre second problème, nous avons à nouveau modéliser un cylindre avec trou dedans correspondant au diamètre du tube central. De cette façon il suffira seulement de le faire glisser le long du tube central jusqu'à sa base de façon à ce qu'il puisse venir combler les deux trous circulaires. Bien évidement le cylindre possède une hauteur supérieur à celle des trous afin d'être sur que ces derniers seront bien bouchés.

Modèle de la coupe avec tous ses éléments complémentaires (en haut) et modèle de la coupe en version finale avec tous ses éléments imbriqués dessus (en bas) :

Recherche documentaire :

https://ressources.univ-lemans.fr/AccesLibre/UM/Pedago/physique/02/divers/coupepyta.html

https://fr.wikipedia.org/wiki/Coupe_de_Pythagore

https://objetsscientifiques.com/verre-de-pythagore

https://www.youtube.com/watch?v=A-YMHXuiaWw

Annexe :

Fichier blender donnant accès aux différentes modélisations : 

Modèle des 3 tubes de diamètres différents.blend

Modèle de la coupe en entier.blend

Modèle de la coupe sans partie sommitale avec les capuchons.blend

Modèle paille finale.blend

Modèle de la coupe avec tous les éléments complémentaires.blend