Computational Fluid Dynamics (CFD) applied to Formula 1 study
                     "Dynamique des fluides numérique appliquée à l'étude d'une Formule 1"

• *Membres de l'équipe: * Anthony GUILLARD (anthony.guillard@etu.upmc.fr) * Enzo RONGIONE (enzo.rongione@etu.upmc.fr) * Hector PAPAGEORGIOU-VERNICOS (hector.papageorgiou-vernicos@etu.upmc.fr) * Christophe WILK (christophe.wilk@etu.upmc.fr) Encadrante: Giovanna LANI (giovanna.lani@impmc.upmc.fr) Responsable de l'UE: Vincent DUPUIS (vincent.dupuis@upmc.fr) Dates du projet: * Début du projet: 26/01/17 * Premier rendez-vous pédagogique: 16/02/17 * Second rendez-vous pédagogique: 24/03/17 * Clôture du wiki: 31/03/17 * Troisième rendez-vous pédagogique: prévu au retour des vacances de Pâques * Dépôt de l'article: 24/04/17 * Journée de présentation: 26/04/17 ===== Présentation du projet ===== ==== Problématique ==== Quelles sont les contraintes aérodynamiques qui ont poussé les écuries à modéliser les Formules 1 telles qu'on les connait ? ==== Objectifs ==== Le but de ce travail est de comprendre en quoi la forme caractéristique d'une Formule 1 permet le rôle majeur que l'on lui connaît, c'est-à dire un idéal de vitesse et de performances afin d'assurer la victoire au pilote et à l'écurie. Ce projet nous permet, outre le fait de produire une étude sur le profil d'une Formule 1, d'acquérir un certain nombre de compétences théoriques et expérimentales: * Analyser la théorie derrière le profil d'une Formule 1 * Maîtriser les principes de l'hydrodynamique * Utiliser une imprimante 3D * Utiliser une soufflerie * Programmer les trajectoires afin de les mettre en graphe * Coder des lignes de courant passant sur la Formule 1 * Rédiger en LaTeX de manière rigoureuse ===== Organisation du projet ===== ==== Répartition des tâches et rôles ==== Au sein de cette section, vous pourrez accéder à des diagrammes de Gantt définissant une vue globale des tâches du projet et de leurs répartitions auprès des membres du groupe: le premier réalisé en début du projet et le deuxième, une fois le projet terminé. —- Rôles: Anthony (animateur), Enzo (intendant), Hector (secrétaire), Christophe (scribe), Giovanna LANI (tuteur) Diagramme de Gantt initial: Diagramme de Gantt rétrospectif: ==== Ressources et budget ==== Ici nous établissons une liste du matériel et des outils utilisés, ainsi qu'un budget prévisionnel. —- Ressources utilisées: * Logiciels d'ogranisation et de rédaction: GanttProject (gratuit), ShareLaTeX (en ligne, gratuit) * Langage de programmation: environnement Python (gratuit) * Logiciel de calcul formel: Mathematica (licence gratuit accordée par l'UPMC à tous les étudiants) * Logiciel d'acquisition et de pointage vidéo: Cineris (gratuit) * Logiciel de bureautique: LibreOffice (gratuit) * Logiciels en lien avec l'imprimante 3D: visionneuse STL (gratuit), UP! (impression 3D, gratuit) * Logiciels spécialisés pour des souffleries numériques: Xfoil (gratuit, écrit par l’équipe de DRELA M. du MIT, peu pratique mais très sophistiqué - http://web.mit.edu/drela/Public/web/xfoil/), Javafoil (gratuit, écrit par HEPPERLE M., plus simple mais moins complet - http://www.mh-aerotools.de/airfoils/javafoil.htm) * Machines: Imprimante 3D, soufflerie, caméra * Bibliothèque de maquettes: Thingiverse * Bibliothèque de données (UIUC): http://m-selig.ae.illinois.edu/ads/coord_database.html * Supports académiques: Bibliographie * Supports multimédias: wiki:projet:aerodyn_f1 Budget prévisionnel: * Utilisation du PMClab: l'adhésion est prise en charge dans le cadre de l'enseignement (gratuit) * Solutions informatiques: les logiciels utilisés sont gratuits * Fabrication des maquettes: on compte environ 50 g pour une maquette imprimée en ABS ou PLA (filaments plastiques, prix: 0,05 €/g) soit environ 2.5€ la maquette → pour quatre maquettes, on pense d'allouer 10€ de budget → montant alloué au final: pas plus de 10€ pour les quatre maquettes, avec un total de 170 g * Soufflerie: utilisation gratuite à l'Atrium à la plateforme de Physique ==== Journal de bord ==== Dans cette section, vous trouverez un résumé détaillé de chaque tâche effectuée en rapport avec le projet, ainsi que le volume horaire consacré. —- === 18/01/17 === (Anthony, Enzo, Hector - 1H00) Détermination du sujet autour de la Formule 1, hésitation initial entre l'effet Leidenfrost et l'étude des ailes d'avions Problème rencontré: trouver le bon compromis entre un sujet réalisable, intéressant et assez profond —- === 25/01/17 === Sujet et groupe validés par l'équipe pédagogique, début du projet —- === 26/01/17 === (Enzo, Anthony - 1H00) Réunion : création du wiki, définir les objectifs du projet et une problématique —- === 28/01/17 === (Anthony, Enzo - 1H00) Brainstorming sur les tâches à réaliser, contact avec l'encadrante —- === 01/02/17 === (Christophe, Hector, Enzo, Anthony - 1H00) Réunion: diagramme de Gantt préliminaire, utilisation du logiciel GanttProject, familiarisation avec ses outils (Anthony, Enzo - 1H00) détermination du rôle de chacun (scribe, intendant, animateur, etc…) Tâches réalisées: nous avons fini le diagramme de Gantt initial afin de nous fixer des deadlines (mais qui restent flexibles tout de même) et nous savons réaliser un diagramme de Gantt afin de bien manipuler pour le diagramme rétrospectif. —- === 03/02/17 === (Christophe, Hector, Enzo, Anthony - 0H30) Esquisse d'un budget, des ressources nécessaires/à disposition Problème rencontré: Estimation du coût d'une maquette vu que le prix varie en fonction du poids, on a également dû prendre en compte la possibilité de devoir construire notre propre soufflerie dans le budget afin de ne pas le dépasser, nous nous sommes alors renseignés sur les méthodes de fabrication d'une soufflerie —- === 06/02/17 === Premier retour de l'encadrante sur nos avancées: diagramme de Gantt satisfaisant, lancement dans les tâches de recherches documentaires —- === 07/02/17 === (Enzo - 1H00) Prise de contact avec le PMClab, interrogations sur les coûts d'impression et la faisabilité des maquettes, découverte des outils à disposition comme la découpeuse laser, les imprimantes 3D, les postes à disposition, etc… —- === 08/02/17 === (Enzo, Anthony, Hector - 1H00) Réunion : nous avons défini les objectifs de la semaine qui sont le(s) contact(s) avec des professionnels et trouver une maquette. Nous avons réalisé la détermination des ressources et finalisation du budget —- === 09/02/17 === (Anthony- 1H00) Recherche sur les écuries de F1, envoi d'emails afin de leur demander des conseils et quelques guidelines Question rhétorique: je me demande si ceci va être concluant vu que les écuries sont surchargées, je doute de leur capacité à me répondre et à m'aider dans mes recherches ? —- === 10/02/17 === (Enzo - 2H00) Recherches documentaires sur la dynamique des fluides: équations fondamentales dans le cas des fluides compressibles non visqueux comme l'air, nombre de Mach « 0.3, équation de l'écoulement, approximations aérodynamismes ; on part de la base de la dynamique des fluides pour construire notre modèle —- === 11/02/17 === (Enzo - 2H00) Recherches documentaires sur les méthodes de simulation numériques dans le cadre d'une étude de dynamique des fluides: application directe de la dynamique des fluides à l'aérodynamisme, contact avec l'encadrante (Anthony - 1H30) Recherches documentaires sur les concepts théoriques de l'aérodynamique, différents types d'écoulement (incompressible vs compressible: je trouve que le nombre de Mach est le facteur déterminant), familiarisation avec les équations régissant l'aérodynamisme, détermination des forces s'appliquant sur une F1, recherches sur les variations du coefficient de traînée selon le profil du corps —- === 15/02/17 === (Enzo, Anthony, Hector, Christophe - 1H00) Réunion : nous avons fait le point sur les recherches effectuées et nous avons défini les objectifs de la semaine → rencontrer l'encadrante, trouver une soufflerie en prenant contact avec la plateforme expérimentale de Physique de l'UPMC, imprimer les maquettes au PMClab, poursuivre les recherches documentaires en se concentrant sur la modélisation numérique et les coefficients aérodynamiques (Christophe - 2H00) Recherches documentaires sur la dynamique des fluides appliqué à l'automobile : aérodynamique automobile, traînée, déportance, grandeurs aérodynamiques —- === 16/02/17 === (Anthony, Christophe - 1H00) Rencontre avec l'encadrante afin de parler des deadlines et des exigences envers le projet. On a de bons retours sur notre projet pour le moment, on va continuer à persévérer dans la théorie et bientôt commencer nos expériences afin de ne pas prendre de retard (Christophe - 0H30) Recherche et prise de contact avec des acteurs extérieurs au projet pour acquérir le matériel nécessaire (Hector - 1H00) Recherche documentaire sur la dynamique des fluides, recherche sur les équations de mouvement d'écoulement de fluide —- === 17/02/17 === (Christophe, Anthony, Enzo - 0H30) Impression de la première F1 en 3D au PMClab Tâche réalisée: comprendre comment marche une imprimante 3D (→ par superposition de filaments de plastique) et comment l'opérer, c'est-à-dire par quel moyen s'en servir. On interagit avec par l'intermédiaire d'un logiciel (UP!) qui importe des fichiers .stl et qui nous fait visualiser le rendu final. (Enzo - 0H15) Renseignements sur la soufflerie à la plateforme expérimentale de Physique, utilisation possible en Atrium 5e étage, libre car aucun TP associé, il suffit d'aller voir le technicien pour lui demander l'accès à la salle —- === 19/02/17 === (Anthony - 1H00) Recherche documentaire sur la force de traînée et de portance, sur leur différentes composantes (pression et de frottement) —- === 20/02/17 === (Anthony, Christophe - 0H30) Impression de la voiture en 3D au PMClab, nous avons consolidé notre compréhension de l'imprimante 3D et on a pu l'utiliser sans l'aide des techniciens du PMClab Remarque relative à l'impression: on remarque plus sur cette maquette que sur la précédente la précision approximative de l'imprimante et la présence ,ici encore plus contraignante, du support d'impression qui entoure même l'impression au niveau des roues( ce qui le rend difficile à enlever sous peine d'abimer la maquette). Bien sur ce ne sont que des détails qui ne devraient pas gêner notre prise de données lors de l'expérience. —- === 21/02/17 === (Anthony, Enzo - 0H30) Impression du cube au PMClab Problème rencontré: l'imprimante n'a pas bien chauffé au début, du coup une des faces du cube est un peu penchée/écrasée → aucun impact sur nos mesures, il nous suffit de montrer dans la soufflerie le cube du bon côté non altéré pour obtenir de bonnes mesures, de plus nous avons que le coefficient de traînée du cube est relativement élevé comparé aux structures aérodynamiques (de l'ordre de 1) —- === 22/02/17 === (Anthony, Enzo, Christophe - 0H30) Impression de la deuxième F1 au PMClab (Enzo, Anthony, Hector, Christophe - 0H45) Réunion: bilan sur l'avancement des recherches documentaires, objectifs de la semaine: commencer les expériences, continuer les recherches, aborder les modélisations —- === 24/02/17 === (Enzo - 1H00) Recherches sur le coefficient de traînée avec table de valeurs, exemple de visualisation des écoulements fluides rencontrant un obstacle → expérience d'Étienne-Jules Marey (1830-1904), machine à fumée. On remarque que les coefficients de traînée sont sans unité et interviennent naturellement dans la force de traînée (selon x). On distingue plusieurs forces aérodynamiques → la traînée selon x, la dérive selon y et la portance selon z (Hector - 0H30) Etude des équations de Navier-Stokes qui permettent de décrire l'écoulement des fluides turbulent autour d'une surface. Dans notre étude avec la vitesse des véhicules étudiés, on a nombre de Reynolds grand, principalement car nous sommes avec des vitesses suffisamment élevées, ce qui va provoquer des flots turbulents. —- === 28/02/17 === (Enzo - 1H30) Préparation des expérimentations du mercredi 01/03: protocole expérimental, calcul appliqué du nombre de Mach, détermination des forces en présence, expression des coefficients aérodynamiques, expression des surfaces de référence dans le cas du cube, des F1 et de la voiture, détermination approchée de la masse volumique de l'ai par la loi des gaz parfaits et comparaison théorique, définition de la finesse —- === 01/03/17 === (Enzo - 2H00) Problème majeur lié à l'expérimentation: je m'étais bien renseigné le 17/02 au bureau du technicien de la plateforme de L1 Physique à l'Atrium, ce dernier m'avait alors dit que l'accès à la salle de TP était libre et qu'il suffisait de déposer noms prénoms sur une feuille au bureau pour obtenir les clés; cependant, nous sommes tous allés ce matin demander l'accès, le technicien n'était plus le même et ce dernier nous a demandé de détailler notre projet et souhaite se laisser le temps pour étudier la faisabilité de notre projet, nos expériences, ainsi que d'avoir un retour de sa hiérarchie et du responsable de l'UE (Vincent DUPUIS) → nous sommes très déçus de ne pas avoir pu manipuler ce jour, surtout que la deadline fixée à fin mars se rapproche, nous étions en accord avec nos plannings initiaux mais cela va nous faire perdre (facilement) une semaine pour des motifs déraisonnés pour l'utilisation d'une soufflerie simple en milieu surveillé → mesure prise: commencer la partie numérique à la place et revoir notre protocole expérimental pour aller à l'essentiel, c'est à dire mesures, données expérimentales lors du créneau futur dédié pour être efficace et rattraper un retard que nous envisagions pas, nous effectuerons les analyses après ! Approximations numériques: utilisation de Python, modules numpy et matplotplib.pyplot pour tracer des lignes de courant, compréhension des fonctions numpy.meshgrid et matplotlib.pyplot.quiver pour tracer des vecteurs (sous forme locale comme des gradients) dans le cas du cube Problème rencontré: la figure obtenue ne correspond pas à la réalité physique, dans mon repère (x,y) mes vecteurs pointent vers l'origine (0,0) avec croissance à l'infini alors qu'ils devraient partir horizontalement puis éviter le cube (traînée) → erreur dans la fonction donnant la force de traînée et de dérive, ou alors mauvaise utilisation du repère (x,y) → corrections à apporter pour la prochaine fois —- === 03/03/17 === (Enzo - 1H00) Modèle numérique: corrections apportés au modèle, passer de valeurs discrètes à continues pour augmenter le rendu final sur le graph (c'est à dire passer de vecteurs à un plan (x,y) en échelle de couleurs progressives), colorisation avec la méthode np.hypot (affecte une valeur à la différence vecteurs termes à termes, cette même valeur qui est code une couleur précise) —- === 04/03/17 === (Enzo - 2H00) Modèle numérique: contrairement au premier modèle simple établi (modulation des coordonnées localement par la force en présence sur chaque point), on réalise un second modèle, suivant les équations de Navier-Stokes, un modèle qui se rapproche davantage des méthodes de computation de dynamique des fluides numérique → définition de la structure général du code, notamment des fonctions exprimant la pression et les vitesses locales, mais il me reste encore à tenir compte de la force aérodynamique dans mon modèle Problème rencontré: il me faut obtenir les équations de Navier-Stokes, les comprendre, les exprimer en un système de coordonnées utiles dans notre cas (cartésien manifestement) puis les discrétiser pour en faire une résolution numérique (équations différentielles non linéaires !) —- === 05/03/17 === (Hector - 0H30) Lecture d'article, sur le corps d'Ahmed, modèle simplifié de coupe de voiture, c'est un cube arrondi avec a l'arrière un aileron, en bougeant cet aileron on peut voir des variation sur les turbulences. —- === 07/03/17 === (Enzo - 2H00) Modèle numérique: Le code avance bien, j'ai réussi à intégrer ma force aérodynamique F=(Fx,Fy) avec le modèle déterminé théoriquement, de plus j'ai relié ça aux vecteurs vitesses V=(u,v) (selon x et y) → problème: il reste juste à déterminer la surface de référence pour la F1 et la voiture, puis à intégrer ça au code, de plus le résultat attendu n'est pas pleinement satisfaisant je dois apporter des corrections sur mes vitesses aux limites Expérience: j'ai pu rencontrer à nouveau le technicien du cinquième étage de l'Atrium, je lui ai fourni une plaquette sur l'expérience désirée ; nous pourrions réaliser un montage en mesurant le “souffle” par mesure de la tension aux bornes de la soufflerie, puis effectuer une analyse de pointage avec Cineris pour déterminer nos valeurs expérimentales de F pour déterminer les coefficients C (surtout celui de traînée Cx) ; nous avons aussi communiqué sur nos disponibilités par mail —- === 08/03/17 === (Enzo - 2H00) Numérique: Suite au dernier problème, je devais apporter des corrections à mon modèle des vitesses : j'ai essayé de refaire entièrement la définition de mes vecteurs vitesses par incrémentations successives → ce modèle ne semble pas donner de résultats concluants. Je retourne donc au modèle précédent et j'intègre des conditions initiales sur mes matrices u,v de taille (nx,ny) idéalement prises carrées. Le résultat semble mieux mais je pense tomber sur la partie arrière de mon expérience (après l'objet), je dois donc définir un champ de vecteurs avant (identiques selon x, rien sur y) puis pendant le passage autour du cube (nul dans le cube et fonction au dessus-dessous) —- === 09/03/17 === (Anthony - 2H00) J'ai pu réaliser la plupart du diagramme de Gantt (rétrospectif) en prenant en compte tous les problèmes rencontrés durant la durée du projet : le reste sera à finir lors de l'aboutissement du projet. J'ai également trouvé un site afin de rédiger l'article en LaTeX ; je me suis familiarisé avec l'interface et je commencerai la rédaction demain. (Christophe - 2H00) Recherches bibliographiques supplémentaires en vue des expériences à venir et de la rédaction de l'article. Approfondissement des notions de traînées, déportances et résistance de l'air. Estimation de différentes valeurs de résistance de l'air pour nos maquettes ayant un coefficient de traînée connu. Estimation des maîtres couples pour nos différentes maquettes. Découverte de 2 souffleries numériques, pouvant être utile ultérieurement pour comparer nos résultats obtenus numériquement. — ===10/03/17=== (Anthony - 1H00) Outline de l'article en mettant les points nécessaires pour la rédaction de l'introduction et des autres parties de l'article (bibliographie, méthodologie, etc…) — ===13/03/17=== (Enzo) Contact avec l'encadrante pour faire le point sur les avancées, les problèmes et pour définir un autre rendez-vous pédagogique — ===15/03/17=== (Anthony - 1H30) J'ai commencé à rédiger la partie théorique de la synthèse du projet afin de bien tout expliquer ; les équations et concepts utilisés afin d'aboutir à modéliser notre expérience et évaluer les résultats de manière cohérente. (Enzo - 2H00) Wiki: rédaction de la partie d'approximations numériques, insertion de formules mathématiques sur le wiki, travail de finition sur le code en intégrant une fonction de surface qui est dynamique avec la position — ===16/03/17=== (Enzo - 2H00) Modélisation numérique: le code est enfin fini et opérationnel, les figures sont extraites et mises en ligne sur le wiki, les explications sont complétées, le détail du code aussi Expérience: nous avons eu une réponse des techniciens de l'Atrium, nous allons pouvoir manipuler le mercredi 22/03 après-midi — ===17/03/17 === (Christophe - 2H00) Découverte et utilisation du logiciel JavaFoil permettant une étude détaillé des caractéristiques aérodynamiques selon le profil de l'objet étudié : calcul de la portance, traînée, déportance et visualisation de l'écoulement pour plusieurs formes élémentaires ( cubes, sphère et profils NACA ) Application à la formule 1 complexe, étant donné que le logiciel est essentiellement utilisé dans le domaine de l'aviation ( la base de donnée proposer à ce sujet est d'ailleurs impressionnante, plus de 1500 profils proposés par l'UIUC ), mais possible. — === 18/03/17 === (Christophe - 3H30) Finalisation des calculs via JavaFoil. Wiki : Première ébauche de la seconde approche de notre partie numérique. A compléter dans les jours à venir. — === 19/03/17 === (Enzo - 1H00) Wiki: travail sur la mise en page, ajout de détails sur la partie numérique (première approche), corrections — === 20/03/17 === (Enzo - 0H30) Retour de l'encadrante, ajout d'informations sur la partie théorique — === 22/03/17 === (Enzo, Anthony, Christophe, Hector - 4H00) Expérience: nous avons enfin pu manipuler en Atrium 504, nous avons réalisé notre manipulation à l'aide de nos maquettes, d'une caméra, du logiciel Cinéris, etc… Nous avons mesuré la masse des maquettes et nous avons pointé sur chaque image un point fixe du cube pour obtenir sa position à chaque instant. De là, nous avons établi un bilan des forces et nous avons exporté nos résultats (t,x,y) sous forme d'un tableau Excel pour traitement des données et interprétations ultérieures. — === 24/03/2017 === (Christophe - 1H00) Finalisation de la partie numérique (Enzo, Anthony - 0H30) Entretien avec l'encadrante: échange sur les détails de la journée de présentation, sur la vidéo, sur l'article, point sur les tâches effectuées jusqu'à maintenant — === 27/03/17 === (Enzo - 1H00) Rédaction du wiki: partie expérimentale avec situation expérimentale et illustrations mathématiques, il nous manque des croquis et les études numériques — === 28/03/17 === (Enzo - 2H00) Poursuite du wiki: traitement des données, premières courbes pour déterminer l'accélération mesurée, établissement du modèle, cas concrets du cube et de la voiture il ne restera plus qu'à affirmer les résultats et préciser les conclusions — === 29/03/17 === (Anthony, Enzo - 3H00 ) Application des concepts, détermination de Cx: ceci a été fait grâce aux courbes et également grâce aux concepts théoriques appris lors du projet. Application numérique faite également. Comparaisons. Mise en page Contact avec l'encadrante pour prendre un rendez-vous après les vacances de Pâques — === 30/03/17 === (Enzo, Anthony - 4H00) Wiki: partie théorique et numérique vérifiées et complètes, diagramme de Gantt rétrospectif, partie expérimentale - surfaces de références indiquées, lien entre puissance et vitesse, il reste finalement à indiquer les incertitudes, à faire les applications numériques et à vérifier l'orthographe — === 31/03/17 === (Enzo - 2H00) Clôture du wiki: finalisation, dernières vérifications (Anthony - 3H00) Applications numériques, vérifications d'orthographe; vérifications de raisonnement ===== Synthèse du projet ===== Cette partie est ici pour mettre en ordre nos idées, afin de les exposer clairement de manière rigoureuse et propre. Elle condense toutes nos recherches afin de proposer une synthèse concise et précise de notre étude. — ==== Partie théorique ==== Avant de se lancer dans les expériences diverses de notre projet, nous nous devons de bien assimiler les notions théoriques que l'aérodynamisme implique, que ce soit mathématiquement ou physiquement. — === Données numériques === Vitesse maximale atteignable par une Formule 1: $V_{F1} = 366,1 ~km.h^{-1}$ (chiffre donné par la Fédération Internationale de l'Automobile - FIA) Vitesse du son dans l'air: $c_{son}=340 ~m.s^{-1}$ Longueur de la Formule 1: $L_{F1} \simeq 3,40 ~m$ === Calculs préliminaires: informations sur le fluide === On se place dans les conditions de Mach et de Reynolds adéquates correspondant à notre cadre théorique. On considère donc un fluide incompressible sec, ici l'air. On assimile l'air à un gaz parfait. Naturellement, ce gaz suit la loi des gaz parfaits: $$P V = n R T$$ avec $P$ la pression du gaz, $V$ son volume, $n$ le nombre de moles le constituant, $T$ sa température et $R$ la constante des gaz parfaits. On donne $R = 8,3144621 ~J.mol^{-1}.K^{-1}$. Pour faire apparaître la masse volumique $\rho$ de l'air, on fait la fait apparaître en posant: $$\rho = \frac{m}{V} \Rightarrow V= \frac{m}{\rho}$$ En injectant cette donnée dans notre loi des gaz parfaits, on obtient, en remarquant que la masse molaire du gaz s'écrit $M=\frac{n}{m}$: $$P \frac{m}{\rho} = n R T \Rightarrow \rho = \frac{P M}{R T}$$ On fait notre application numérique en prenant $P_{atm}=10^{5} ~Pa$, $M_{air}=28,9 ~g.mol^{-1}$ et $T=293,15 ~K$: nous trouvons $\rho_{air}=1,19 ~kg.m^{-3}$. Son incertitude associée est donnée par les valeurs $\Delta P = 1 ~Pa, \Delta M = 0,1 ~g.mol^{-1}, \Delta T = 1 ~K$ et par la formule: $$\Delta \rho_{air} = \rho_{air} \sqrt{(\frac{\Delta P}{P})^2+(\frac{\Delta M}{M})^2+(\frac{\Delta T}{T})^2} \Rightarrow AN: \Delta \rho_{air} = 5,9.10^{-3} ~kg.m^{-3}$$ Par la suite, on considère la valeur référence $\rho_{air}=1,204 ~kg.m^{-3}$ proche de notre résultat et nous ne considérerons pas d'incertitude dessus. On définit le coefficient de viscosité cinématique $\nu$ par l'expression: $$\nu = \frac{\mu}{\rho}$$ avec $\mu$ le coefficient de viscosité dynamique en $Pa.s$ et $\rho$ la masse volumique du fluide en $kg.m^{-3}$. On se donne $\mu = 1,80.10^{-5} ~Pa.s$. Ainsi, l'application numérique donne $\nu = 1,50.10^{-5} ~m^{2}.s^{-1}$. On ne considère par d'incertitude sur cette valeur. — Tout d’abord, différencions les différents types d'écoulement et d'aérodynamisme. Pour cela, nous nous aiderons de deux nombres a-dimensionnées: le nombre de Reynolds et le nombre de Mach. === Écoulements === Les types d’écoulement dépendent du nombre de Reynolds donné par la formule : $$Re=\frac{V L}{\nu}$$ avec $V$ la vitesse caractéristique du fluide en $m.s^{-1}$, $L$ la dimension caractéristique en $m$ et $\nu$ la viscosité cinématique du fluide en $m.s^{-2}$. Ainsi, quatre régimes apparaissent: * régime de Stokes ($Re<1$) * régime laminaire ($Re \simeq 1$) * régime transitoire ($Re \simeq 2300$) * régime turbulent ($Re \simeq 3000$) Toutes ses valeurs sont indicatives et sont sujettes à varier selon le profil du corps et de nombreux autres paramètres externes. En appliquant cette formule dans notre cas, nous pouvons faire les applications numériques nécessaires. On suppose que la vitesse (de nature vectorielle) du fluide est l'opposé (vectoriel) de la vitesse de la Formule 1. Ainsi, les normes de ces vitesses sont égales donc $V_{fluide}=V_{F1}$. La dimension caractéristique du problème est la longueur $L_{F1}$ de la Formule 1. Ainsi, nous obtenons $Re_{max} \simeq 2.10^{7}$, ce qui implique que nous nous trouvons dans le cas du régime turbulent. === Aérodynamisme === Les types aérodynamisme dépendent du nombre de Mach qui est donné par la formule suivante: $$ Ma = \frac{v}{c} $$ On peut ensuite diviser le résultat numérique en plusieurs cas: * régime incompressible ($Ma<0,2$) * régime subsonique ($0,2<Ma<1$) * régime transsonique ($1<Ma<Ma\_{crit}$) * régime supersonique ($Ma_{crit}<Ma<5$) Le régime transsonique représente une valeur de la vitesse très légèrement supérieure à la vitesse du son. Les deux derniers cas ne nous intéresseront pas car la Formule 1 ne peut pas aller à une telle vitesse. Faisons les applications numériques: $Ma_{max} \simeq 0,28$ ce qui implique que nous nous plaçons dans le régime incompressible. === Forces aérodynamiques === Ensuite, intéressons nous aux différentes forces s’exprimant sur le corps en mouvement d'un point de vue aérodynamique: $$\vec{F_i} = \frac{1}{2} \rho \vec{V_i}^2 S_{ref} [C_i] \vec{e_i}$$ avec $\vec{e_i}$ un vecteur de la base canonique de $\mathbb{R} ^3$. La force selon $\vec{e_x}$ s'appelle la traînée, elle est opposée au mouvement du fluide donc est dans la direction opposée au mouvement de la voiture. La dérive est la force selon $\vec{e_y}$ et la portance est selon $\vec{e_z}$ La traînée s’oppose au mouvement du fluide donc dans la direction opposée au mouvement de la voiture. Cette force s’exerce sur le module de façon perpendiculaire au mouvement. === Équation de Navier-Stokes === Afin de modéliser l'expérience de façon numérique, nous nous sommes également aidé de l’équation de Navier-Stokes: $$\rho \left ( \frac{\partial{u}}{\partial{t}}+(u \dot{} \nabla u) \right )=-\nabla P + \mu \nabla ^2 u$$ avec $u$ le champ de vitesse, $P$ la pression, $\rho$ la masse volumique du fluide et $\mu$ sa viscosité. Cette formule importante décrit le mouvement d'un fluide en considérant les forces de pression et les forces visqueuses. ==== Approche expérimentale ==== Toute approche fondamentale ne peut avoir de poids sans une validation et une comparaison entre la théorie et l'expérience, la pensée et la pratique. Dans cette section, nous mettons justement en lumière notre vision expérimentale de notre étude. — === Situation expérimentale === Le but de cette manipulation est de déterminer les coefficients de traînée pour différents types de structure et de les comparer à des tables déjà établies. Cela est une manière de mettre à l'épreuve nos résultats théoriques et numériques et, dans le cas où nous rencontrons un obstacle, de corriger notre modèle. On réalise le montage suivant:

  

  Figure 1 - Schématisation de l'expérience

  On se place dans le référentiel du laboratoire que l'on suppose inertiel. On considère le système {module} de masse $m$, que l'on suppose uniforme et continu. On se donne un repère de base $\left\{\vec{e_x}, \vec{e_y}, \vec{e_z} \right\}$ ainsi qu'une horloge d'origine $t=0$. On considère l'accélération de la pesanteur à Paris soit $g=9,81 ~m.s^{-2}$ On réalise un bilan des forces qui s'exercent sur le module: nous avons tout d'abord le poids $\vec{P}$ du module ainsi que la réaction $\vec{N}$ du support, toutes deux portés selon $\vec{e_z}$. Ensuite, nous considérons la force de frottement cinétique uniquement $\vec{f_{cin}}$ selon $\vec{e_x}$; en effet, on réalise nos mesures dès que le mobile commence à bouger et donc seuls les frottements cinétiques entrent en jeu et non les frottements statiques.

  

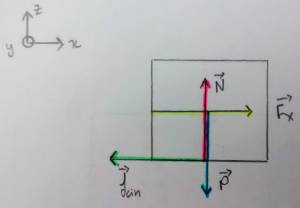
  Figure 2 - Représentation du bilan des forces exercée sur le module

  Par le principe fondamental de la dynamique, nous avons: $$\sum\nolimits_{i} \vec{F_i} = m \vec{a} \Rightarrow \vec{P} + \vec{N} + \vec{F} + \vec{f_{cin}} = m \vec{a} \Rightarrow \vec{F} + \vec{f_{cin}} = m \vec{a} \Rightarrow \vec{F} = m \vec{a}- \vec{f_{cin}}$$ On regarde le mouvement selon $\vec{e_x}$ uniquement, car on suppose aucun mouvement selon $y$ ce qui est vrai en pratique, la dérive étant extrêmement faible dû aux rails: $$F_x = m a_{mes} + f_{cin}$$ En détaillant notre force de frottement, on a, sachant que la réaction du support compense le poids du module: $$||\vec{f_{cin}}|| = \mu_c ||\vec{N}|| \Rightarrow f_{cin} = \mu_c ||\vec{P}|| \Rightarrow f_{cin} = \mu_c m g$$ Notre $\mu_c$ est le coefficient de frottement dynamique entre nos deux surfaces, ici du plexiglas et du plasique PLA. En regardant dans des tables de valeurs, on donne $\mu_c=0,3$. En remplaçant notre expression de la force aérodynamique de traînée par notre résultat théorique, nous avons: $$\frac{1}{2} \rho V^2 S_{ref} C_x = m a_{mes} + \mu_c m g$$ $$C_x = \frac{2 m(a_{mes} + \mu_c g)}{\rho V^2 S_{ref}}$$ Avant toute chose, on vérifie notre résultat en faisant une analyse dimensionnelle: $\rho V^2 S_{ref}$ à la dimension d'une force $M.L.T^{-2}$ donc $C_x$ est a-dimensionné ce qui est correct. Puissance du souffle, détermination de la vitesse Soit la puissance électrique $P=U I$ avec $U$ et $I$ étant la tension en $V$ et l'intensité en $A$. L'intensité mesurée est $I=1,1 ~A$ avec $\delta I=0,1 ~A$. On suppose que lors de la transformation de l'énergie électrique en énergie mécanique (rotation des pales), il n'y a aucune perte énergétique. Ainsi en définissant la puissance d'une force, on a $P=\vec{F} \dot{} \vec{V}$ soit dans notre cas où $\vec{F}$ et $\vec{V}$ sont colinéaires, $V=\frac{P}{F}$ avec $F$ la force totale $F=F_x + f_{cin}$ et $V$ la vitesse de l'air. Ceci nous aidera à déterminer la puissance donnée de la soufflerie à l'air. On utilisera ensuite $P=F V$ afin de calculer la vitesse de l'air soufflé (ce qui donne la vitesse de l'objet car on assimile $V_{obj} = V_{air}$ Cependant la vitesse obtenue ici est la vitesse de l'air. Afin d'obtenir $V$ du fluide présent dans la formule de la force de traînée, on effectue: $$V=V_{air}- \left < V_{objet} \right > _t $$ En utilisant cette idée et en la comnbinant avec notre modèle quadratique de la position, on obtient: $$V = \frac{ U I - (\alpha \left < t \right > _t + \beta) F}{F}$$ === Protocole expérimental === On propose ici d'étudier la force de traînée pour différents objets afin de pouvoir mettre en évidence le coefficient de traînée $C_x$. Nous avons donc besoin de calculer la force de traînée, nous proposons ainsi une expérience permettant de calculer cette force. Matériel pour l'expérience * 3 maquettes: un cube, une Formule 1, une voiture (imprimées en 3D via la PMClab) * Rail et support * Balance * Souffleur d'air * Caméra * Logiciel de traitement vidéo: Cinéris Manipulations * On pèse les maquettes pour déterminer leurs masses. * On place une maquette sur le support encadré par les rails, on place le souffleur en face. * On active le souffleur dont les pales tournent à une vitesse V donnée fonction de la tension à ses bornes. * On enregistre les mouvements de la maquette sur le rail avec la caméra. * Avec notre logiciel Cinéris, on trace la position de l'objet en fonction du temps: on donne pour cela une échelle (tant de centimètres réels correspondent à tant de pixels sur l'image) * On dérive cette courbe pour obtenir la vitesse et une seconde fois pour avoir l’accélération voulue: comme nos résultats ne sont pas parfaits, nous allons modéliser nos données (une certaine fonction linéaire, une parabole, une hyperbole, etc…) === Analyse et incertitudes === Toute manipulation réelle implique des sources (différentes) d'incertitudes possibles lors des nos recherches. Ainsi, nous prendrons en compte les incertitudes suivantes: * $\Delta U = 10~V$, incertitude dû au graduation pour faire varier la puissance du souffleur * $\Delta t = 0,03~s, \Delta x = 0,01~m$, incertitude faite par Cinéris * $\Delta m = 0,1~g$, incertitude de la balance * $\Delta l = 0,5~cm$, incertitude de mesures de longueurs caractéristiques des maquettes On réalise ainsi nos mesures, nos manipulations et obtenons des séries de données $[t,x(t),y(t)]$. Nous faisons l'approximation de regarder le mouvement selon $x$ et donc nous ne considérerons pas les mouvements sur $y$ (qui en pratique sont très faible, surtout causées par les erreurs de pointage). On décide de modéliser nos données par une fonction $f$ de paramètre $t$ polynomiale de degré 2. En effet, on souhaite avoir une information sur l'accélération du système qui est nécessairement différente de zéro dans notre cas vu que le module avance. Plus précisément: $$f(t)=\alpha t + \beta ,~(\alpha,\beta) \in \mathbb{R}^2 \Rightarrow \frac{d^2 f(t)}{d t^2} = 0$$ $$f(t)=\alpha t^2 + \beta t + \gamma ,~(\alpha,\beta,\gamma) \in \mathbb{R}^3 \Rightarrow \frac{d^2 f(t)}{d t^2} = 2 \alpha$$ Ainsi, avec notre modèle, notre accélération sera égale à $a_{mes}=2 \alpha$, où $\alpha$ est le coefficient quadratique de notre modèle. La dimension du coefficient $\alpha$ correspond bien à une accélération $M.L.T^{-2}$. De plus, en considérant ce modèle parabolique, nous avons une information sur la vitesse de l'objet nécessaire pour estimer la vitesse du fluide; en effet: $$\frac{d f (t)}{d t} = 2 \alpha t + \beta$$ En considérant la moyenne temporelle, nous avons $ \left < V_{objet} (t) \right > _t = 2 \alpha \left < t \right > _t + \beta $, cette formule nous sera utile dans l'expression de la vitesse du fluide. Cas du cube Données expérimentales: $m_{cube} = 125,2 ~g,~U_{cube}=200~V,~l_{cube}= 7,8~cm$

  

  Figure 3 - Présentation des résultats expérimentaux dans le cas du cube

  Estimation de la surface de référence Dans le cas du cube, on rappelle que la surface de référence (qui fait face au flux d'air) est donnée par $S_{ref} = l^2$ avec $l$ le côté du cube. Ainsi, $$S_{ref} = l_{cube} ^2 \Rightarrow \Delta S_{ref} = 2 S_{ref} \frac{\Delta l_{cube}}{l_{cube}}$$ $$AN: S_{ref} = 60,84 ~cm^2 ,~\Delta S_{ref} = 7,8 ~cm^2$$ Calcul du coefficient de traînée Par lecture graphique, nous avons $\alpha \simeq 0,017 ~m.s^{-2}$ soit en injectant ce résultat dans notre expression de $C_x$: $$C_x = \frac{2 m_{cube}(2 \alpha + g \mu_c)}{\rho_{air} V^2 {l_{cube}}^2 } \Rightarrow AN: C_x = 0,81$$ Cas de la voiture Données expérimentales: $m_{v} = 40,3 ~g,~U_{v}=250 ~V,~ L_{pb} =3,5 ~cm,~ l_{pb} =3,0 ~cm,~ L_{pc} =4,6 ~cm,~ l_{pc} =1,4 ~cm,~ h=2,0 ~cm$

  

  Figure 4 - Présentation des résultats expérimentaux dans le cas de la voiture

  Estimation de la surface de référence La détermination de la surface de référence est plus complexe que dans le cas du cube simple. On regarde toujours la surface en contact frontal avec l'air: nous devons donc regarder la voiture de face. On décompose cette surface de référence en deux sous-surfaces. La première étant le pare-choc avant de la voiture qui n'est autre qu'un rectangle de largueur $l_{pc}$ et de longueur $L_{pc}$ donc $S_1= l_{pc} L_{pc}$ $AN: S_1= 7,7 ~cm^2$. La deuxième surface de référence est le pare-brise: $S_2 = \frac{1}{2} (l_{pb} + L_{pb}) h sin{\theta}$ avec $\theta$ l'angle entre le pare-brise et le vent incident et les dimensions du pare-brise et cette surface est assimilée à un trapèze. $AN: S_2 = 4,1 ~cm^2$ Évidemment, on ajoute ces deux surfaces afin d'obtenir la surface de référence totale: $$S=S_1 + S_2 \Rightarrow \Delta S = \Delta S_1 + \Delta S_2$$ Notre incertitude sur les surfaces sont égales et valent $\Delta S_1=\Delta S_2=0.1 ~cm^2$. $$AN: S=11,8 ~cm^2, \Delta S = 0,2 ~cm^2$$ Calcul du coefficient de traînée Par lecture graphique, nous avons $\alpha \simeq 0,012 ~m.s^{-2}$ soit en injectant ce résultat dans notre expression de $C_x$: $$C_x = \frac{2 m_{voiture}(2 \alpha + g \mu_c)}{\rho_{air} V^2 S_{voiture} } \Rightarrow AN: C_x =0,65 $$ Cas de la Formule 1 Données expérimentales: $m_{F1} = 20,5 ~g,~U_{F1}=250 ~V, ~L_n =3.7 ~cm,~ l_n =0.4 ~cm,~ L_m =2.5 ~cm,~ l_m = 0.5~cm,~ \phi = 15°,~h=0.5~cm,~R=0.55~cm,~ l_d = 0.5~cm,~ L_d =1.0 ~cm,~ l_s = 0.5~cm,~ L_s = 0.5~cm$

  

  Figure 5 - Présentation des résultats expérimentaux dans le cas de la Formule 1

  Estimation de la surface de référence La surface de référence fut plus compliquée à déterminer car il fallait décomposer la Formule 1 selon une multitude de surfaces avec des angles d'inclinaison qui varient selon la position de la Formule 1. Nous avons noté sept surfaces: Surface 1: nez de la Formule 1 La surface est rectangulaire donc $S_1= l_n L_n$ $AN: S_1=1,4 ~cm^2$ Surface 2: museau de la Formule 1 La surface peut être assimilée à un rectangle avec une courbure de $\phi$ que l'on approxime comme constante; $S_2= l_m L_m sin{\phi} $ $AN: $S_2= 0,35 ~cm^2$ Surface 3: roues avant Pour une seule roue, on a utilisé les coordonnées cylindriques afin de calculer sa surface de référence. On a assimilé la roue à un cylindre et en arrêtant notre intégration sur $\theta$ à $\pi$ car la moitié de la roue est 'percutée' par le vent incident et $e$ est l'épaisseur de la roue et $R$ son rayon; d'où $S_3= R e \pi$ $AN: 2 S_3= 1,7 ~cm^2$ Surface 4: déflecteurs Cette surface est un rectangle très légèrement incurvé, si petit que l'on ignore ce terme (car $cos{\theta}=1$ quand $\theta$ tend vers $0$). Ainsi, $S_4= l_d L_d $ $AN: 2 S_4= 1 ~cm^2$ Surface 5: siège du pilote Le siège est encore un rectangle ce qui donne $S_5= l_s L_s $ $AN: S_5= 0,25 ~cm^2$ Surface 6: roues arrières On a utilisé les coordonnées cylindriques afin de calculer sa surface de référence. On a assimilé la roue à un cylindre et en arrêtant notre intégration sur $\theta$ à $\frac{\pi}{2}$ car seulement un quart de la roue est 'percuté' par le vent incident et $e$ est l'épaisseur de la roue et $R$ son rayon; d'où $S_6= \frac{\pi}{2} R e$ $AN: S_6= 0,87 ~cm^2$ Surface 7: aileron La largeur de l'aileron est si infime et l'aileron est si bien protégée par le reste de la Formule 1 (l'aileron n'est pas aussi imposant que pour les Formule 1 à taille réelle) que cette surface est négligeable par rapport aux autres; soit $S_7 = 0$. La surface de référence totale est obtenue en sommant nos surfaces découpées. L'avantage avec cette méthode est que l'on obtient la surface de chacune des pièces de la Formule 1 et est assez proche de la réalité; cependant cette méthode nécessitait également quelques approximations à faire car nous n'avions pas la valeur théorique de la surface de référence. Naturellement; $$S_{F1} = \sum{_{j=1}^{7} {S_j}} \Rightarrow \Delta S_{F1} = \sum{_{j=1}^{7} {\Delta S_j}}$$ $$AN: S_{F1} = 5,57 ~cm^2, \Delta S_{F1}= 0,6 ~cm^2 $$ Calcul du coefficient de traînée Par lecture graphique, nous avons $\alpha \simeq 0,045 ~m.s^{-2}$ soit en injectant ce résultat dans notre expression de $C_x$: $$C_x = \frac{2 m_{F1}(2 \alpha + g \mu_c)}{\rho_{air} V^2 S_{F1} } \Rightarrow AN: C_x = 0,23 $$ === Résultats et interprétations === Notre expérience bien que simple et nécessitant peu de matériel, se retrouve être assez approximative. En effet, énormément d'incertitudes rentrent en jeu si bien que la confiance en notre résultat reste faible. Cela nous semble logique, en effet, même si nous essayons de minimiser nos pertes en abritant le dispositif expérimental, nous ne pourrons atteindre des résultats professionnels. Également, nous avons dû utiliser plusieurs approximations qui s'ajoutent aux incertitudes de l'expérience. Une des plus grosses approximations faites fut que nous avons considéré que la puissance apportée par le moteur de la soufflerie était identique à la puissance de l'hélice de la soufflerie. Cependant, il y a, en réalité, une dissipation d'énergie; ceci affecte la vitesse produite par l'hélice et donc le coefficient de traînée. Nous sommes conscients que ceci apporte une grande incertitude que nous n'avons pas les moyens de quantifier; mais nous n'avions aucun moyen de mesurer la perte de puissance et donc la vraie vitesse produite par l'hélice. Cela illustre bien le fait que le travail d’ingénierie derrière toute étude automobile par exemple est très difficile et que le matériel et les moyens derrière les expérimentations sont très poussés (machine de calcul très puissante, soufflerie gigantesque, logiciels complets, très lourds et très coûteux, etc…). ==== Modélisation numérique ==== On se propose ici d'établir un modèle numérique de nos flux d'air autour de nos modules. Deux approches seront considérées: l'une à l'aide d'un code réalisé par nos soins et l'autre utilisant des programmes déjà établis par des universitaires. — === Première approche: code Python réalisé par les étudiants du projet === Partons des équations de Navier-Stokes établies dans la partie théorique: $$\frac{\partial u}{\partial t}+u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}=-\frac{1}{\rho}\frac{\partial p}{\partial x}+\nu\left(\frac{\partial^2 u}{\partial x^2}+\frac{\partial^2 u}{\partial y^2}\right)+F_x$$ $$\frac{\partial v}{\partial t}+u\frac{\partial v}{\partial x}+v\frac{\partial v}{\partial y}=-\frac{1}{\rho}\frac{\partial p}{\partial y}+\nu\left(\frac{\partial^2 v}{\partial x^2}+\frac{\partial^2 v}{\partial y^2}\right)+F_y$$ $$\frac{\partial^2 p}{\partial x^2}+\frac{\partial^2 p}{\partial y^2}=-\rho\left(\frac{\partial u}{\partial x}\frac{\partial u}{\partial x}+2\frac{\partial u}{\partial y}\frac{\partial v}{\partial x}+\frac{\partial v}{\partial y}\frac{\partial v}{\partial y}\right)$$ avec $\rho$ la masse volumique, $p$ la pression, $\nu$ le coefficient de viscosité cinématique et $(u,v)$ le champ de vecteurs considéré. On décide alors de poser notre force aérodynamique $\vec{F}$ comme: $$F_x = \frac{1}{2} \rho _{air} S V^2 C_x ,~ F_y = \frac{1}{2} \rho _{air} S V^2 C_y$$ Remarque: Nous considérons ici une force $\vec{F}$ selon les directions $x$ et $y$ uniquement. Ainsi, nous réaliserons une représentation des lignes de courant dans le plan $(x,y)$ ; seulement rajouter une troisième dimension reviendrait à considérer également une force $F_z$ selon $z$ comme la force de portance incluant déjà la correction du poids du module lors du bilan des forces. $$F_z = \frac{1}{2} \rho _{air} S V^2 C_z - m g$$ On réalise alors un processus d'Euler, c'est-à-dire que l'on va approcher la solution de notre système différentiel en discrétisant nos valeurs à l'aide d'un certain pas. On pose alors la discrétisation suivante (de même pour les coordonnées spatiales): $$\frac{\partial A}{\partial t} \simeq \frac{A_{n}-A_{n-1}}{\Delta{t}}$$ Ainsi, en utilisant ceci dans nos équations de Navier-Stokes, nous trouvons: $$u_{i,j}^{n+1} = u_{i,j}^{n} - u_{i,j}^{n}\frac{\Delta t}{\Delta x}(u_{i,j}^{n}-u_{i-1,j}^{n})-v_{i,j}^{n}\frac{\Delta t}{\Delta y}(u_{i,j}^{n}-u_{i,j-1}^{n})-\frac{\Delta t}{\rho 2\Delta x}(p_{i+1,j}^{n}-p_{i-1,j}^{n})+\nu\left[\frac{\Delta t}{\Delta x^2}(u_{i+1,j}^{n}-2u_{i,j}^{n}+u_{i-1,j}^{n})\right.+\left.\frac{\Delta t}{\Delta y^2}(u_{i,j+1}^{n}-2u_{i,j}^{n}+u_{i,j-1}^{n})\right] + F_x \Delta t$$ $$v_{i,j}^{n+1}=v_{i,j}^{n} - u_{i,j}^{n}\frac{\Delta t}{\Delta x}(v_{i,j}^{n}-v_{i-1,j}^{n})-v_{i,j}^{n}\frac{\Delta t}{\Delta y}(v_{i,j}^{n}-v_{i,j-1}^{n})-\frac{\Delta t}{\rho 2\Delta y}(p_{i,j+1}^{n}-p_{i,j-1}^{n})+\nu\left[\frac{\Delta t}{\Delta x^2}(v_{i+1,j}^{n}-2v_{i,j}^{n}+v_{i-1,j}^{n})\right.+\left.\frac{\Delta t}{\Delta y^2}(v_{i,j+1}^{n}-2v_{i,j}^{n}+v_{i,j-1}^{n})\right]+F_y \Delta{t}$$ $$p_{i,j}^{n} = \frac{(p_{i+1,j}^{n}+p_{i-1,j}^{n})\Delta y^2+(p_{i,j+1}^{n}+p_{i,j-1}^{n})\Delta x^2}{2(\Delta x^2+\Delta y^2)}-\frac{\rho\Delta x^2\Delta y^2}{2(\Delta x^2+\Delta y^2)}\times\left[\frac{1}{\Delta t}\left(\frac{u_{i+1,j}-u_{i-1,j}}{2\Delta x}+\frac{v_{i,j+1}-v_{i,j-1}}{2\Delta y}\right)- \frac{u_{i+1,j}-u_{i-1,j}}{2\Delta x}\frac{u_{i+1,j}-u_{i-1,j}}{2\Delta x} \right.- 2\frac{u_{i,j+1}-u_{i,j-1}}{2\Delta y}\frac{v_{i+1,j}-v_{i-1,j}}{2\Delta x}-\left.\frac{v_{i,j+1}-v_{i,j-1}}{2\Delta y}\frac{v_{i,j+1}-v_{i,j-1}}{2\Delta y}\right]$$ On remarque ainsi que le vecteur de pression est directement donné par des opérations sur le champ de vecteurs alors que les composantes de $u$ et de $v$ sont définies à partir d'un schéma d'Euler donc pour un rang $n+1$. Cela implique que nous allons devoir préciser une série de valeurs initiales pour $u$ et $v$. On choisira d'utiliser le langage Python (en version 3) pour sa simplicité d'utilisation et nous nous aiderons des modules /numpy/ et /matplotlib.pyplot/ qui servent respectivement à manipuler des tableaux et à tracer en courbes. Pour nous faciliter la tâche, on crée des fonctions pour la définir la pression, les forces et la surface de référence pour travailler plus facilement au sein de la boucle où nous avons juste à implémenter nos opérations sur les matrices $u$ et $v$. On discrétise notre espace en une matrice que l'on préférera carré de taille $n_x \times n_y$ (donc avec $n_x=n_y$). <code> #définition de la pression de Poisson def pressure(p,u,v,rho,dx,dy,dt,n_time): pn=np.empty(np.shape(p)) #on crée une matrice similaire à p for k in range(n_time): pn = p.copy() #copie p pour faire des opérations dessus #intérieur du tableau p[1:-1, 1:-1] = ¹⁾