Equation de noeuds sur OpenScad

Description

Introduction

Noeuds

Noeuds toriques / torus knots

Modélisation dans OpenScad

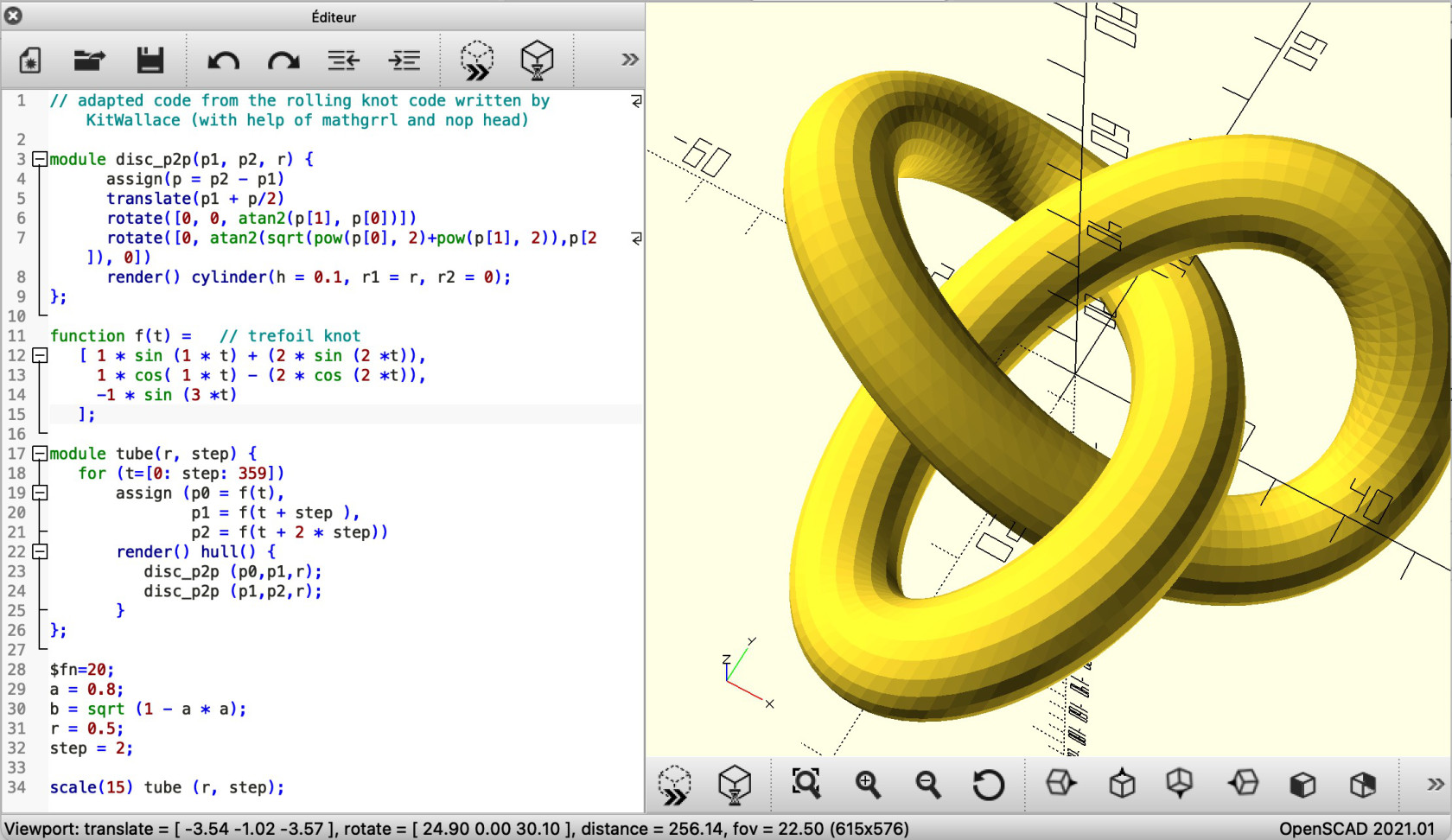
Méthode de hulling et exemple du rolling knot

 

 

 

Equation d'un trefoil knot

J'ai commencé à chercher le nœud torique le plus simple que je puisse faire, qui est aussi le nœud non trivial le plus simple. Vous souvenez-vous duquel il s'agit ? Oui, c'est le nœud de trèfle, également désigné comme le noeud torique (2,3). J'ai trouvé ces équations pour la première fois sur la page du trefoil knot de Wikipedia :

Je me suis d'abord concentrée sur les premières équations paramétriques données, et j'ai remplacé la fonction f(t) dans mon exemple OpenSCAD précédent de 'rolling knot' par celles-ci. Cela a fonctionné ! Et voilà, mon premier trefoil knot dans OpenSCAD.

Généralisation à tous les noeuds toriques

Nous voulons maintenant généraliser ce que nous venons d'expérimenter avec un nœud tréflé à tous les nœuds torses.

Rappelons la définition des nœuds de tore donnée par Wikipedia :

En théorie des nœuds, un nœud de tore est un type particulier de nœud qui se trouve sur la surface d'un tore non noué dans R3. [...] Chaque nœud de tore est spécifié par une paire d'entiers coprimes p et q. [...]

La notation (p,q)-torus est une convention, mais il en existe une où vous trouverez la définition inverse de p et q ! A certains endroits, le même noeud peut être appelé T(3,2) et à d'autres endroits (2,3). C'est très déroutant. Je continue avec la convention utilisée ci-dessus et dans le livre de Seager.

Voici ce que Wikipédia nous apprend sur leurs représentations géométriques :

Le nœud (p,q)-tore s'enroule q fois autour d'un cercle à l'intérieur du tore, et p fois autour de son axe de symétrie de rotation. Si p et q ne sont pas relativement premiers, nous avons un lien de tore avec plus d'une composante. La direction dans laquelle les brins du nœud s'enroulent autour du tore est également sujette à différentes conventions. La plus courante consiste à faire en sorte que les brins forment une vis à droite pour p q > 0.

Cela semble être un très bon début. Nous pouvons étendre ces équations à d'autres tores avec des dimensions paramétriques, en considérant les tores suivants :

le tore est à symétrie azimutale par rapport à l'axe z
c est le rayon entre le centre du trou et le centre du tube du tore
a est le rayon du tube
nous n'avons considéré que les tores en anneau (c>a)
En écrivant les équations cartésiennes d'un tel tore, on peut alors obtenir les équations énoncées dans le blog Wolfram Mathworld :

Equation d'un tore en utilisant les coordonnées cartésiennes : (c-sqrt(x^2+y^2))^2+z^2=a^2   

Les équations paramétriques sont donc :

x   =   (c+acosv)cosu   
y   =   (c+acosv)sinu   
z   =   asinv   
pour u,v dans [0,2pi]. 

Pour revenir à notre nœud torique, nous pouvons finalement obtenir une description paramétrique du nœud torique (p,q) sous la forme d'une fonction f(t), en fixant u = q*t et v=p*t, pour t dans [0,2pi]. Cela nous donne :

c=10;// rayon entre le centre du trou et le centre du tube
a=6; // rayon du tube (c>a pour un anneau torique)
p=2; // tore (p,q) dans la notation où (p<q)
q=3; // tore (p,q)  dans la notation où (p<q)

function f(t) =   
[ (c+(a*cos(q*t)))*cos(p*t),
(c+ (a*cos(q*t)))*sin(p*t),
(a*(sin(q*t)))
];

Nous sommes prêts à utiliser cette description paramétrique avec les solutions de hulling de KitWallace. Notez que comme OpenSCAD semble ne pas prendre en compte les radiants mais seulement les degrés, il faut itérer sur t allant de 0 à 359, et non de 0 à 2*pi.

Code OpenScad

Voici donc un code permettant de modéliser un noeud (p,q)  dans OpenSCAD :

// Clara Devanz - Fabacademy 2023
// Closely adapted code from the rolling knot code written by KitWallace (who also credits mathgrrl and nop head), but with knot torus parametric equations : https://mathworld.wolfram.com/Torus.html
// Here the notation where q > p is used. Thus q is the number of times the knot cross the center of the torus and p is the number ot times it turns around the z-axis.
//  The torus is azimuthally symmetric about the z-axis; c is the radius from the center of the hole to the center of the torus tube, and a is the radius of the tube. We considered only ring tori (c>a).

// Here are the parameters you're invited to modify!

p=2; // (p,q) torus
q=3; // (p,q) torus
c=10; // radius from the center of the hole to the center of the tube
a=6; // radius of the tube
r = 2; // radius of the knot
step = 1; // steps of the 'for' loop calculating the knot's sections for t=[0: step: 359])
$fn=50; // number of fragments. Will change the 

function f(t) =   
[ (c+(a*cos(q*t)))*cos(p*t),
(c+ (a*cos(q*t)))*sin(p*t),
(a*(sin(q*t)))
];

module disc_p2p(p1, p2, r) {
      assign(p = p2 - p1)
      translate(p1 + p/2)
      rotate([0, 0, atan2(p[1], p[0])])
      rotate([0, atan2(sqrt(pow(p[0], 2)+pow(p[1], 2)),p[2]), 0])
      render() cylinder(h = 0.1, r1 = r, r2 = 0);
};

module tube(r, step) {
   for (t=[0: step: 359])
       assign (p0 = f(t), 
               p1 = f(t + step ),
              p2 = f(t + 2 * step))
       render() hull() {
          disc_p2p (p0,p1,r);
          disc_p2p (p1,p2,r);   
       }
};

scale(2) color([0.968,0.788,0.961]) tube (r, step);

 

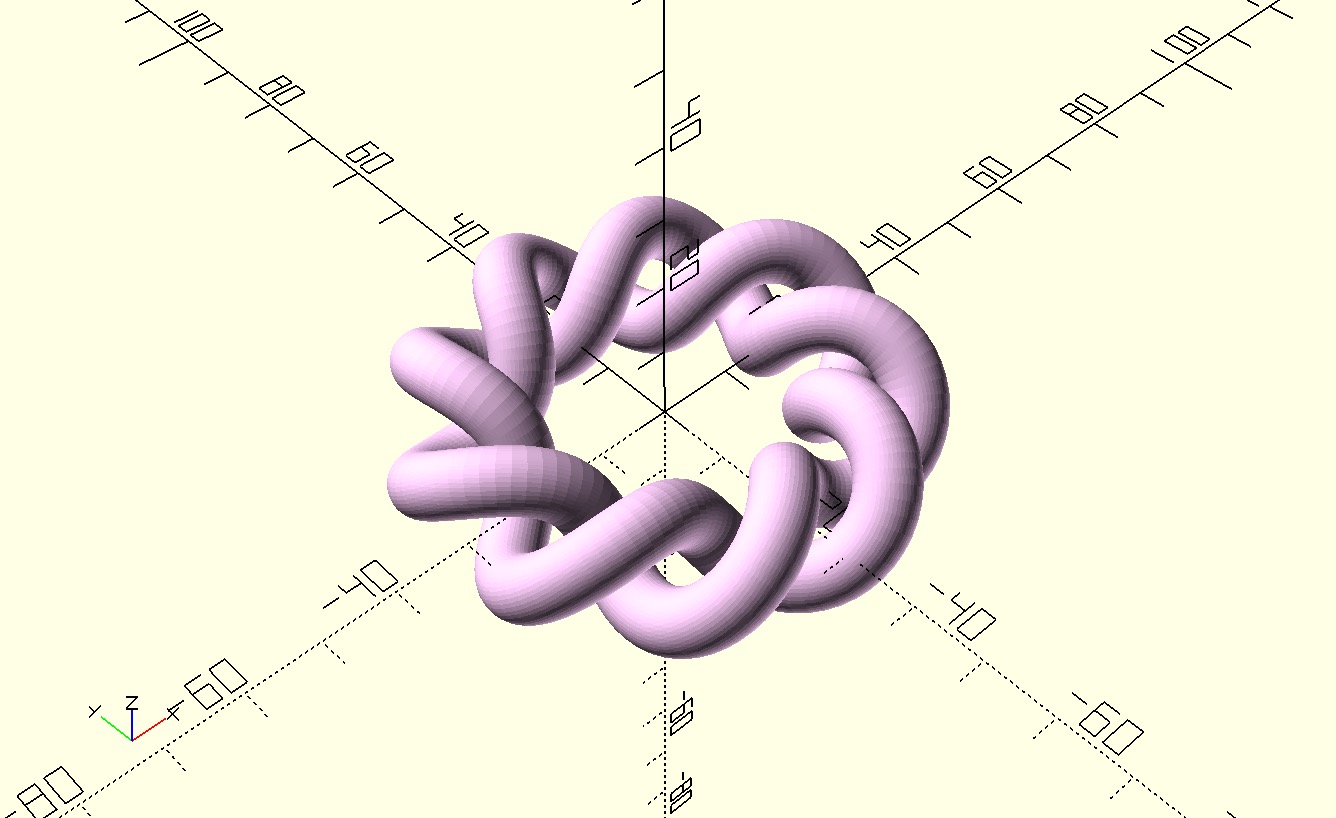
Ce qui donne le résultat suivant :

J'aime beaucoup cette description paramétrique, la forme me semble plus réussie que le premier essai !

Vous pouvez voir dans le code qu'en plus des paramètres de la fonction paramétrique, nous pouvons également modifier certains paramètres de simulation. Enfin, voici la liste de tous les paramètres avec lesquels vous êtes invités à jouer :

• p et q caractérisent le tore (p,q) sur lequel vous tracez votre nœud, dans la convention où p < q.
• c est le rayon entre le centre du trou et le centre du "tube" du tore
• a est le rayon du "tube" du tore (c>a pour un tore annulaire)
• r est le rayon de la section de votre tube de nœud
• step est la valeur des pas sur lesquels la boucle 'for' itère pour calculer les sections du nœud for t=[0 : step : 359])
• $fn est le nombre de fragments utilisés pour le calcul de la surface à travers la section du noeud

Je n'ai pas pris le temps d'analyser toutes les parties du code concernant le hulling mais au moins je peux vraiment jouer avec les paramètres maintenant !

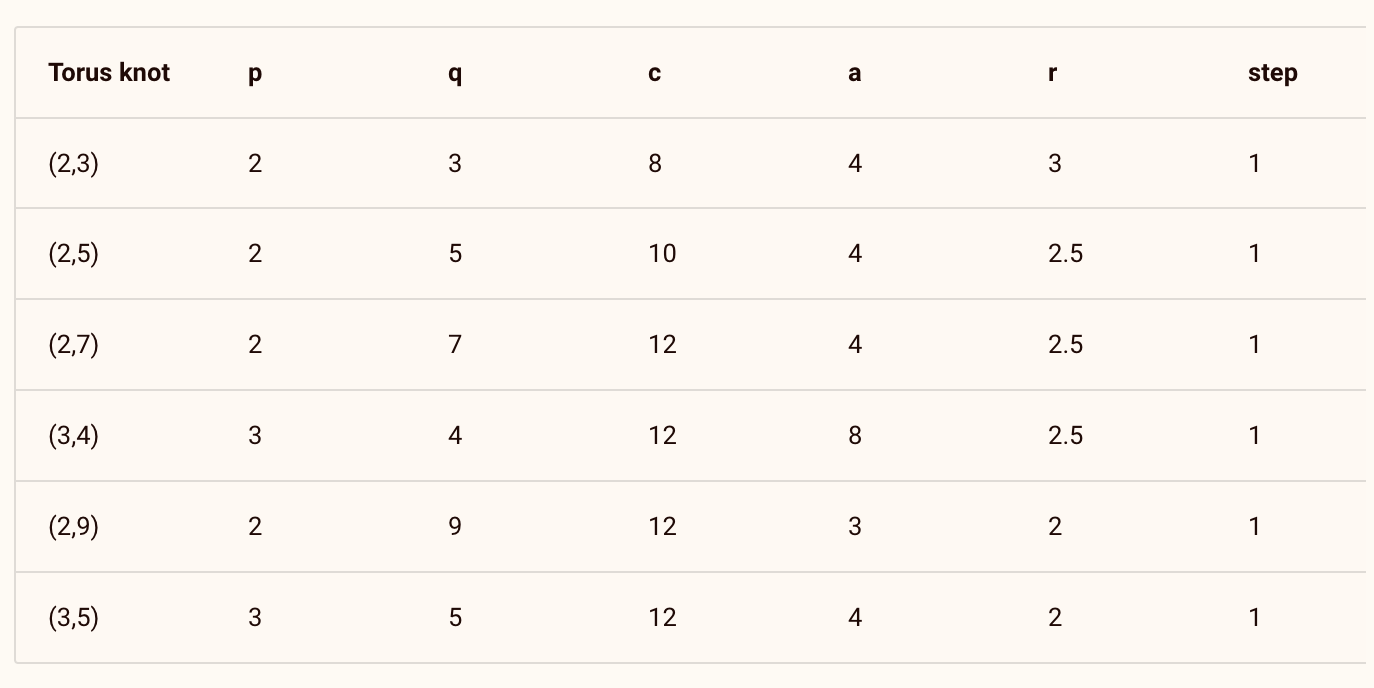
Illustrations de noeuds modélisés

Voici quelques nœuds toriques que j'ai rendus avec les paramètres suivants :