Equation de noeuds sur OpenScad
Description
Introduction
Auteure du tutoriel : Clara Devanz
Il y a quelques temps, un ami m'a offert un livre fascinant d'Henry Segerman intitulé Visualizing Mathematics with 3D Printing. J'ai découvert cet ouvrage en ligne grâce au riche site web qui l'accompagne, 3dprintmath.com. Certains modèles sont même disponibles à l'impression sur Thingiverse ! Le livre donne plus d'explications sur les figures et la théorie, de façon accessible aux débutant·es.
Pendant la Fabacademy, il était demandé aux apprenant·es de modéliser et imprimer des formes difficiles voire impossibles à réaliser autrement qu'avec la fabrication additive. J'ai repensé à certaines formes expliquées dans le livre de Segerman, et tout particulièrement aux noeuds toriques.
Puisqu'il s'agît de visualiser des concepts mathématiquement bien définis, le logiciel de modélisation le plus adéquat m'a semblé être OpenScad. Ce logiciel libre permet en effet de décrire des volumes à partir d'équations. Je n'avais pas d'expérience préalable sur ce logiciel, c'est pourquoi je vous invite à me signaler en commentaire de cette page si vous voyez de meilleures façons de procéder ou des imprécisions. De même, si des grosses erreurs en topologie se sont glissées ici, ce n'est pas du tout un champ que je connais bien.
Voici le résultat obtenu après modélisation et impression de quelques noeuds toriques :
Noeuds
En mathématiques, et plus particulièrement en géométrie et en topologie algébrique, un nœud est un plongement d'un cercle dans ℝ3, l'espace euclidien de dimension 3, considéré à des déformations continues près. Une différence essentielle entre les nœuds usuels et les nœuds mathématiques est que ces derniers sont fermés (sans extrémités permettant de les nouer ou de les dénouer) ; les propriétés physiques des nœuds réels, telles que la friction ou l'épaisseur des cordes, sont généralement également négligées. [Wikipedia]
Mais encore ? Eh bien voici une vidéo tout à fait pédagogique de Carlo H. Séquin :
Noeuds toriques
Un noeud est torique s’il peut se réaliser à la surface du tore de révolution. Autrement dit, ceux-ci sont obtenus en enroulant un fil autour d'un tore en tournant p fois autour de l'anneau et effectuant q tours complets, où p et q sont des entiers premiers entre eux .
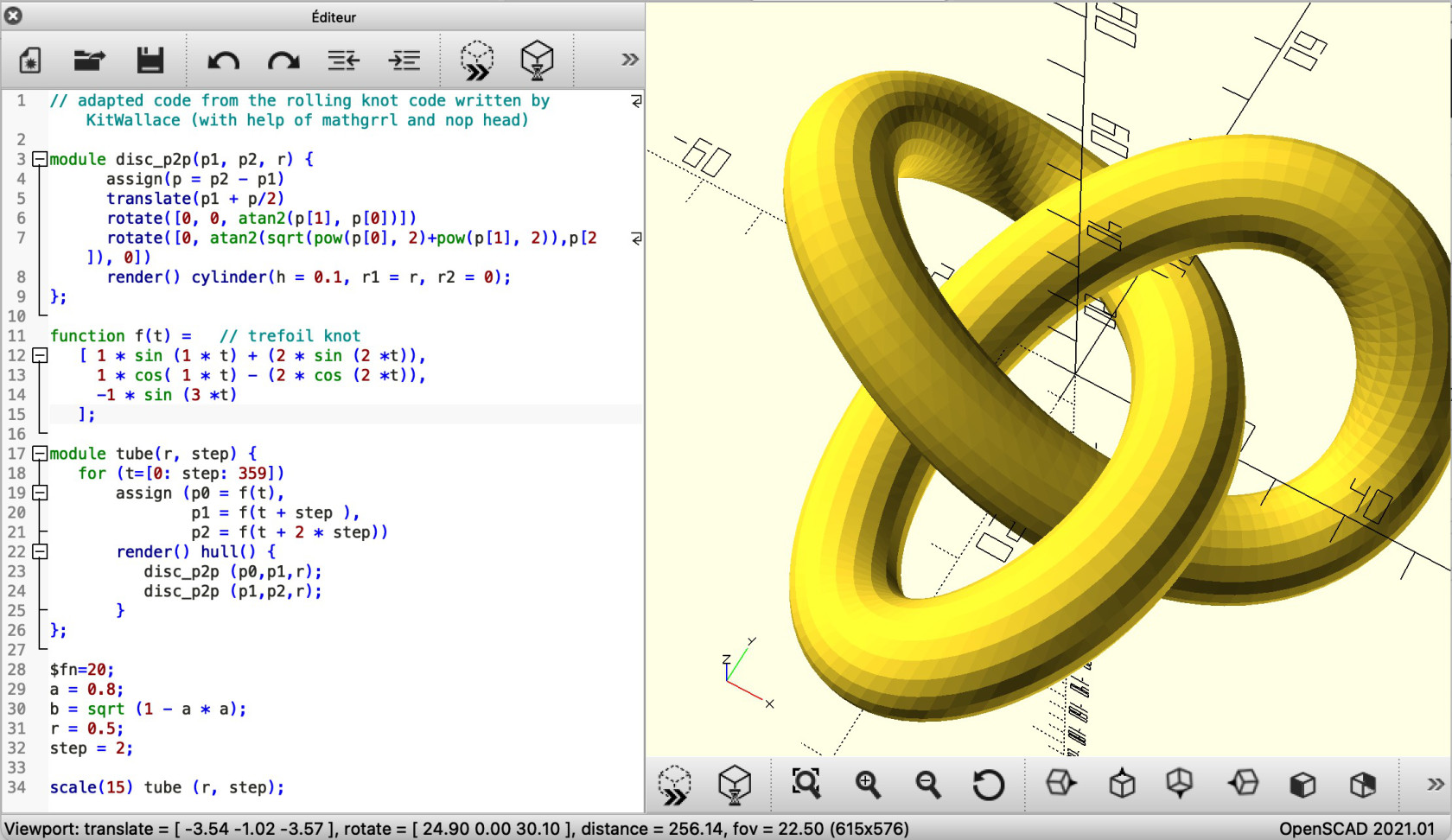
Par exemple le noeud de trèfle illustré ci-dessus fait deux fois le tour du tore dans la direction des parallèles pendant qu’il fait trois fois le tour dans la direction des méridiens. C'est le noeud torique (2,3). [source image]
Modélisation dans OpenScad
Méthode de hulling et exemple du noeud roulant
Equation d'un noeud de trèfle
J'ai commencé par chercher à cherchermodéliser le nœud torique le plus simple que je puisse faire,simple, qui est aussi le nœud non trivial le plus simple. Il s'agit du nœud de trèfle,fle, également désigné comme le noeud torique (2,3). J'ai trouvé ces équations pour la première fois sur la page anglophone du noeud de trèfle (trefoil knot) de Wikipedia :
Je me suis d'abord concentrée sur les premières équations paramétriques données, et j'ai remplacé la fonction f(t) dans mon exemple OpenSCAD précédent de 'rolling knot' par celles-ci. Cela a fonctionné ! Et voilà, mon premier noeud de trèfle modélisé dans OpenSCAD.
Généralisation à tous les noeuds toriques
Nous voulons maintenant généraliser ce que nous venons d'expérimenter avec un nœud de trèfle à tous les nœuds toriques
Rappelons la définition des nœuds torique donnée par Wikipedia :
En théorie des nœuds, un nœud torique est un type particulier de nœud qui se trouve sur la surface d'un tore non noué dans R3. [...] Chaque nœud de tore est spécifié par une paire d'entiers coprimes p et q. [...]
La notation (p,q)-torus est une convention, mais il en existe une où vous trouverez la définition inverse de p et q ! A certains endroits, le même noeud peut être appelé T(3,2) et à d'autres endroits (2,3). C'est très déroutant. Je continue avec la convention utilisée ci-dessus et dans le livre de Seager.toriques.
Voici celes queéquations Wikipédia nous apprend sur leurs représentations géoméparamétriques :
Cela semble être un très bon début. Nous pouvons étendre ces équations à d'autres tores avec des dimensions paramétriques,tores, en considérant les tores suivants :
- le tore est à symétrie azimutale par rapport à l'axe z
- c est le rayon entre le centre du trou et le centre du tube du tore
- a est le rayon du tube
- nous
n'avonsconsidéronsconsidéré queuniquement les tores en anneau (c>a)
En écrivant les équations cartésiennes d'un tel tore, on peut alors obtenir les équations énoncées dans le blog Wolfram Mathworld :
Equation d'un tore en utilisant les coordonnées cartésiennes : (c-sqrt(x^2+y^2))^2+z^2=a^2
Les équations paramétriques sont donc :
x = (c+acosv)cosu
y = (c+acosv)sinu
z = asinv
pour u,v dans [0,2pi]. Pour revenir à notre nœud torique, nous pouvons finalement obtenir une description paramétrique du nœud torique (p,q) sous la forme d'une fonction f(t), en fixant u = q*t et v=p*t, pour t dans [0,2pi]. Cela nous donne :
c=10;// rayon entre le centre du trou et le centre du tube
a=6; // rayon du tube (c>a pour un anneau torique)
p=2; // tore (p,q) dans la notation où (p<q)
q=3; // tore (p,q) dans la notation où (p<q)
function f(t) =
[ (c+(a*cos(q*t)))*cos(p*t),
(c+ (a*cos(q*t)))*sin(p*t),
(a*(sin(q*t)))
];Nous sommes prêts à utiliser cette description paramétrique avec les solutions de hulling de KitWallace. Notez que comme OpenSCAD semble ne pas prendre en compte les radiants mais seulement les degrés, il faut itérer sur t allant de 0 à 359, et non de 0 à 2*pi.
Code OpenScad
Voici donc un code permettant de modéliser un noeud (p,q) dans OpenSCAD :
// Clara Devanz - Fabacademy 2023
// Closely adapted code from the rolling knot code written by KitWallace (who also credits mathgrrl and nop head), but with knot torus parametric equations : https://mathworld.wolfram.com/Torus.html
// Here the notation where q > p is used. Thus q is the number of times the knot cross the center of the torus and p is the number ot times it turns around the z-axis.
// The torus is azimuthally symmetric about the z-axis; c is the radius from the center of the hole to the center of the torus tube, and a is the radius of the tube. We considered only ring tori (c>a).
// Here are the parameters you're invited to modify!
p=2; // (p,q) torus
q=3; // (p,q) torus
c=10; // radius from the center of the hole to the center of the tube
a=6; // radius of the tube
r = 2; // radius of the knot
step = 1; // steps of the 'for' loop calculating the knot's sections for t=[0: step: 359])
$fn=50; // number of fragments. Will change the
function f(t) =
[ (c+(a*cos(q*t)))*cos(p*t),
(c+ (a*cos(q*t)))*sin(p*t),
(a*(sin(q*t)))
];
module disc_p2p(p1, p2, r) {
assign(p = p2 - p1)
translate(p1 + p/2)
rotate([0, 0, atan2(p[1], p[0])])
rotate([0, atan2(sqrt(pow(p[0], 2)+pow(p[1], 2)),p[2]), 0])
render() cylinder(h = 0.1, r1 = r, r2 = 0);
};
module tube(r, step) {
for (t=[0: step: 359])
assign (p0 = f(t),
p1 = f(t + step ),
p2 = f(t + 2 * step))
render() hull() {
disc_p2p (p0,p1,r);
disc_p2p (p1,p2,r);
}
};
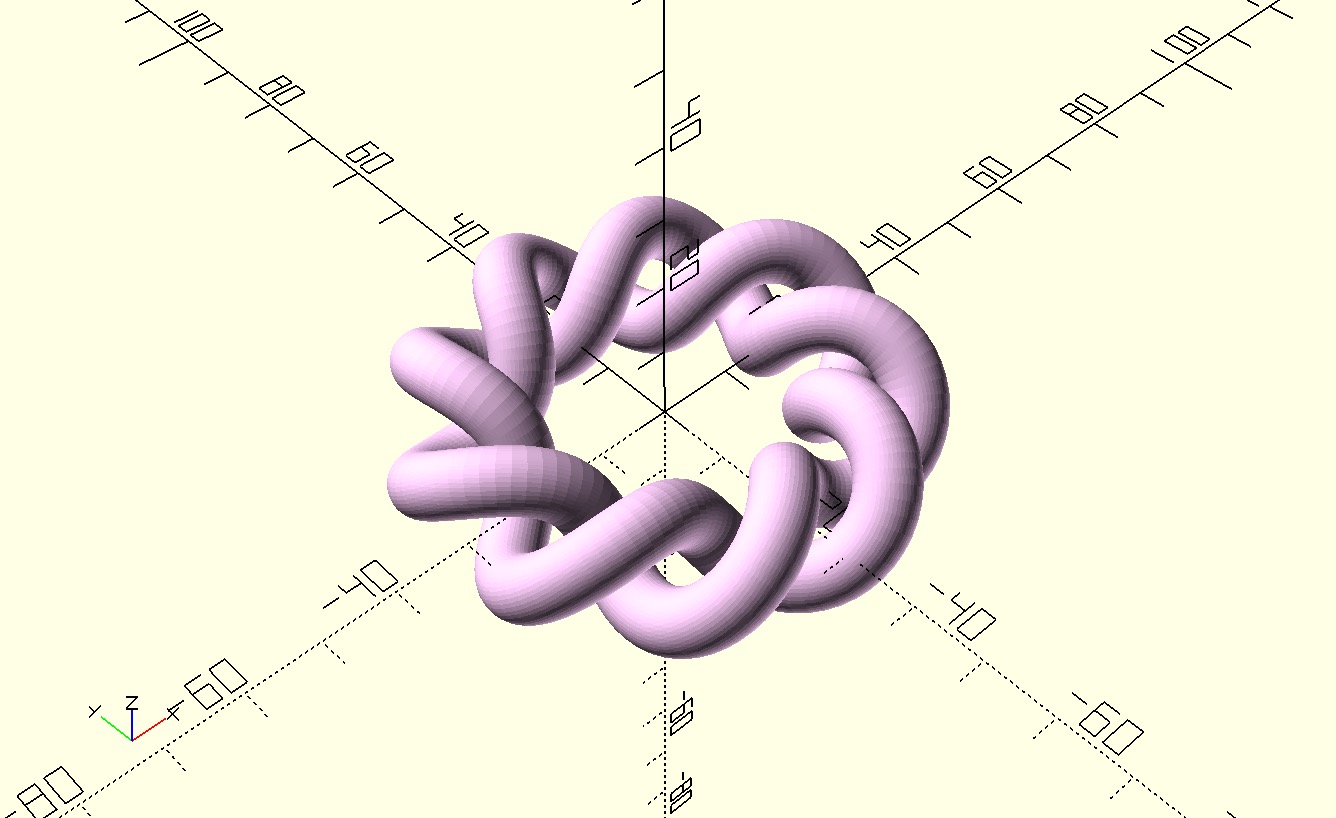
scale(2) color([0.968,0.788,0.961]) tube (r, step);Ce qui donne le résultat suivant :
J'aime beaucoup cette description paramétrique, la forme me semble plus réussie que le premier essai !
Vous pouvez voir dans le code qu'en plus des paramètres de la fonction paramétrique, nous pouvons également modifier certains paramètres de simulation. Enfin,Voici doncvoici la liste de tous les paramètres avec lesquels vous êtes invités à jouerexpérimenter :
- p et q caractérisent le tore (p,q) sur lequel vous tracez votre nœud, dans la convention où p < q.
- c est le rayon entre le centre du trou et le centre du "tube" du tore
- a est le rayon du "tube" du tore (c>a pour un tore annulaire)
- r est le rayon de la section
de votredu tubede nœud - step est la valeur des pas sur lesquels la boucle 'for' itère pour calculer les sections du nœud
forpour t=[0 : step : 359]) - $fn est le nombre de fragments utilisés pour le calcul de la surface à travers la section du noeud
Je n'ai pas pris le temps d'analyser toutes les parties du code concernant le hulling mais au moins je peux vraiment jouer avec les paramètres maintenant !
Illustrations de noeuds modélisés
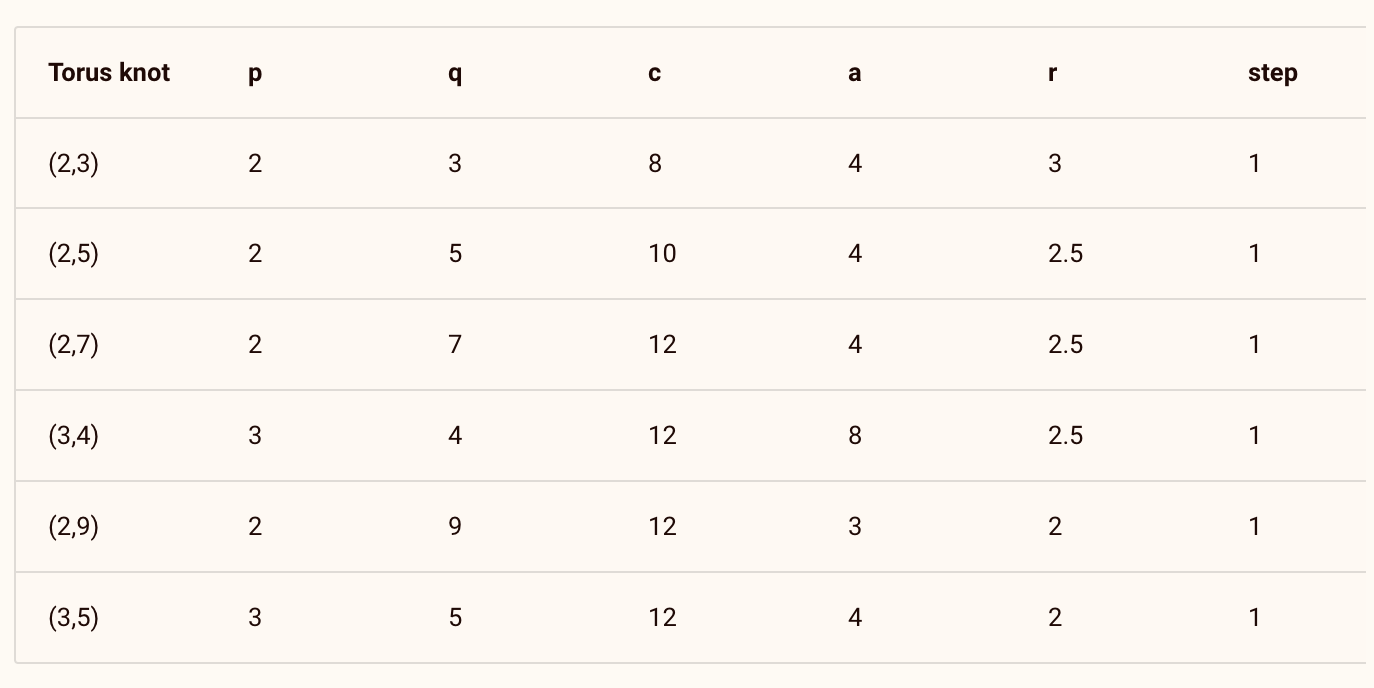
Voici quelques nœuds toriques que j'ai rendus avec les paramètres suivants :
Impression des noeuds
Export en stl
Afin d'imprimer nos dessins en 3D, nous devons les exporter sous forme de fichiers .stl. Dans OpenSCAD, vous devez d'abord rendre votre modèle à l'aide de l'option render. C'est à ce moment-là que le logiciel effectue tous les calculs.
Ouvrez la console OpenSCAD pour vérifier quand il a terminé, car cela peut prendre de longues minutes ! Mes modèles ont mis entre 10 et 20 minutes à être générés (je n'ai pas mesuré le temps avec précision).
Quand c'est bon, vous devriez avoir un message similaire dans votre console :
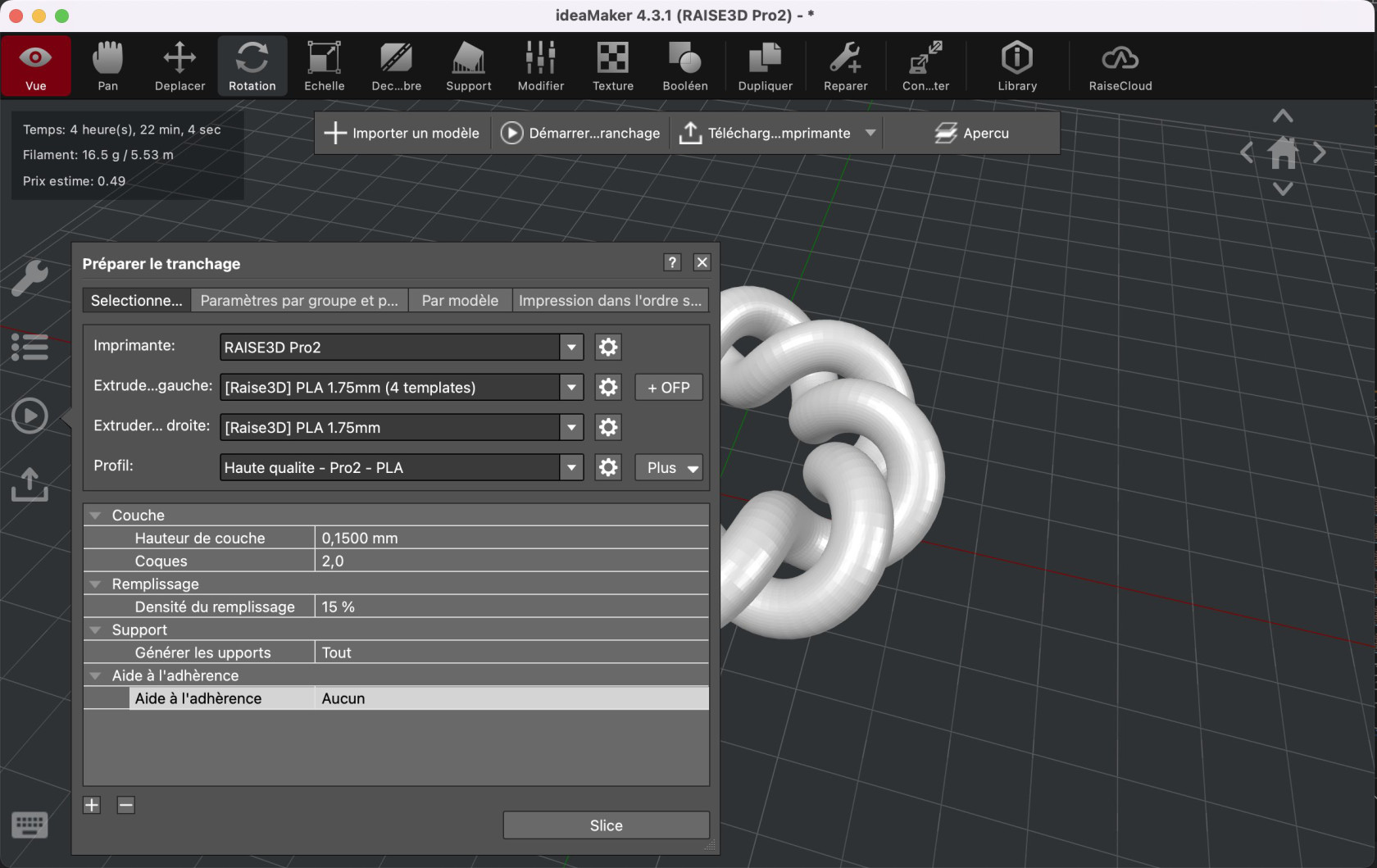
Slicer
Comme d'habitude, j'ai utilisé le slicer ideamaker pour des impressions sur les Raise 3D Pro 2, en filament PLA d'une part, ABS d'autre part.