EMRiver
Modèle analogique d'un système fluviatile: trouver un sable accessible
Lola Asensio, Jade Montagne
Introduction
Dans le cadre de cette UE, notre but était de modéliser un cours d'eau afin d’illustrer l'effet du tri des particules dans un système laminaire, pour rendre le phénomène accessible aux L1 notamment.
Les points clés à démontrer étaient que l’eau a un rôle important dans le transport des particules, et que le transport dépend de la taille de celles-ci, ce qui va créer un tri granulométrique. Pour rappel, dans la nature, ce sont les plus gros grains qui sédimentent en premier.
Dans ce but, des étudiants de Fablab des années passées avaient tenté d’élaborer un modèle analogique de sable en s’inspirant du projet EMRiver. C’est un projet lancé par une société américaine avec une table et du sable en plastique recyclé recréant les propriétés du quartz et ayant l’avantage d’être coloré selon la taille de ses grains. Ils ont réussi à reproduire l’installation proposée par le projet, en utilisant le substitut de sable vendu par EMRiver.
Le souci, c’est que ce sable coûte très cher, que le dispositif est complexe et trop volumineux… d’où notre problématique, à savoir comment modéliser le transport des grains à moindre coût, dans une maquette simplifiée et diminuée ?
-
I.Pistes et matériel
Nous avons essayé de trouver un moyen de modéliser ce transport sans avoir recours à ces particules tout en y intégrant une différence de coloration selon la granulométrie comme proposé par EMRiver. L'intérêt de cette coloration est qu’elle permet de comprendre que les grains sont plus ou moins bien transportés par le courant en fonction de leur taille. Nous avions alors 2 pistes : ou bien tenter de produire nous-mêmes des particules en recyclant du plastique, ou réessayer d’utiliser du sable naturel. On dit réessayer, parce que nos prédécesseurs avaient fait une tentative mais ils avaient rapidement écarté cette option la jugeant inesthétique.
En dehors du problème de coût, nous pouvons signaler que les particules d’EMRiver ne suivent pas un schéma de sédimentation classique, à savoir que ce sont les plus petits grains qui sédimentent en premier.
C’est pourquoi nous avons décidé de redonner une chance au sable naturel, plus précisément du quartz, parce qu’il ne coûte pas cher, que ses propriétés sont connues et que nous espérons qu’il suive un schéma de sédimentation classique.
Voici brièvement le fonctionnement de la maquette inspirée du travail de nos prédécesseurs :
Nous avons utilisé une bassine de dimension 90 x 60 x 30 cm, en la remplissant de sable sur 54 cm et en laissant 42 cm de vide vers la bonde, afin de conserver une épaisseur de sable de 5 cm, permettant ainsi le tracé d’une rivière.
La maquette fonctionne de la manière suivante :
Il faut placer la bassine sur une table afin de pouvoir disposer en dessous deux bacs, l’un pour la décantation et l’autre pour la pompe, dans lesquels on aura préalablement versé et réparti 6 litres d’eau pour une dizaine de kilogrammes de sable. Il faut faire en sorte que la sortie d’eau soit au-dessus du bac de décantation, et placer dans l’autre bac la pompe reliée à un tuyau lui-même en connexion avec l’arrivée d’eau.
Il faut mettre le sable dans la bassine et le mélanger pour homogénéiser la granulométrie, sans le tasser. Nous avons fait le choix de tracer au préalable un méandre pour guider l’eau, et d’ajouter une pente en mettant une planche de 2,5cm de hauteur du côté de l’arrivée d’eau, sous les 10 premiers centimètres de la bassine.
Sous l’entrée d’eau, nous avons placé un EDU (Energy Dissipator Unit), qui est une pièce qui réceptionne l'eau sortant du bec verseur et diminue son énergie cinétique. Ensuite, il suffit de brancher la pompe au moteur et de le régler à la valeur choisie.
-
II.Méthodes et calculs
Nous voulions que tous nos grains soient transportés par la vitesse maximale applicable à notre cours d’eau, qui correspond à l’arrivée d’eau.
C’est pourquoi nous avons entrepris la démarche suivante :
Nous voulions trouver une vitesse de moteur et une taille de particules adéquates pour assurer un transport laminaire. En effet, il s’agit d’un mouvement ordonné des particules d’un fluide qui permet de considérer que la vitesse du transport est uniforme, même en prenant en compte les changements dûs à la pente ainsi qu’aux forces s’appliquant sur les grains comme la poussée d’Archimède, la gravité et les frottements ayant lieu tout le long du cours d’eau.
Pour ce faire, il nous fallait trouver un débit de transport à la fois suffisant pour un régime laminaire, et à la fois applicable sur notre construction dont la pompe a une puissance limitée. Pour obtenir le débit, il faut multiplier la section de la rivière à la vitesse du fluide.
Après plusieurs essais, nous avons observé que l’eau circulait sans abîmer la pompe à une puissance du moteur de 45. Cette dernière est associée à un débit mesuré de 30 mL/s. En supposant que la rivière obtenue fasse en moyenne 0,5 cm de haut pour 5 cm de large, la section vaut 2,5 cm².
Alors, la vitesse, donc le débit divisé par la section, vaut 12 cm/s.
Pour s’assurer que le régime est laminaire, nous avons besoin du nombre de Reynolds qui permet d’établir la nature du régime. S’il est compris entre 500 et 2000, on pourra considérer que le régime est laminaire.
Pour calculer ce nombre, il faut multiplier la largeur de la rivière par la vitesse du courant, et diviser le tout par la viscosité du fluide, ici l’eau douce. La largeur de notre rivière était d’environ 5 centimètres, et la viscosité du fluide était connue, 0,1 cm²/s.
On a ainsi pu trouver un nombre de Reynolds de 600, donc compris entre 500 et 2000. Le système est bien laminaire.
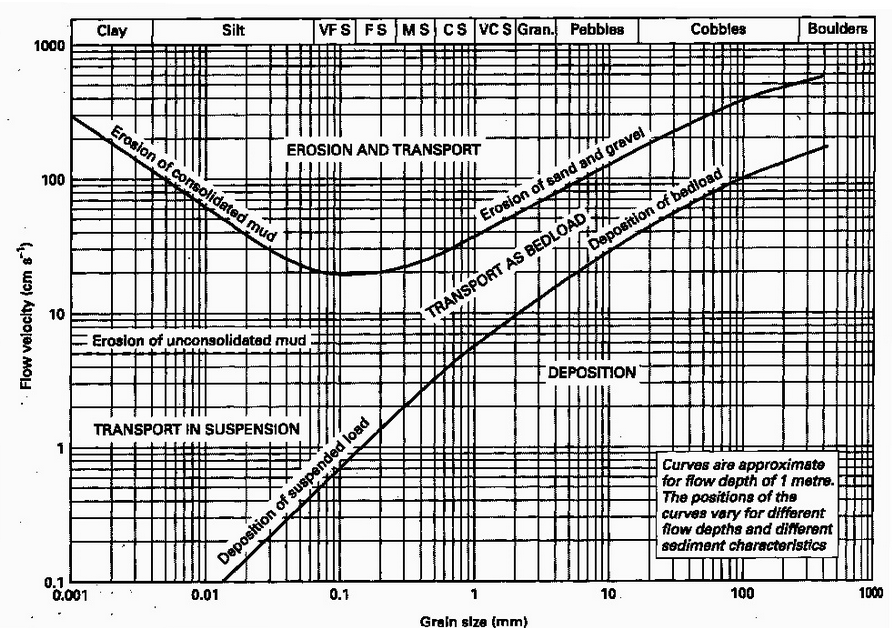
A partir de ces données, nous avons finalement utilisé le diagramme de Hjulstrom pour déterminer la taille de nos grains de quartz. Ce dernier illustre le transport des grains en fonction de la vitesse du fluide. Il montre que plus les grains sont gros, moins ils seront transportés. S’ils sont trop petits, ils restent en suspension. Notre but était d’obtenir une taille moyenne permettant le transport.
Avec cette vitesse de fluide de 12cm/s, nous avons obtenu une taille de particules de sable comprise entre 0,5 mm et 2 mm.
Finalement, pour distinguer les grains selon leur taille, il fallait au moins deux couleurs différentes. Pour ce faire, nous avons fait plusieurs expériences pour colorer le sable. Nous avons aussi cherché du sable naturellement coloré, et avons tamisé beaucoup de sable pour obtenir la granulométrie choisie en quantité suffisante.
-
III.Résultats
Les résultats de nos expériences de coloration nous ont montré que l’encre de Chine et le bleu de méthylène n’étaient pas adaptés. En revanche, nous avons sélectionné un sable d’aquarium vendu comme naturellement coloré qui, il se trouve, s’avérait artificiellement coloré. Il s’est avéré qu’en contact avec de l’acétone, il se décolore. Néanmoins, il fonctionne pour notre expérience, c’est pourquoi nous avons choisi ce sable, de tailles allant de 0,5 à 1mm.
Nous avions un deuxième type de sable, de 1 à 2mm, lui aussi du quartz mais de couleur claire (blanc à marron).
La bassine à notre disposition était noire, ne permettant pas l’observation optimale des grains foncés. Nous l’avons donc colorée en bleu pour créer un contraste avec nos grains.
Nous avons fait plusieurs essais probants : le sable était bien transporté, même si, dans les faits, cette maquette n'illustrant pas pleinement les événements géologiques dans ses dimensions temporelles et spatiales, nous avons à nouveau obtenu ce transport inversé, c’est-à-dire que les petites particules se déposent en premier. En plus de ce transport, nous avons pu observer une érosion au niveau des rives concaves, et la formation de méandres abandonnés et d’un delta.
https://www.youtube.com/watch?v=bq6eCxD2WLE
Conclusion
Pour conclure, avec ce sable naturel, nous obtenons des résultats similaires aux particules du modèle d'EMRiver. Nous pensons donc avoir répondu à la problématique initiale : voilà un sable à la fois peu coûteux, coloré, qui permet de montrer un granoclassement et ce de manière simplifiée et reproductible.
En perspective, pour passer d’une maquette à un réel modèle, il faudrait faire varier un paramètre à la fois et observer les conséquences sur le comportement des grains. Pour cela, on peut facilement faire varier la pente, mais aussi modifier le tracé, comme par exemple la forme du méandre réalisé préalablement, notamment sa longueur d’onde. On peut ajouter de l’eau en début d’expérience qui représenterait la mer en aval du cours d’eau. On peut aussi envisager, même si c’est plus complexe, de faire varier la vitesse maximale de l’eau mais pour cela il vaudrait une pompe plus performante au risque d’être rapidement limités. On peut arriver à un débit maximal de 40mL/s, soit une vitesse de 15cm/s, en restant en régime laminaire. Dans ces conditions, on pourrait faire varier la taille des grains mais en ayant seulement 1mm de plus afin d’assurer un transport selon le diagramme de Hjulstrom. En effet, on ne peut diminuer la taille des grains car quand ils sont plus petits que 0,5mm, ils flottent.
Bibliographie :
1. « Emriver Stream Tables & Hydraulic Flumes ». Emriver, https://emriver.com/.
2. Dodds John, Baluais Gérard. Caractérisation de la taille des particules. Sciences Géologiques. Bulletin, tome 46, n°1-4, 1993. Minéraux finement divisés, sous la direction de Jacques Yvon. pp. 79-104.
3. Miedema, Sape. Dredging Processes, The Loading Process of a Trailing Suction Hopper Dredge. Delft University of Technology. 2012.
4. Kathy Lazard, Amaury Leroy, Dan Rebibo et Alice Saugrain. “Modèle analogique sable”. Wiki des projets de l’UE Fablab. 2022-2023.
https://wiki.fablab.sorbonne-universite.fr/BookStack/books/projets-due-2022-2023/page/modele-analogique-sable
Remerciements :
Nous tenons tout d'abord à remercier Loïc Labrousse pour son apport pédagogique et scientifique, ainsi que Pierre Théry pour sa disponibilité et son savoir-faire. Nous remercions également Laurence Le Callonnec pour son investissement dans l'identification de notre sable.
Carnet de bord :
Afin de rendre accessible le phénomène de sédimentation des rivières, notamment aux L1, notre but est de modéliser un cours d'eau suffisamment élaboré pour illustrer l'effet du tri des particules dans un système laminaire. Les modèles précédents nous permettent de réutiliser un mécanisme efficace pour reproduire le système aquifère. Notre priorité est de trouver un substitut au sable d'EMRiver, qui est très coûteux. Dans le meilleur des cas, nous aimerions avoir un mode de dépôt similaire à la sédimentation naturelle du sable (les grosses particules sédimentent en premier).
L'argument de nos prédécesseurs contre l'utilisation du sable était son manque d'esthétisme. Cependant, il semblerait qu'ils aient comparé le sable non coloré avec le sable vendu par EMRiver, et donc teinté. Nous pouvons essayer de créer du sable naturel avec une coloration résistante à l'eau. Cela permettrait peut-être d'une part, de montrer aux L1 comment le sable sédimente réellement, et d'autre part de pallier le problème des mauvaises tailles du sable EMRiver (en effet, chaque particule colorée ne fait pas forcément la taille indiquée).
Pour résumer, nous allons devoir trouver du sable, voire en synthétiser, et créer un système de coloration pour illustrer notre modèle.
Séance 1 : Introduction rédigée, visite et découverte des différents substituts utilisables, ébauches d'idées pour la prochaine séance (sachant que nous devrions avoir l'opportunité d'utiliser un bac en plastique et non en bois pour limiter les fuites):
- Tout d'abord, pour bien visualiser les processus naturels, nous utiliserons du sable naturel de granulométrie variée (gravier à limon).
- Ensuite nous essaierons de reproduire le modèle avec des broyats de plastique recyclé (avantageux puisqu'ils sont déjà colorés, désavantageux puisqu'ils ne suivent pas le schéma de sédimentation classique).
Si nous finissons par utiliser du sable naturel, il faudra prendre en compte premièrement la densité des grains, mais aussi leur colorimétrie (à savoir si nous pouvons directement avoir du sable naturellement teint ou s'il faudra le colorer artificiellement).
- Utiliser différents sables naturellement colorés, que nous pourront tamiser pour trier les gros grains des petits
Séance 2 :
Afin de s’assurer de la faisabilité de nos expériences, il nous faut définir les conditions dans lesquelles elles doivent se dérouler. Nous voulons travailler dans un régime laminaire, à savoir non-turbulent, tout en assurant le transport de notre sable pour ce modèle. Pour ce faire, nous utiliserons le diagramme de Hjulstrom qui illustre l’influence de la granulométrie des particules sur leur transport et leur vitesse de sédimentation.
Nous cherchons un débit pour lequel les grains érodent et sédimentent sous un régime laminaire. Pour cela, nous avons besoin du nombre de Reynolds qui permet d’établir la nature du régime (si le nombre de Reynolds est compris entre 500 et 2000, on pourra considérer que le régime est laminaire).
Re = LV/𝛎
avec 𝝂 = la viscosité connue de l’eau douce.
Comme nous travaillons avec de l’eau douce à température ambiante (~20°C), 𝝂 = 10^-6 m²/s.
Nous trouverons la vitesse générale du fluide grâce au diagramme, et la longueur vaut 5 cm (qui correspond approximativement à la largeur attendue de notre rivière)
En supposant que nos grains de sable sont de tailles comprises entre 0,5 et 5mm, nous avons cherché sur le diagramme quelle vitesse correspondrait au transport des tailles minimale et maximale des particules.
Nous trouvons alors une vitesse de fluide minimale, pour un grain de 0,5 mm, de 3cm/s et une vitesse maximale, pour un grain de 5mm, de 20cm/s.
Sachant que la viscosité est de 10⁻6 m²/s, alors que les deux autres données sont en cm et cm/s, il faut la convertir en cm²/s. Ainsi, comme 1m²/s = 10⁴ cm²/s, alors la viscosité de l’eau douce vaut 10⁻2 = 0,1 cm²/s.
Re(min) = ((5x3)/0,1) = 150
Re(max) = ((5x20)/0,1) = 1000
Pour un grain de 5mm, nous trouvons une vitesse de fluide minimale de 20cm/s et maximale de 70cm/s. On a:
Re(min) = ((5x20)/0,1) = 1000
Re(max) = ((5x70)/0,1) = 3 500
Comme Re(min) du grain de 0,5mm vaut 150<500 et que Re(max) du grain de 5mm vaut 3500>2000, nous pouvons exclure ces deux valeurs extrêmes de nos expériences. De plus, il s’avère que la vitesse minimale permettant le transport d’un grain de 5mm est égale à la vitesse maximale permettant le transport d’un grain de 0,5mm. C’est pourquoi nous pensons que cette vitesse de 20cm/s, ayant pour nombre de Reynolds = 1000, caractéristique d’un régime laminaire, serait une vitesse adéquate pour notre expérience.
La vitesse étant définie, nous pouvons calculer le débit de la rivière modélisée. De plus,
Q = S x v
avec Q le débit, S la section de la rivière (son aire) et v la vitesse du fluide v = 20 cm/s
Supposons que la rivière obtenue fasse en moyenne 0,5 cm de haut pour 5 cm de large. Alors S = 2,5 cm².
Le débit nécessaire au transport des particules sableuses et à un système laminaire correspond donc à Q = 2,5 * 20 = 50 cm^3 /s.
Pour obtenir le débit, on utilise le montage de nos prédécesseurs afin de mesurer le flux à la sortie d'eau.
Pour la prochaine fois, on mesurera le débit expérimentalement en observant le temps nécessaire à l'obtention d'un litre d'eau. Ensuite, on divisera le volume par ce temps.
Après cela, nous pourrons chercher à modéliser avec du sable, au moins deux sables différents pour avoir une idée de la vitesse du tri (si c'est bien faisable en deux heures, sachant que l'objectif premier est de réaliser cette expérience en TP).
Séance 3 : Nous avons essayé de trouver un moyen d'adapter le système de l'an passé aux nouvelles contraintes (notamment dues au changement de bac, le précédent en bois ayant beaucoup de fuites). Nous avons essayé expérimentalement d'obtenir le débit adéquat de 50 cm^3/s. Sachant que 1cm³ = 1mL, nous cherchons donc 50 mL/s.
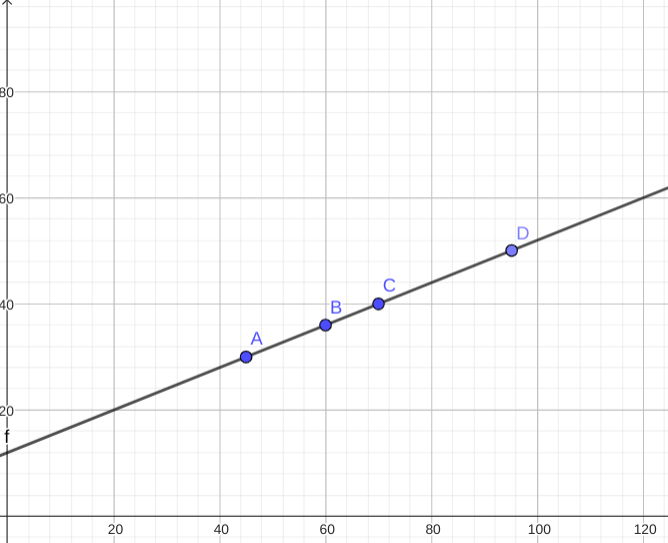
Pour ce faire, nous avons fait un test avec la pompe, rattachée à un moteur auquel nous avions arbitrairement attribué la valeur de 45, et nous avons obtenu 30mL/s, sachant que 1cm³ = 1mL, nous avons alors fait un test avec le moteur à 60. Nous avons obtenu 37 mL/s. Ensuite, nous avons monté le moteur à 70 et avons alors obtenu 40 mL/s. Les trois points obtenus semblant linéaire, nous les avons reportés graphiquement ci dessous :
Graphique du débit ( mL/s ) en fonction de la puissance du moteur de la pompe
Nous avons ainsi pu obtenir la puissance du moteur associée au débit de 50 mL/s. Nous avons trouvé le point D, pour lequel l’abscisse vaut 95. Expérimentalement, nous associons bien cette puissance a un débit de 50mL/s. Cependant, il s'est avéré que l'eau ne passait plus assez vite du contenu pour la décantation au contenu avec la pompe... Le système débordant d'eau, nous allons dorénavant baser nos recherches sur des grains de taille inférieure à 5 mm.
Prenons en compte des sables compris entre 0,5 et 2 mm. Alors, comme vu précédemment, la vitesse de fluide pour pouvoir déplacer un grain de 0,5 mm est comprise entre 1 et 20 mL/s. De plus, nous pouvons voir que celle nécessaire au transport d'un grain de 2 mm est comprise entre 10 mL/s et 50 mL/s. Pour ménager la pompe, nous pourrons prendre la vitesse minimale de transport des grains de 2 mm, qui est donc égale à 10 mL/s. Vérifions qu'avec cette vitesse, nous sommes toujours en régime laminaire : Re(10) = ((5x10)/0,1) = 500, cette vitesse convient donc.
Alors, le débit associé devra être égal à Q = S*v = 2,5*10 = 25 mL/s.
En reprenant la droite obtenue plus haut, nous pouvons lire graphiquement la puissance du moteur nécessaire pour un tel débit : environ 30.
Cependant, en testant expérimentalement, le débit est tellement faible que l'eau ne parvient pas jusqu'au bac...
Nous avons essayé de retourner le problème : l'eau circule convenablement avec une puissance du moteur de 45. Cette dernière est associée à un débit de 30 mL/s (nous l'avons confirmé via des treplicats). Alors, la vitesse est de v = Q/S = 30/2,5 = 12 cm/s. Le système est bien laminaire, comme Re(12) = ((5x12)/0,1) = 600, donc entre 500 et 2000. De plus, cette vitesse de fluide peut transporter des grains de quartz compris entre 0,5 mm et 2 mm.
Nous avons donc trouvé le débit adéquat, qui n'engendre pas de débordement et qui est assez élevé pour atteindre le bac et transporter les particules.
Avant de pouvoir passer à la modélisation du réseau fluviatile, nous devons prendre 2 sables de couleurs différentes et les classer selon leurs tailles. C'est ce que nous avons commencé à faire, mais vu le temps nécessaire au tamisage, cela nous prendra certainement une séance.
Séance 4 : Nous avons tamisé du sable marron de 0 à 2 mm pour obtenir des grains de 1 à 2 mm. Le processus prend beaucoup de temps et nous aurons besoin de davantage de séances pour avoir un tri satisfaisant.
En parallèle, nous avons cherché en ligne un type de sable naturellement coloré afin de pouvoir obtenir un contraste dans les pigments une fois le modèle mis en place. Nous ne possédons actuellement qu'un type de sable constitué de grains majoritairement marrons et blancs. En cherchant, nous avons pu trouver des candidats potentiels, notamment du gravier d'aquarium noir de 0,6 à 1,2 mm coloré naturellement. Il reste à voir s'il est possible d'en commander en grandes quantités sachant qu'on n'est pas sûres que le résultat soit correct.
Nous avons aussi utilisé de l'encre de Chine pour colorer du sable et voir si elle ne colorait pas l'eau. Comme elle doit sécher pour être insoluble, nous allons attendre la prochaine séance pour voir si nous obtenons du sable noir qui ne déteint pas. Si cela ne fonctionne pas, nous allons devoir commander du sable naturellement coloré comme le gravier d'aquarium présenté plus haut.
Séance 5 : Nous avons reçu du sable coloré naturellement que nous allons pouvoir tamiser afin de vérifier que les tailles indiquées sont correctes.
Le sable, après tamisage, fait entre 0,5 mm et 1 mm.
Aussi, nous avons versé de l'eau sur le sable coloré à l'encre de chine afin de voir si cela colore le sable et résiste à l'eau. Le sable reste coloré, néanmoins l'eau prend la couleur également. Pour voir si le sable ne se décolore pas entièrement si on le laisse de manière prolongée exposé à l'eau, nous allons laisser une portion du sable coloré dans un tube avec de l'eau que nous vérifierons la fois prochaine.
 Sable coloré à l'encre de Chine
Sable coloré à l'encre de Chine
Sables mis dans l'eau
Le sable d'aquarium noir ne colore pas l'eau, par contre quelques grains sont trop fins et restent à la surface en formant des petits nuages. Nous avons tout de même essayé de reproduire notre modèle à petite échelle, avec une bassine miniature et des quantités de sable moindres.
Nous avons mélangé notre sable noir, se situant entre 0,5 et 1 mm, avec le sable de quartz de 1 à 2 mm. Nous les avons placés dans la bassine et appliqué les instructions laissées par nos prédécesseurs : il fallait tasser les côtés et aplanir le milieu afin d'homogénéiser le flux. Nous avons tracé un petit méandre afin de diriger le cours d'eau, notre modèle étant trop petit pour parfaitement reproduire celui souhaité.
Nous avons ensuite placé la pompe à eau et mis le moteur à 45, puis nous avons laissé l'eau couler selon cette construction :
Cependant, il manquait une légère pente pour pouvoir obtenir un méandre plus facilement. Nous avons surélevé notre bassine avec une planche en bois :
Avec ce modèle miniature, nous avons réussi à obtenir un tri satisfaisant, ce qui est encourageant pour la suite. En effet, nous observons un départ des grains et un tri au sein du cours d'eau.
Il nous faut maintenant de plus grandes quantités de sable des deux types pour la prochaine fois, afin de les trier et de pouvoir tester à grande échelle pour notre modèle.
https://youtube.com/shorts/JocE2WKhqmI
Séance 6 :
Nous avons récupéré le sable naturellement coloré en noir que nous avions laissé dans l'eau pendant une semaine, et il ne se décolore pas et ne colore pas l'eau non-plus. Il semble donc être un bon candidat pour notre sable de substitution.
Nous avons effectué le même test pour du sable coloré à l'encre de Chine et au bleu de méthylène : les deux ont conservé leur couleur, mais ils colorent l'eau. Cela peut être utile au cas où nous aurions besoin de plus de couleurs.
Aussi, nous avons reçu du gravier de 1 à 2 mm ainsi que plusieurs sacs de sable d'aquarium noir que nous allons tamiser également.
Le gravier étant mouillé, et comme nous ne pouvons pas le tamiser tant qu'il est humide (nous avons essayé de le faire sous l'eau mais les grains ne passent pas correctement), nous l'avons sécher avec un pistolet à air chaud :
Suite à quoi nous avons pu trier les graviers avec les tamis de 1mm et 2mm.
Nous avons également tamisé le sable noir, mais certains grains sélectionnés, qui font pourtant plus de 0,5 mm, flottent. Nous avons essayé de retirer ces particules, et avons décidé de les observer à la loupe binoculaire afin de mieux saisir ce phénomène, ce que nous ferons la séance prochaine.
Séance 7 :
Nous avons récupéré le sable au bleu de méthylène, mais il a moisi et a coloré l'eau. Quant à l'encre de Chine, elle colore toujours l'eau.
Nous avons poursuivi notre tri grâce au tamis 2000 µm afin de récupérer le sable inférieur à 2 mm pour notre modélisation.
Nous avons également décidé de poursuivre sur un modèle réduit. Cela nous permettra de passer moins de temps à tamiser et à diminuer les coûts concernant le sable, avec lequel nous voulions remplir une bassine 90 x 60 cm d'une profondeur de 30 cm. Nous n'avons cependant pas besoin d'une maquette aussi volumineuse pour illustrer le transport des particules, et allons donc utiliser une bassine plus petite. En transposant dans notre contenant actuelle, on a pu estimer qu'un récipient idéal ferait environ les dimensions de 60 x 40 x 15 cm.
Nous avons estimé notre quantité de sable à une dizaine de kilogrammes.
Pour rappel, nos prédécesseurs avaient conduits leurs expériences avec 11kgs de sable synthétique pour une bassine de 75 x 50 x 10 cm. Donc nos prévisions semblent cohérentes et faisables.
Séance 8 :
Nous avons fait plusieurs essais dans notre bassine 90 x 60 x 30 cm, n'ayant pas d'autre alternative pour le moment. Afin d'obtenir un modèle observable et efficace, nous avons rempli la bassine sur 54 cm en laissant 42 cm de vide afin de conserver une épaisseur correcte, soit de 5 cm.
Ces essais se sont avérés fructueux. D'ailleurs, nous pouvons observer l'avancée du sable qui forme un delta ainsi qu'un transport net des particules blanches. Nous pourrions conserver cette bassine, cependant les grains noirs ayant la même couleur que la bassine, il nous est difficile de visualiser leur transport.
Voici une vidéo illustrant les résultats de cette séance : https://youtu.be/SicIo69D0q4?feature=shared
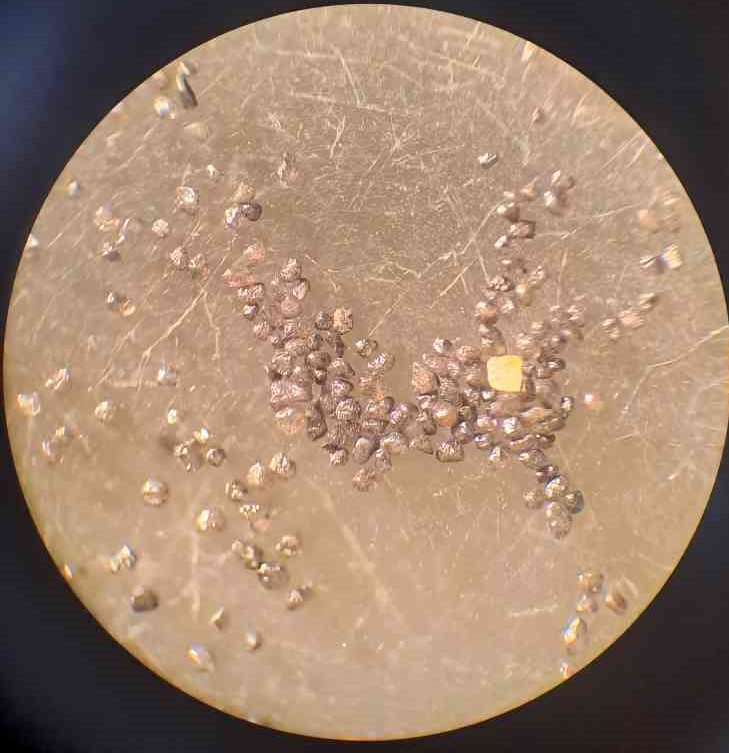
Nous avons visualisé nos grains de sable noir à la loupe binoculaire :
Séance 9 :
Nous avons contacté Madame Laurence Le Callonnec, Maître de Conférence en sédimentologie à Sorbonne Université, qui nous a reçues dans le but d'identifier notre sable noir. Après observation à la loupe binoculaire, il lui a semblé que nos grains étaient colorés artificiellement. Afin de vérifier cela, nous avons versé de l'alcool sur un premier échantillon de sable, et de l'acétone sur un second échantillon. Quelques minutes plus tard, nous les avons observés à nouveau et les grains étaient déjà partiellement décolorés. Il semblerait donc qu'il s'agisse de quartz coloré artificiellement; cependant, il ne se décolore pas naturellement et ne pose pas problème quant à notre modélisation. Néanmoins, il montre un comportement étrange vis-à-vis de l'eau : les particules les plus fines flottent et forment un léger film à la surface. Nous avions au préalable enlevé la majorité de ces grains parasites.
Nous pouvons préciser tout de même que les grains étaient vendus comme étant "naturellement colorés" sans produits chimiques ajoutés... Cependant, étant donné qu'il est aussi coûteux que le quartz non-coloré, nous considérons que nous pourrons le garder à l'avenir.
Comme notre bassine est de couleur noire, le transport de nos grains est difficilement visualisable. Nous avons donc décidé de peindre le fond de notre bassine en bleu à la bombe :
Nous allons devoir attendre que cela sèche pour refaire un essai.
Séance 10 :
Au bout d'une semaine, notre sable laissé dans l'acétone et l'alcool est entièrement décoloré. Mme Le Callonnec a identifié du quartz translucide, un peu de quartzite ainsi que quelques grains noirs opaques qui pourraient être des petits fragments de roches volcaniques.
Nous avons mis 6 litres d'eau dans les réservoirs d'eau (bac de décantation et bac d'arrivée d'eau) et avons mis le moteur à 45 comme nous le faisions auparavant. Pour faciliter le transport des grains, nous créons une pente en ajoutant une planche de 2,5 cm de hauteur, que nous disposons sous les 10 premiers centimètres de la bassine. Dans cette même optique, nous rajoutons un peu de savon dans notre eau.
Voici le résultat obtenu, filmé à l'aide d'un trépied :