EMRiver

Modèle analogique d'un système fluviatile

Lola Asensio, Jade Montagne

           Afin de rendre accessible le phénomène de sédimentation des rivières, notamment aux L1, notre but est de modéliser un cours d'eau suffisamment élaboré pour illustrer l'effet du tri des particules dans un système laminaire. Les modèles précédents nous permettent de réutiliser un mécanisme efficace pour reproduire le système aquifère. Notre priorité est de trouver un substitut au sable d'EMRiver, qui est très coûteux. Dans le meilleur des cas, nous aimerions avoir un mode de dépôt similaire à la sédimentation naturelle du sable (les grosses particules sédimentent en premier). 

           L'argument de nos prédécesseurs contre l'utilisation du sable était son manque d'esthétisme. Cependant, il semblerait qu'ils aient comparé le sable non coloré avec le sable vendu par EMRiver, et donc teinté. Nous pouvons essayer de créer du sable naturel avec une coloration résistante à l'eau. Cela permettrait d'une part, de montrer aux L1 comment le sable sédimente réellement (ils risquent de retenir le mauvais modèle, de se mélanger les pinceaux), et d'autre part de pallier le problème des mauvaises tailles du sable EMRiver (en effet, chaque particule colorée ne fait pas forcément la taille indiquée). 

Pour résumer, nous allons devoir trouver du sable, voire en synthétiser, et créer un système de coloration pour illustrer notre modèle.

Séance 1 : Introduction rédigée, visite et découverte des différents substituts utilisables, ébauches d'idées pour la prochaine séance (sachant que nous devrions avoir l'opportunité d'utiliser un bac en plastique et non en bois pour limiter les fuites):

• Tout d'abord, pour bien visualiser les processus naturels, nous utiliserons du sable naturel de granulométrie variée (gravier à limon).
• Ensuite nous essaierons de reproduire le modèle avec des broyats de plastique recyclé (avantageux puisqu'ils sont déjà colorés, désavantageux puisqu'ils ne suivent pas le schéma de sédimentation classique).

Si nous finissons par utiliser du sable naturel, il faudra prendre en compte premièrement la densité des grains, mais aussi leur colorimétrie (à savoir si nous pouvons directement avoir du sable naturellement teint ou s'il faudra le colorer artificiellement).

- Utiliser différents sables naturellement colorés, que nous pourront tamiser pour trier les gros grains des petits

Séance 2: 

           Afin de s’assurer de la faisabilité de nos expériences, il nous faut définir les conditions dans lesquelles elles doivent se dérouler. Nous voulons travailler dans un régime laminaire, à savoir non-turbulent, tout en assurant le transport et l’érosion de notre sable pour ce modèle. Pour ce faire, nous utiliserons le diagramme de Hjulstrom qui illustre l’influence de la granulométrie des particules sur leur transport et leur vitesse de sédimentation. 

DOI:10.13140/2.1.4220.4483

            Nous cherchons un débit pour lequel les grains érodent et sédimentent sous un régime laminaire. Pour cela, nous avons besoin du nombre de Reynolds qui permet d’établir la nature du régime (si le nombre de Reynolds est compris entre 500 et 2000, on pourra considérer que le régime est laminaire). 

Re = LV/𝛎
avec 𝝂 = la viscosité connue de l’eau douce.

Comme nous travaillons avec de l’eau douce à température ambiante (~20°C), 𝝂 = 10^-6 m²/s. 
Nous trouverons la vitesse générale du fluide grâce au diagramme, et la longueur vaut 5 cm (qui correspond approximativement à la largeur attendue de notre rivière)
En supposant que nos grains de sable sont de tailles comprises entre 0,5 et 5mm, nous avons cherché sur le diagramme quelle vitesse correspondrait au transport des tailles minimale et maximale des particules.
Nous trouvons alors une vitesse de fluide minimale, pour un grain de 0,5 mm, de 3cm/s et une vitesse maximale, pour un grain de 5mm, de 20cm/s.
Sachant que la viscosité est de 10⁻6 m²/s, alors que les deux autres données sont en cm et cm/s, il faut la convertir en cm²/s. Ainsi, comme 1m²/s = 10⁴ cm²/s, alors la viscosité de l’eau douce vaut 10⁻2 = 0,1 cm²/s.

Re(min) = ((5x3)/0,1) = 150

Re(max) = ((5x20)/0,1) = 1000

Pour un grain de 5mm, nous trouvons une vitesse de fluide minimale de 20cm/s et maximale de 70cm/s. On a:

Re(min) = ((5x20)/0,1) = 1000

Re(max) = ((5x70)/0,1) = 3 500

Comme Re(min) du grain de 0,5mm vaut 150<500 et que Re(max) du grain de 5mm vaut 3500>2000, nous pouvons exclure ces deux valeurs extrêmes de nos expériences. De plus, il s’avère que la vitesse de minimale permettant le transport d’un grain de 5mm est égale à la vitesse maximale permettant le transport d’un grain de 0,5mm. C’est pourquoi nous pensons que cette vitesse de 20cm/s, ayant pour nombre de Reynolds = 1000, caractéristique d’un régime laminaire, serait une vitesse adéquate pour notre expérience.
La vitesse étant définie, nous pouvons calculer le débit de la rivière modélisée. De plus,

Q = S x v

avec Q le débit, S la section de la rivière (son aire) et v la vitesse du fluide v = 20 cm/s
Supposons que la rivière obtenue fasse en moyenne 0,5 cm de haut pour 5 cm de large. Alors S = 2,5 cm².

Le débit nécessaire au transport des particules sableuses et à un système laminaire correspond  donc à Q = 2,5 * 20 = 50 cm^3 /s.

Pour obtenir le débit, on utilise le montage de nos prédécesseurs afin de mesurer le flux à la sortie d'eau.

Pour la prochaine fois, on mesurera le débit expérimentalement en observant le temps nécessaire à l'obtention d'un litre d'eau. Ensuite, on divisera le volume par ce temps.
Après cela, nous pourrons chercher à modéliser avec du sable, au moins deux sables différents pour avoir une idée de la vitesse du tri (si c'est bien faisable en deux heures, sachant que l'objectif premier est de réaliser cette expérience en TP).

Séance 3 : Nous avons essayé de trouver un moyen d'adapter le système de l'an passé aux nouvelles contraintes (notamment dues au changement de bac, le précédent en bois ayant beaucoup de fuites). Nous avons essayé expérimentalement d'obtenir le débit adéquat de 50 cm^3/s. Sachant que 1cm³ = 1mL, nous cherchons donc 50 mL/s.

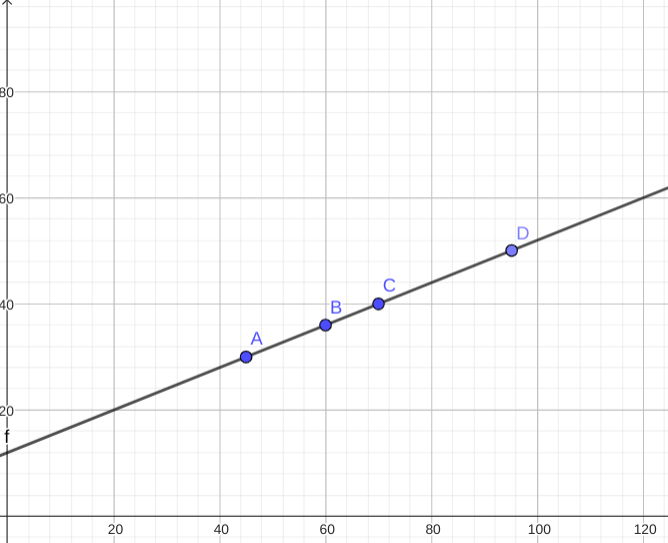
             Pour ce faire, nous avons fait un test avec la pompe, rattachée à un moteur qui était à une valeur de 45, et nous avons obtenu 30mL/s, sachant que 1cm³ = 1mL, nous avons alors fait un test avec le moteur à 60. Nous avons obtenu 37 mL/s. Ensuite, nous avons monté le moteur à 70 et avons alors obtenu 40 mL/s. Les trois points obtenus semblant linéaire, nous les avons reportés graphiquement ci dessous :

Graphique du débit ( mL/s ) en fonction de la puissance du moteur de la pompe 

Nous avons ainsi pu obtenir la puissance du moteur associée au débit de 50 mL/s. Nous avons trouvé le point D, pour lequel l’abscisse vaut 95. Expérimentalement, nous associons bien cette puissance a un débit de 50mL/s. Cependant, il s'est avéré que l'eau ne passait plus assez vite du contenu pour la décantation au contenu avec la pompe... Le système débordant d'eau, nous allons dorénavant baser nos recherches sur des grains de taille inférieure à 5 mm. 

Prenons en compte des sables compris entre 0,5 et 2 mm. Alors, comme vu précédemment, la vitesse de fluide pour pouvoir déplacer un grain de 0,5 mm est comprise entre 1 et 20 mL/s. De plus, nous pouvons voir que celle nécessaire au transport d'un grain de 2 mm est comprise entre 10 mL/s et 50 mL/s. Pour ménager la pompe, nous pourrons prendre la vitesse minimale de transport des grains de 2 mm, qui est donc égale à 10 mL/s. Vérifions qu'avec cette vitesse, nous sommes toujours en régime laminaire : Re(10) = ((5x10)/0,1) = 500, cette vitesse convient donc.

Alors, le débit associé devra être égal à Q = S*v = 2,5*10 = 25 mL/s.

En reprenant la droite obtenue plus haut, nous pouvons lire graphiquement la puissance du moteur nécessaire pour un tel débit : environ 30.

Cependant, en testant expérimentalement, le débit est tellement faible que l'eau ne parvient pas jusqu'au bac... 

Nous avons essayé de retourner le problème : l'eau circule convenablement avec une puissance du moteur de 45. Cette dernière est associée à un débit de 30 mL/s (nous l'avons confirmé via des treplicats). Alors, la vitesse est de v = Q/S = 30/2,5 = 12 cm/s. Le système est bien laminaire, comme Re(12) = ((5x12)/0,1) = 600, donc entre 500 et 2000. De plus, cette vitesse de fluide peut transporter des grains de quartz compris entre 0,5 mm et 2 mm.

Nous avons donc trouvé le débit adéquat, qui n'engendre pas de débordement et qui est assez élevé pour atteindre le bac et transporter les particules.

Avant de pouvoir passer à la modélisation du réseau fluviatile, nous devons prendre 2 sables de couleurs différentes et les classer selon leurs tailles. C'est ce que nous avons commencé à faire, mais vu le temps nécessaire au tamisage, cela nous prendra certainement une séance.

 

Séance 4: Nous avons tamisé du sable marron de 0 à 2 mm pour obtenir des grains de 1 à 2 mm. Le processus prend beaucoup de temps et nous aurons besoin de davantage de séances pour avoir un tri satisfaisant. 

En parallèle, nous avons cherché en ligne un type de sable naturellement coloré afin de pouvoir obtenir un contraste dans les pigments une fois le modèle mis en place. Nous ne possédons actuellement qu'un type de sable constitué de grains majoritairement marrons et blancs. En cherchant, nous avons pu trouver des candidats potentiels, notamment du gravier d'aquarium noir de 0,6 à 1,2 mm coloré naturellement. Il reste à voir s'il est possible d'en commander en grandes quantités sachant qu'on n'est pas sûres que le résultat soit correct.

Nous avons aussi utilisé de l'encre de Chine pour colorer du sable et voir si elle ne colorait pas l'eau. Comme elle doit sécher pour être insoluble, nous allons attendre la prochaine séance pour voir si nous obtenons du sable noir qui ne déteint pas. Si cela ne fonctionne pas, nous allons devoir commander du sable naturellement coloré comme le gravier d'aquarium présenté plus haut.