Groupe B1
Nom des participants :
- MABIRE
LéLéna - OLAGNIER Nans
- PENOT
LéLéonard - TROUDE Thibault
SéSéance 1 : PréPrésentation de l'UE et du FABLAB
 (Espace de
(Espace de dédétente àà l'entréentrée du Fablab)
Nous avons commencécommencé cette premièpremière séséance de l'UE LU1SXPFL, qu'on appelle plutôplutôt "Projet Fablab" en dédécouvrant le principe du Fablab, que l'on peut rérésumer en un bac àà sable scientifique accessible àà tout niveau, et que l'on peut utiliser en respectant le principe d'ouverture et de partage. Dans l'Openspace du Fablab, on a accèaccès àà diverses machines (imprimante 3D, fraiseuse numénumérique, dédécoupeuse laser, etc...) afin de faire, comme le disait Neil Gershenfeld, le professeur au M.I.T. crécréateur du concept des Fablabs : "anything [we want]", soit "tout [ce qu'on veut]".
Le plus important àà retenir est que dans cette UE, et dans notre utilisation du Fablab en génégénéral, mêmême pour un usage personnel, il faut entretenir ce wiki, et accompagner nos projets d'une documentation la plus préprécise possible afin que chacun, mêmême dans le futur, puisse utiliser ce que nous avons fait, comme nous utilisons ce que d'autres ont fait dans le passépassé.
 (Imprimantes 3D du FabLab)
(Imprimantes 3D du FabLab)
SéSéance 2 : DéDécouverte des logiciels de dessin
Lors de la deuxièdeuxième séséance du Projet Fablab, nous avons appris àà utiliser 3 logiciels de dessin numénumérique : Inkscape pour le dessin 2D, ainsi que OpenSCAD et FreeCAD pour le dessin 3D. A la fin de la séséance, on nous as montrémontré comment utiliser les diffédifférentes machines que nous aurons àà notre disposition lorsque nous mettrons en oeuvre notre projet : imprimante 3D et dédécoupeuse laser.
CommençCommençons par dédécrire un peu les logiciels : Inkscape est un logiciel de modémodélisation numénumérique en 2 dimensions. Pour faire simple, c'est de la géomégéométrie dans un plan en 2 dimensions. L'utiliser nous permettra de faire les plans àà mettre dans la dédécoupeuse laser. 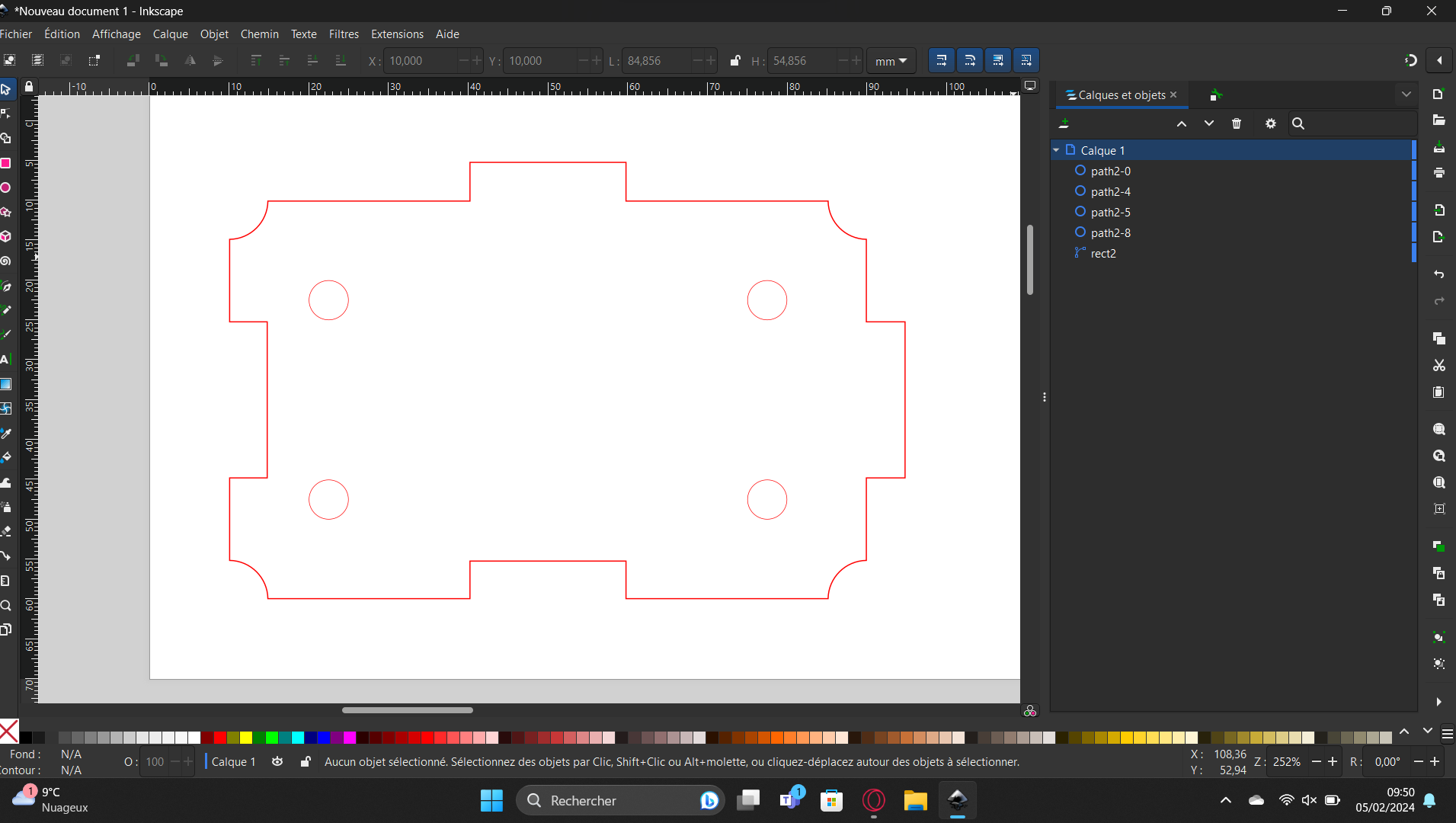

Voici ci-dessus le dessin que nous avons réaliséréalisé pendant le cours. Notre professeur nous avait demandédemandé de faire seulement un rectangle avec des cercles àà l'intéintérieur, mais nous avons voulu nous amuser en creusant les coins et en ajoutant des rectangles sur les côtécôtés pour agrandir ou rétrérétrécir la pièpièce, comme un puzzle.
Ensuite, nous avons appris àà utiliser le logiciel OpenSCAD. C'est un logiciel de modémodélisation en 3 dimensions, cette fois, et qui est basébasé sur du codage. Ainsi, on peut avec ce logiciel crécréer des formes plus ou moins complexes dans les 3 dimensions d'un plan, avec simplement quelques lignes de code (cela peut sembler compliquécompliqué, mais çça ne l'est pas tant que çça en véritévérité, les lignes de code sont simples àà comprendre et àà utiliser).
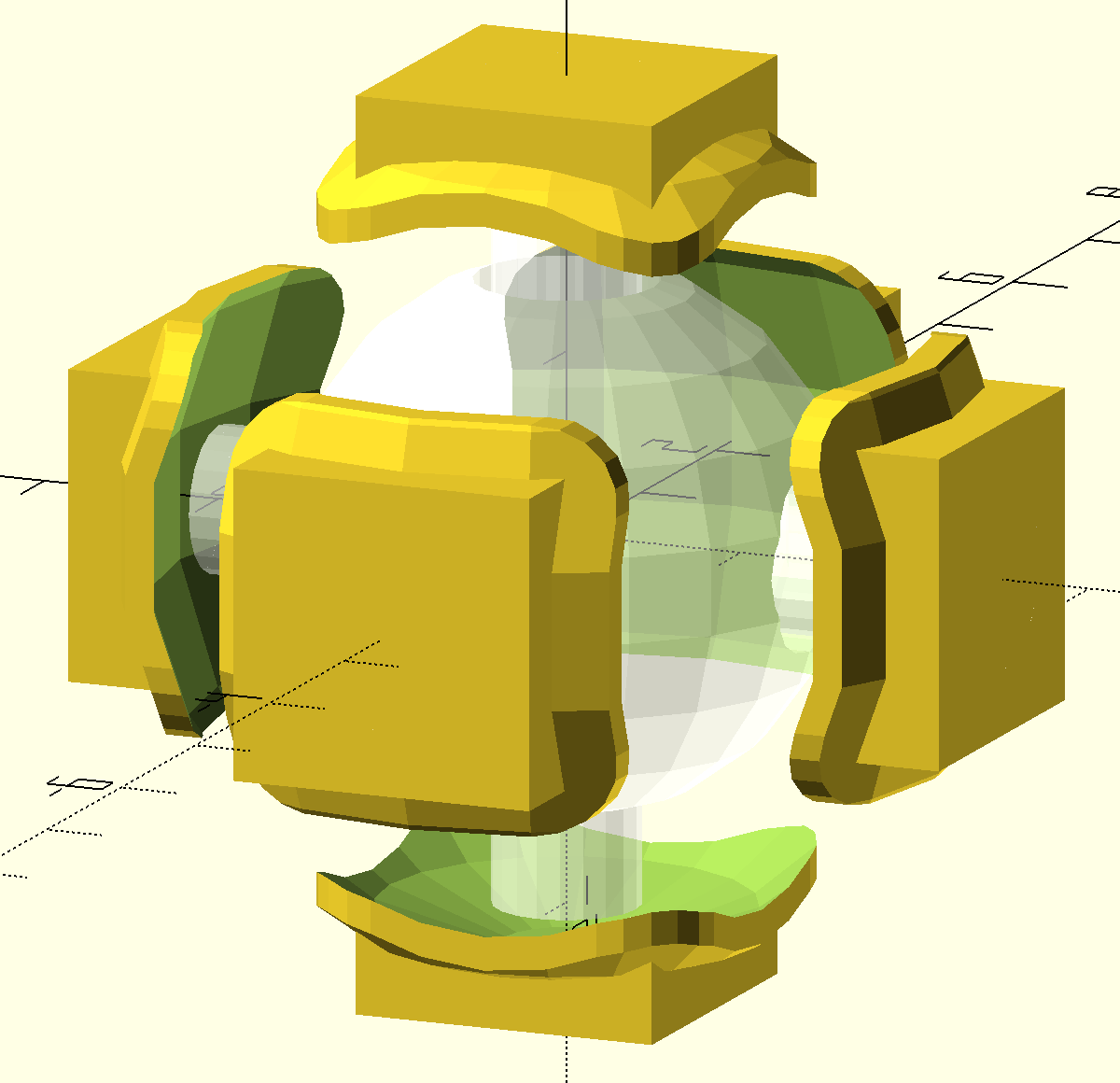
Voici pour illustrer une crécréation que nous avons fait ainsi que le code qui nous as permis de la produire. Normalement, en copiant exactement le mêmême code sur OpenSCAD, vous devriez obtenir le mêmême rérésultat (àà la seule diffédifférence que l'image de gauche est tirétirée de la visionneuse 3d de Windows 11 avec le fichier STL créécréé avec ce code, car le rendu est plus joli que celui directement disponible sur le logiciel OpenSCAD). Notre professeur nous demandait uniquement de trouer un carrécarré, mais nous avons aussi voulu aller plus loin, en crécréant des carrécarrés et des sphèsphères, et en les emboîemboîtant les uns dans les autres
$fn=300;
module coque(){
difference(){
sphere(d=30);
translate([0,0,-16])cylinder(h=40,r=9);
rotate([0,90,0])translate([0,0,-16])cylinder(h=40,r=9);
rotate([90,0,0])translate([0,0,-20])cylinder(h=40,r=9);
};
};
difference(){
coque();
sphere(d=28);
};
module tesseract(){
rotate([45,45,45])difference(){
cube(12,center=true);
translate([0,0,-8])cylinder(h=30,r=5);
translate([-12,0,0])rotate([0,90,0])cylinder(h=30,r=5);
translate([0,12,0])rotate([90,0,0])cylinder(h=30,r=5);
sphere(d=15);
};
};
tesseract();
module boule(){
rotate([-45,-45,-45])difference(){
sphere(d=9);
translate([0,0,-16])cylinder(h=40,r=2.7);
rotate([0,90,0])translate([0,0,-16])cylinder(h=40,r=2.7);
rotate([90,0,0])translate([0,0,-20])cylinder(h=40,r=2.7);
sphere(d=8);
};
};
boule();
cube(3,center=true);
sphere(d=3.5); En soit ici, le code est globalement le mêmême pour chaque partie de la figure, si ce n'est que nous n'utilisons pas les mêmêmes figures géomégéométriques àà chaque fois.
Le troisiètroisième logiciel que nous avons appris àà utiliser est FreeCAD qui est aussi un logiciel de modémodélisation 3D. C'est aussi un logiciel dit paraméparamétrique comme OpenSCAD àà la diffédifférence que FreeCAD n'est pas basébasé sur le codage mais sur l'utilisation de fonction comme la crécréation de bloc, l'extrusion et autres. Bien que cela paraisse plus simple que OpenSCAD, le logiciel FreeCAD est moins intuitif et donc plus difficile àà prendre en main.
(ModèModèle fait avec FreeCAD)
Enfin, nous avons terminéterminé la séséance en dédécouvrant un peu le fonctionnement des machines. Nous ne dédétaillerons pas ici la façfaçon exacte d'utiliser l'imprimante 3D et la dédécoupeuse laser. Tout ce que nous dirons, c'est que ces machines sont assez impressionnantes (notamment la dédécoupeuse laser, qui nous as laissélaissés bouche bébée par sa rapiditérapidité et sa préprécision).
SéSéance 3 : DéDécouverte de l'Arduino
Lors de la troisiètroisième séséance, nous avons appris les bases de codage d'une carte Arduino et des diffédifférents capteurs qui peuvent lui êêtre attachéattachée.
Tout d'abord, on nous a distribuédistribué du matématériel : une carte Arduino, des câcâbles, une LED, des rérésistances... tout ce qu'on utilise comme matématériel en temps normal en cours d'éélectronique (mis-àà-part l'Arduino qui est nouveau pour nous). L'Arduino, c'est un systèsystème reposant sur deux choses : un logiciel pilotable depuis l'ordinateur (gratuit) et une carte que l'on peut brancher directement àà l'ordinateur. Le mémélange de ces deux choses, et quelques connaissances de base en éélectronique, nous permettent de faire ce qu'on appelle de "l'éélectronique embarquéembarqué", c'est-àà-dire de l'éélectronique, mais qu'on peut facilement faire àà la maison, sans avoir besoin de tout le matématériel des TP d'éélectro qu'on fait sur le campus de la fac.
Alors imméimmédiatement, on a appris àà faire utiliser l'Arduino. On a commencécommencé par faire le circuit "Blink". C'est l'ééquivalent en Arduino du "Hello World" dans les autres langages de programmation. Le but est trètrès simple : faire clignoter une LED.
AprèAprès avoir fait ce code, on a continuécontinué sur un circuit un peu plus utile : en branchant un capteur d'humiditéhumidité et de tempétempérature sur notre Arduino, on a pu contrôcontrôler àà chaque seconde l'humiditéhumidité et la tempétempérature autour du capteur.
SéSéance 4 : DéDébut du projet en groupe
Dans cette séséance nous avons commencécommencé àà prépréparer notre projet en groupe. Notre idéidée a étéété de faire un gravimègravimètre (et dédétecteur de planèplanètes). L'objectif est donc, àà la fin de notre projet, d'obtenir un capteur capable de nous donner l'accéléaccélération de la pesanteur, et donc de nous indiquer sur quelle planèplanète on se trouve.
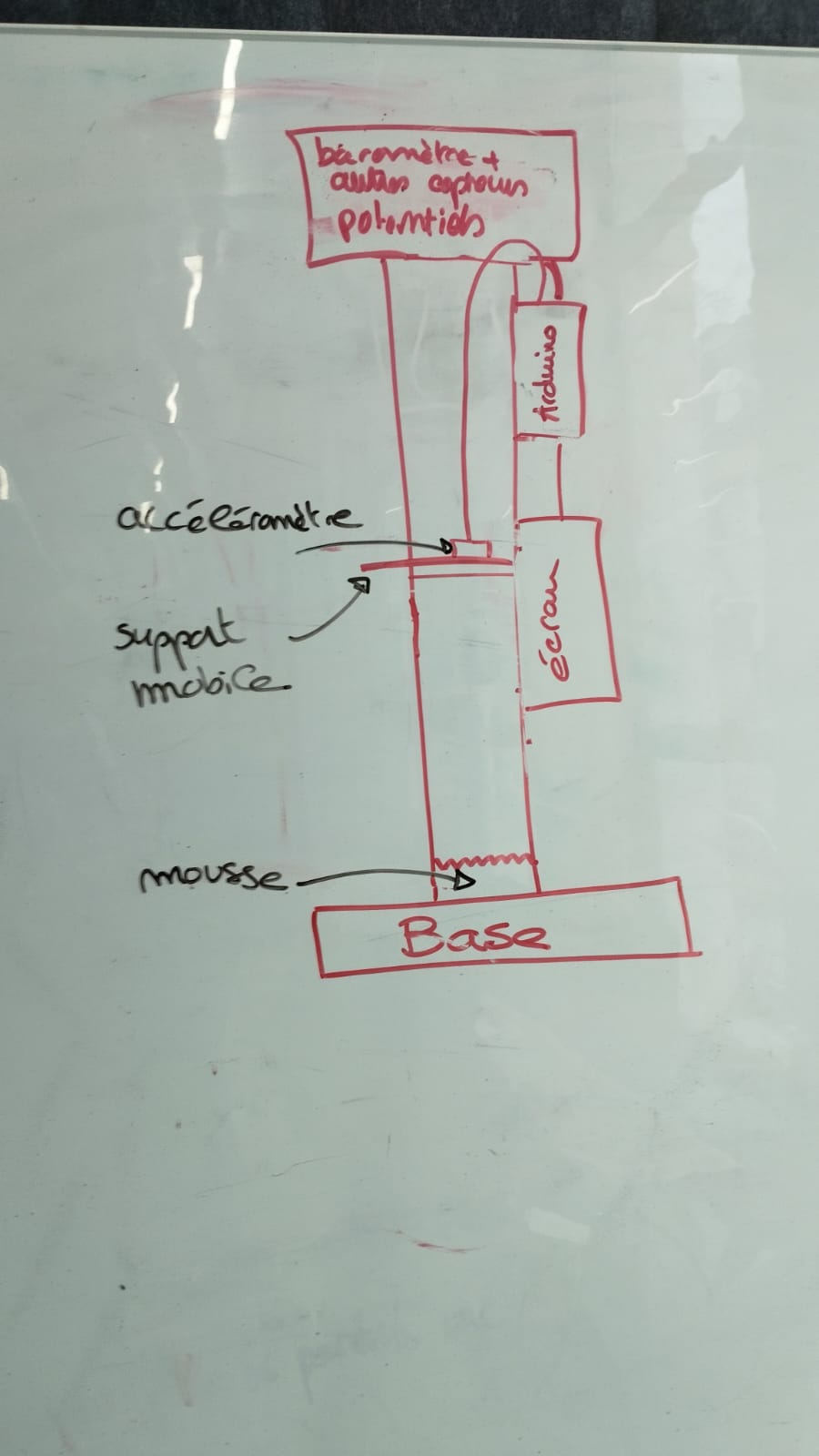
Voici un premier schéschéma de notre idéidée (sans beaucoup de dédéveloppement :
L'idéidée est la suivante : on fait tomber un accéléromèaccéléromètre, et avec une éétude mémécanique, on réréussit àà trouver l'accéléaccélération de la pesanteur (l'idéidée serait de supprimer l'incidence des frottements et de la poussépoussée d'ArchimèArchimède). Pour cela, on a eu l'idéidée de fixer l'accéléromèaccéléromètre sur un support mobile, que l'on pourrait facilement faire tomber àà l'intéintérieur d'un tube (que l'on pourrait crécréer nous-mêmême avec l'imprimante 3D et la dédécoupeuse laser). Avec un baromèbaromètre (placéplacé en haut), on pourrait connaîconnaître la pression pour calculer la poussépoussée d'ArchimèArchimède. Ensuite, en reliant le tout àà une carte Arduino, on pourrait envoyer les donnédonnées sur un éécran, et afficher ainsi la valeur de g (l'accéléaccélération de la pesanteur). En mettant dans une base de donnédonnée les valeurs tabulétabulées des accéléaccélérations de pesanteur des diffédifférentes planèplanètes du systèsystème solaire, par comparaison, notre systèsystème pourrait nous dire sur quelle planèplanète on se trouve.
Cependant, en fin de séséance, on s'est rendu compte que l'accéléromèaccéléromètre qu'on souhaitait utiliser nous donnait déjàdéjà, sans aucun mouvement, l'accéléaccélération de la pesanteur. Notre projet, dans sa conception, ne sert donc àà rien et il faut le changer. Une de nos idéidées est de partir sur un capteur de distance et de mouvement.
SéSéance 5 : GravimèGravimètre, ééquations et impression
Notre premièpremière idéidée n'ayant pas abouti, nous avons commencécommencé cette séséance en réfléréfléchissant àà comment faire notre gravimègravimètre, mais sans accéléromèaccéléromètre. AprèAprès avoir réfléréfléchi àà un capteur de distance, nous sommes finalement partis sur une idéidée de capteur de préprésence. Voici l'idéidée : dans un tube d'une soixantaine de centimècentimètres, on place trois capteurs de préprésence : deux tout en bas du tube, trètrès proches l'un de l'autre, et un tout en haut du tube. Une fois cela fait, grâgrâce àà un ressort nous envoyons une petite boule de mémétal par le bas du tube monter jusqu'au 3e capteur, puis redescendre.
Les deux premiers capteurs nous permettent de calculer la vitesse initiale de la boule, le 3e capteur nous permet, grâgrâce au temps que la boule a mis pour atteindre le haut, de connaîconnaître l'accéléaccélération de la pesanteur (on nénéglige toute autre force, comme la poussépoussée d'ArchimèArchimède et les frottements pour le moment parce qu'ils sont compliquécompliqués àà calculer et surtout assez nénégligeables ; on les rajoutera dans nos calculs àà la fin du projet si nous avons le temps).
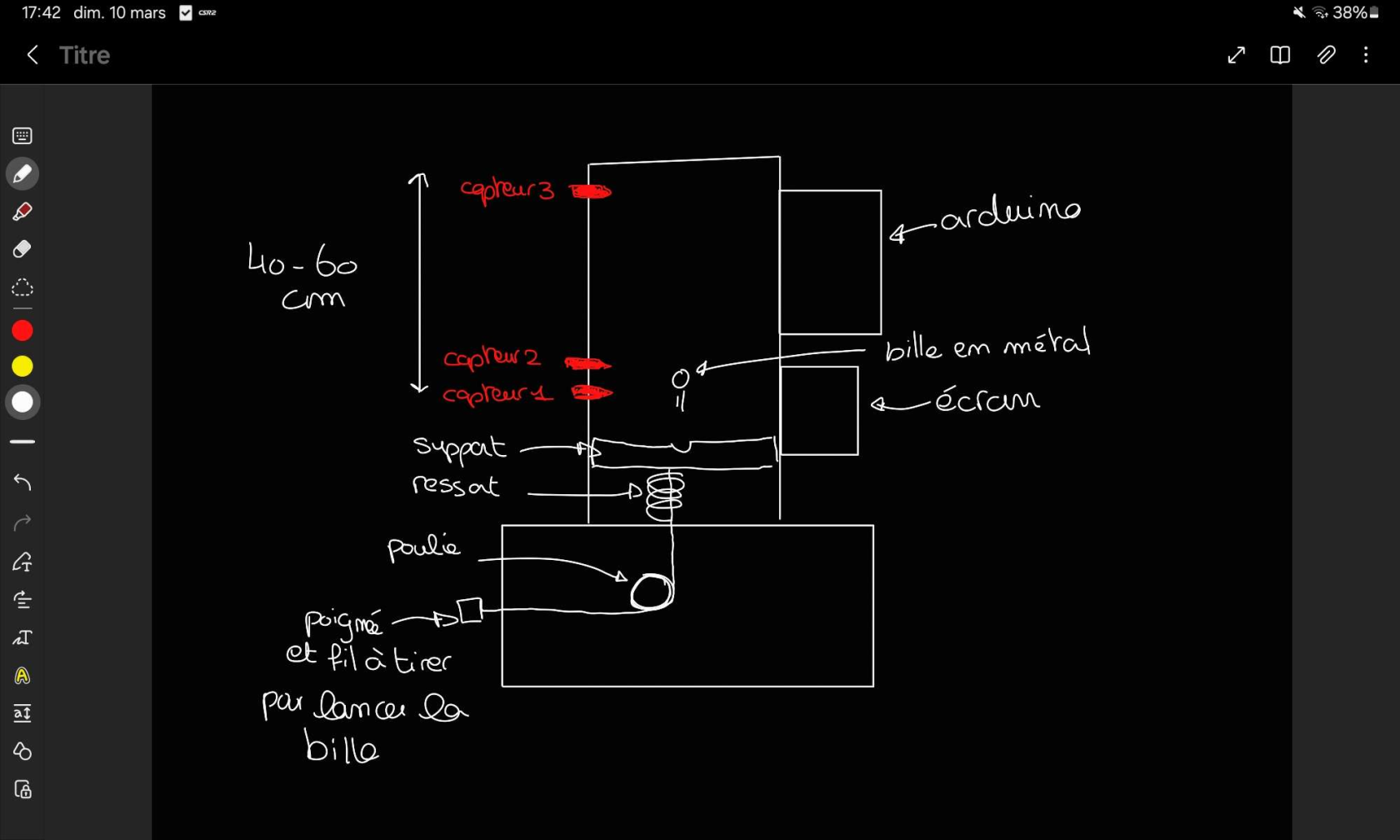
Voici ci-dessous un schéschéma de travail de notre systèsystème. C'est LéLéonard et Nans qui ont fait ce schéschéma, et Thibault et LéLéna qui ont par la suite aidéaidé àà le fignoler en fonctions des diffédifférentes valeurs que l'on devait avoir avec les capteurs :
Et ci-dessous, une photo du tableau sur lequel nous avons réfléréfléchi aux calculs que l'on devrait faire avec les capteurs :
La valeur αα est la hauteur, tandis que t est le temps. Pour les valeurs, αα1 correspond àà la hauteur du premier capteur, αα2 àà celle du 2e et αα3 àà celle du 3e tandis que les temps t1, t2 et t3 correspondent aux instants oùoù la bille en mémétal passe devant les capteurs 1, 2 et 3.
GrâGrâce aux capteurs 1 et 2, on calcule avec le ThéorèThéorème des Accroissements Finis la valeur v0, la de la boule lorsqu'elle est au premier capteur (en véritévérité, ce n'est pas exactement çça, mais on placera les capteurs suffisamment proche pour qu'on puisse l'approximer). Ensuite, en connaissant le temps t3 oùoù la boule arrive au 3e capteur, on finit par trouver la dernièdernière formule pour trouver g, l'accéléaccélération de la pesanteur. On a retrouvéretrouvé cela en faisant une analyse mémécanique et cinécinématique de la situation, en considéconsidérant que la boule n'est soumise qu'àà son propre poids.
ÀÀ la fin de la séséance, LéLéna et Thibault avaient réréussi àà faire fonctionner les capteurs tandis que Nans et LéLéonard ont impriméimprimé une premièpremière pièpièce de la machine finale, àà savoir le support de la boule, qui accrochéaccroché au ressort, permettra d'envoyer la boule faire une chute libre. Voici la pièpièce :
Sur cette photo la modémodélisation de la pièpièce sur IdeaMaker. On ne le voit pas bien, mais c'est un cylindre avec un trou en son centre pour que la boule y tombe et une surface en hauteur légèlégèrement creusécreusée, afin d'êêtre sûsûr que la boule, lorsqu'elle y reviendra, parte du milieu.
Voici le code utiliséutilisé pour modémodéliser la pièpièce (sur OpenSCAD) :
$fn=100;
module cylindre(){
difference(){
cylinder(h=1,d=3);
translate([0,0,1])resize([3,3,0.5])sphere(d=2);
translate([0,0,0.5])sphere(d=0.75);
};
};
cylindre();SéSéance 6 : Prototypage
Maintenant que toute la partie la plus théthéorique éétait au point, éétait venue l'heure du prototypage. Au dédébut de la séséance, Thibault et LéLéna ont donc commencécommencé par essayer de faire fonctionner correctement les capteurs ensemble (faire fonctionner un seul capteur n'est pas en soit d'une trètrès grande difficultédifficulté, mais en faire fonctionner trois simultanésimultanément et les uns en fonction des autres l'est plus).
Pendant ce temps, LéLéonard et Nans ont commencécommencé le prototypage "matématériel" en tentant de faire, mais sans encore de grande préprécision, la partie basse, ou "support" sur lequel on doit poser la plateforme de la boule/bille.
Codage :
unsigned T1;
unsigned T2;
unsigned vitesse ;
bool variable1 = true ;
bool variable2 = true ; //description des variables et dédépart des variables bollébolléennes en vrai
void setup() {
Serial.begin(9600);
pinMode(6,INPUT);
}
void loop() {
delay(500);
if (variable1 ==true){ // tant que la premièpremière variable est vrai
if(digitalRead(6)==LOW) { //Si un objet passe devant le premier dédétecteur
Serial.println("yes1");
T1 = millis(); // On extrait le temps auquel l'objet est passépassé devant le dédétecteur et on met la variable en fausse pour que cette partie de la boucle s'arrete
variable1 = false;
}
else {
Serial.println("No1");
}
}
if (variable2 ==true){ //
if(digitalRead(7)==LOW) { //Si un objet passe devant le second dédétecteur
Serial.println("yes2");
T2 = millis(); // On extrait le temps auquel l'objet est passépassé devant le dédétecteur et on met la variable en fausse pour que cette partie de la boucle s'arrete
variable2 = false;
}
else {
Serial.println("No2");
}
}
if (variable1 ==false and variable2 ==false ){ // Une fois que l'objet est passépassé devant les deux dédétecteurs, on calcule sa vitesse
vitesse = 1/ (T2 - T1) ;
Serial.println("vitesse =");
Serial.println (vitesse);
}
}
Code prototype calcul vitesse initial
Pour ce code le but est de dédéterminer la vitesse initiale du projectile. Pour cela, il dédécrit un fonctionnement assez simple :
- On
dédétermine le temps T1, le moment le projectile passe devant le premier capteur. - On
dédétermine ensuite le temps T2, momentoùoù le projectile passe devant ledeuxièdeuxième capteur. - Enfin on calcule la vitesse en connaissant la distance entre les deux capteurs.
On utilise pour cela des variables boolébooléennes pour ne calculer les temps T1 et T2 une seule fois et ééviter de fausser notre calcule si un capteur se rallume et ne change donc la valeur de temps stockéstocké.
PS : ce code n'est pas dédéfinitif et sera changéchangé plus tard.
SéSéance 7 : Montage final, premièpremière partie
La séséance d'aujourd'hui avait pour but d'imprimer et de dédécouper les pièpièces qui nous manquaient ainsi que de finaliser le code.
D'abord, nous avons fini d'imprimer notre systèsystème de "catapulte", c'est àà dire le systèsystème qui va lancer une bille en l'air. Pour cela, nous avons décidédécidé de reprendre presque àà 0, juste en gardant le principe. Nous avons donc créécréé un nouveau support, avec un rail de guidage pour qu'il reste bien droit tout au long de son chemin.
$fn=100;
module support(){
cylinder(h=2,r1=1,r2=1);
translate([0.8,-0.25,0])cube([0.4,0.5,1.9]);
translate([-1.2,-0.25,0])cube([0.4,0.5,1.9]);
translate([-0.25,-1.2,0])cube([0.5,0.4,1.9]);
translate([-0.25,0.8,0])cube([0.5,0.4,1.9]);
};
module support2(){
difference(){
support();
translate([0,0,2])resize([2.5,2.5,0.5])sphere(1);
translate([0,0,1.5])sphere(0.5);
resize([0.5,0.5,1])sphere(0.25);
};
translate([-0.25,-0.25,0])cube([0.25,0.5,0.1]);
};
support2();
module creuset(){
cylinder(h=2,r1=1.05,r2=1.05);
translate([0.8,-0.30,0])cube([0.45,0.6,1.5]);
translate([-1.25,-0.3,0])cube([0.45,0.6,1.5]);
translate([-0.3,-1.25,0])cube([0.6,0.45,1.5]);
translate([-0.3,0.8,0])cube([0.6,0.45,1.5]);
};
//creuset();
module corps(){
difference(){
cylinder(6,r1=1.7,r2=1.7);
for(i=[-1:1:5]){
translate([0,0,i])creuset();
};
};
};
module couloir(){
difference(){
corps();
translate([0,0,6])resize([3.5,3.5,0.5])sphere(1);
};
};
couloir(); Le fichier en .scad utiliséutilisé sur OpenSCAD est le suivant : support-couloir.scad
Il a ensuite fallu crécréer une boite suffisamment longue pour que la bille puisse monter et pour pouvoir mettre les capteurs àà une distance assez longue pour réréduire les incertitudes que nous devrons calculer une fois les premièpremières mesures faites. Pour cette boite nous nous sommes servit du code Python www.festi.info/boxes.py/ préprésent sur le wiki du fablab pour crécréer une boite de 10cm*10cm*50cm àà dédécouper àà l'imprimante laser puis àà assembler.
Pour le code, nous avons mis le calcul de l'accéléaccélération dans le code.
SéSéance 8 + vacances : Montage final, deuxièdeuxième partie
Lors de cette séséance, certain se sont concentréconcentré sur l'assemblage de la boite et des capteurs pendant que les autres terminaient le code. Pour êêtre sur que la bille retombe dans le propulseur il a fallu créécréé une pièpièce qui réréceptionne la bille et qui la ramèramène au centre. Nous avons aussi revu le code et les formules liéliée aux capteurs, pour corriger les erreurs et ajouter les parties manquantes.
$fn=100;
difference(){
translate([0,0,5]) cube([9.4,9.4,10], center = true);
translate([0,0,15.8]) sphere(10) ;
translate([0,0,-1]) cylinder(8,r1=1.7,r2=1.7);
cube(11,center=true);
}; 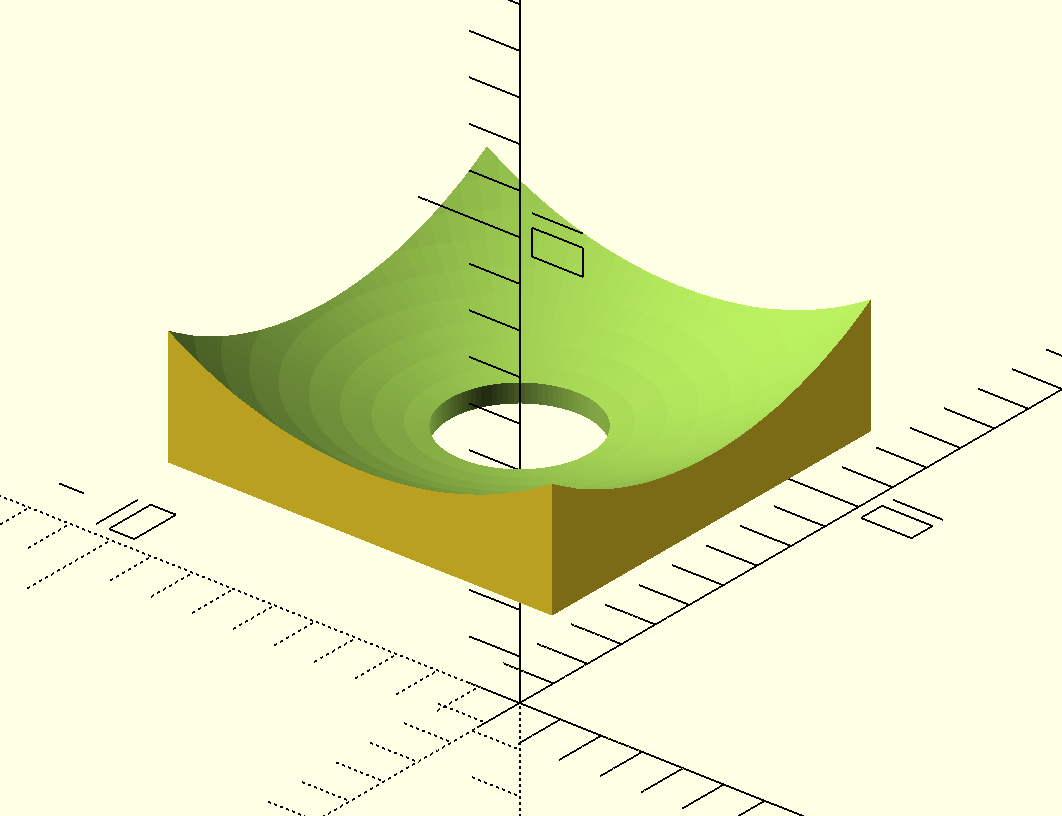


 Cette
Cette pièpièce a ensuite étéété accrochéaccrochée au propulseur.
Nous avons cependant rencontrérencontré le problèproblème que la bille ne passait pas devant tout les capteurs car ceux ci n'éétaient pas correctement alignéaligné.
Pour le code, il a fallu faire attention que l'ordre de prioritépriorité des opéopérations dans les calculs soit correcte. Nous en sommes arrivéarrivé àà ce rérésultat final :
float T1;
float T2;
float T3;
float v ;
float g;
bool variable1 = true ;
bool variable2 = true ; //description des variables et dédépart des variables bollébolléennes en vrai
bool variable3 = true ;
bool variable4 = true ;
bool variable5 = true ;
void setup() {
Serial.begin(9600);
pinMode(6,INPUT);
}
void loop() {
delay(0);
if (variable1 ==true){ // tant que la premièpremière variable est vrai
if(digitalRead(7)==LOW) { //Si un objet passe devant le premier dédétecteur
T1 = millis(); // On extrait le temps auquel l'objet est passépassé devant le dédétecteur et on met la variable en fausse pour que cette partie de la boucle s'arrete
Serial.println("T1 =");
Serial.println(T1);
variable1 = false;
}
}
if (variable2 ==true){ //
if(digitalRead(6)==LOW) { //Si un objet passe devant le second dédétecteur
T2 = millis(); // On extrait le temps auquel l'objet est passépassé devant le dédétecteur et on met la variable en fausse pour que cette partie de la boucle s'arrete
Serial.println("T2 =");
Serial.println(T2);
variable2 = false;
}
}
if (variable3 ==true) {
if(digitalRead(5)==LOW) {
T3 = millis();
Serial.println("T3 =");
Serial.println(T3);
variable3 = false;
}
}
if (variable1 ==false and variable2 ==false and variable4 ==true ){ // Une fois que l'objet est passépassé devant les deux dédétecteurs, on calcule sa vitesse
v = 0.05/ ((T2 - T1)/1000) ;
Serial.println("vitesse =");
Serial.println (v,6);
variable4 = false ;
}
if (variable1 ==false and variable2 ==false and variable3 ==false and variable5 ==true ){
g = (-2*(0.3-v*((T3-T1)/1000)))/(((T3-T1)/1000)*((T3-T1)/1000));
Serial.println("g = ");
Serial.println (g,6);
variable5 = false;
}
}AprèAprès les séséances : rérésolution des problèproblèmes
Comme les trous des capteurs n'éétaient pas alignéaligné nous avons décidédécidé de refaire la partie haute de notre gravimègravimètre. Pour cela nous avons redessiner une boite àà dédécouper àà la dédécoupeuse laser et nous y avons directement ajoutéajouté les trous pour les capteur pour que leurs dédécoupe soit nette et êêtre sûsûr qu'ils soient bien alignéalignés.


ModèModèle de la boite : BasedBox-2-2.svg
Ensuite nous avons, comme pour le prototype précéprécédent, peint les parois intéintérieur en noir puis vissévissé les capteurs pour les maintenir en place. 
Voici donc le modèmodèle final du gravimègravimètre.
Projet personnels :
En plus du projet de groupe, il nous est demandédemandé de faire deux projets personnels ; crécréer une illustration en 2D et modémodéliser un objet en 3D. Le but de ces deux projets est de nous familiariser avec les logiciel de modémodélisation préprésenter au dessus mais aussi d'apprendre àà nous servir des imprimantes 3D et de la dédécoupeuse laser préprésentes au fablab.
Projets personnels de LéLéna
Projets personnels de LéLéna
Projet 2D :
Pour mon projet 2D, j'ai choisi de graver une carte de tarot que j'ai pris sur internet et vectorisé à l'aide de InkScape. J'ai ensuite détouré l'image me laissant ainsi avec ceci :
J'ai ensuite mis le fichier sur la découpeuse laser qui a donc graver la partie noire et découpé la partie rouge. Voici le résultat :
Projet 3D :
Pour mon projet 3D, j'ai choisi de faire un petit chaudron à l'aide du logiciel OpenSCAD. Voici ci-dessous une photo de la représentation ainsi que le code :
| $fn = 200; module dif1(){; difference(){ base(); translate([0,0,4])cube(6, center = true); sphere(d = 4.5); }; }; module pied(){; cube(1, center = true); rotate([45,0,0])translate([0,0.5, -1])cube([1,1,2], center = true); }; module base(){; sphere(d = 5); translate([1, 1, -2])rotate([-20,0,-45])pied(); translate([1, -1, -2])rotate([-20,0,-135])pied(); translate([-1, 1, -2])rotate([-20,0,45])pied(); translate([-1, -1, -2])rotate([-20,0,135])pied(); } module poign(){; rotate([90,0,0])cylinder(1, 0.2, 0.2, center = true); rotate([90,0,90])translate([0.5, 0, 0.3])cylinder(0.5, 0.19, 0.19, center = true); rotate([90,0,90])translate([-0.5, 0, 0.3])cylinder(0.5, 0.19, 0.19, center = true); translate([0, 0.5, 0])sphere(d = 0.4); translate([0, -0.5, 0])sphere(d = 0.4); }; module poigne(){; translate([-2.9,0,0])poign(); rotate([0, 180, 0])translate([-2.9,0,0])poign(); }; module rond1(){; difference(){ sphere(d = 4); translate([2.1,0,0])cube(4, center = true); translate([-2.1,0,0])cube(4, center = true); }; }; module rond2(){; difference(){ sphere(d = 3); translate([2.1,0,0])cube(3.9, center = true); translate([-2.1,0,0])cube(3.9, center = true); }; }; module lune(){; difference(){ rond1(); translate([0,0.74,0])rond2(); }; }; module lunatique1(){; rond1(); translate([0, 4,0])lune(); translate([0, -4,0])rotate([0,0,180])lune(); }; module lunatique(){; resize([0.4,1.2,0.8],1)lunatique1(); }; module marmiton(){; poigne(); dif1(); translate([0,2.5,0])rotate([0,0,90])lunatique(); }; marmiton(); |
Malheureusement, la première impression a dû être arrêté au bout de 5-6 minutes car le support s'était décollé puis la deuxième impression s'est arrêté pour manque de filament mais je n'ai pas pu la reprendre car elle avait déjà été enlevé de l'imprimante me laissant avec ceci :
Projets personnels de Nans
Projets personnels de Nans
Lors de la séséance 2, notre professeur nous as donnédonnés 2 devoirs : une modémodélisation en 2 dimensions et une modémodélisation en 3 dimensions, sans plus de contraintes que celle de la taille : pour la modémodélisation 2d, une taille maximum de 30*30 cm et pour celle en 3d, une taille maximum de 15*15*15 cm.
3D : Le RER D
J'ai trètrès rapidement eu beaucoup d'idéidées pour la modémodélisation 3d (moins pour celle en 2d), et comme j'aimais bien le logiciel OpenSCAD, j'ai passépassé du temps dessus, et j'ai alors eu l'idéidée de modémodéliser un RER (en fait une rame de type Z2N qui ééquipe notamment la ligne de RER D).
Voici d'abord le rérésultat de la modémodélisation :
Il m'a fallu environ 1h30 àà 2h pour arriver àà ce rérésultat, en comptant sur l'aide de LéLéonard et de Thibault notamment, ainsi que d'autres élèélèves d'autres groupes du CMI Physique, et en ayant déjàdéjà utiliséutilisé un peu le logiciel auparavant (voir notre partie sur la séséance 2).
Dans la suite, je vais vous dédétailler un peu comment je suis arrivéarrivé àà ce rérésultat, c'est-àà-dire vous expliquer le code que j'ai utiliséutilisé.
J'ai utiliséutilisé le logiciel OpenSCAD, et voici le code utiliséutilisé :
module rame(){
cube([4.5,14,5]);
};
module cut(){
translate([-1,0,0])rotate([0,-10,-90])cube([3,6,10]);
translate([-1,0.7,0])rotate([0,20,-90])cube([3,6,10]);
};
module rame2(){
difference(){
rame();
cut();
translate([4,14,0])rotate([0,0,180])cut();
};
};
//rame2();
module porte(){
translate([-1,3,1])cube([6,1.5,3]);
translate([-1,10,1])cube([6,1.5,3]);
};
//porte();
module fenetresp(){
translate([-2,3.1,2.5])cube([8,1.3,0.9]);
translate([-2,10.1,2.5])cube([8,1.3,0.9]);
};
//fenetresp();
module fenetresr(){
for(i=[4.6:1:9]){
translate([-1,i,1.5])cube([8,0.94,3]);
};
translate([-1,1.2,2.2])cube([8,0.5,1.2]);
translate([-1,12.2,2.2])cube([8,0.5,1.2]);
};
//fenetresr();
module fenetresc(){
rotate([-10,0,0])translate([0.2,-0.5,2])cube([4.1,0.6,2]);
};
//fenetresc();
module arrondi(){
translate([-0.2,0,4.4])rotate([0,-45,0])cube([1,16,1]);
translate([4,0,5.1])rotate([0,45,0])cube([1,16,1]);
translate([-1,0,-0.2])rotate([0,45,0])cube([1,16,1]);
translate([4.6,0,-1.1])rotate([0,-45,0])cube([1,16,1]);
};
module diff1(){
difference(){
rame2();
porte();
fenetresr();
fenetresc();
translate([4.5,14,0])rotate([0,0,180])fenetresc();
arrondi();
};
};
//diff1();
module remplissage(){
difference(){
translate([0.1,2,1])cube([4.3,10,3.8]);
fenetresp();
};
translate([0.2,2,1])cube([4.1,10,3.8]);
translate([0,4.6,2.4])cube([4.5,5.1,1.2]);
translate([0.1,1.2,2.2])cube([4.3,0.5,1.2]);
translate([0.1,12.2,2.2])cube([4.3,0.5,1.2]);
};
//remplissage();
module train(){
diff1();
remplissage();
};
//train(); On voit que c'est un code assez long, mais en partie parce qu'il est aéréaéré, et aussi parce qu'il est composécomposé de plusieurs modules, c'est àà dire des genres de "fonctions" qu'on peut réréutiliser plus tard. La premièpremière chose que j'ai fait c'est modémodéliser un cube que j'ai découpédécoupé sur les côtécôtés afin d'obtenir la forme du train. Ensuite, j'ai fait une dédécoupe àà l'intéintérieur du train afin d'obtenir des trous pour les portes. Pour les fenêfenêtres, j'ai aussi fait des dédécoupes, mais en utilisant en plus la fonction "for", un boucle qui permet de faire une mêmême opéopération plusieurs fois d'affiléaffilée. Pour donner un effet fenêfenêtre, j'ai créécréé un bloc plus petit que le train àà l'intéintérieur mêmême du train pour creuser les fenêfenêtres sur une toute petite distance. Ce bloc laissait un petit "surplus" en haut, mais que j'ai décidédécidé de laisser car çça donnait l'impression d'un câcâble qui passait sur le surface du train, moins lisse et donc un peu plus "réréaliste" mêmême si ce n'est pas vraiment l'image réréelle d'un train.
Petite préprécision : il y a plusieurs lignes avec "//" devant, ce sont des commentaires qui sont en fait des "lignes de construction". Pendant la modémodélisation, j'ai plusieurs fois modélisémodélisé les modules seuls, sans le reste du train, ou jouéjoué justement avec les modules que j'affichais et ceux que je n'affichais pas pour ajuster mes valeurs.
Enfin, on a lancélancé l'impression. J'ai eu pas mal de chance, puisque cela a fonctionnéfonctionné du premier coup, et j'ai eu mon train, dèdès le lendemain. Voici une photo du rérésultat final :
On voit que globalement, l'impression a assez bien réréussi, il y avait quelques petits morceaux un peu en trop sur le haut mais qui ont facilement étéété limélimés, et il y a une trètrès légèlégère casse en bas, mais je ne suis pas sûsûr qu'elle ne vienne pas de moi. L'impression s'est faite avec une couche de protection autour du train, option qui avait étéété activéactivée pour une impression précéprécédente que que mon impression a donc récupérérécupéré. Ce n'éétait ni volontaire ni utile, mais çça a étéété fait, et mêmême on s'en est rendus compte alors que l'impression éétait déjàdéjà trop avancéavancée pour qu'on l'arrêarrête et la relance sans la coque de protection.
Voici le fichier STL utiliséutilisé pour l'impression :
2D : MaléMalénia, ÉpéÉpée de Miquella
Pour la modémodélisation en 2D, j'ai eu beaucoup moins d'idéidées. Finalement, en voyant d'autres amis modémodéliser des personnages de mangas ou simplement de fiction, j'ai décidédécidé de modémodéliser MaléMalénia, un personne du jeu Elden Ring. Pour ce faire, j'ai choisi une image sur internet. Je voulais àà la base faire le personnage de Godfrey, mais la seule image bien que j'ai trouvétrouvé, éétait trop sombre, et la vectorisation sur Inkscape n'éétait pas belle (trop de zones noires qui ne rendaient pas bien), j'ai donc finalement optéopté pour une image plus simple de la demi dédéesse MaléMalénia, un des personnages les plus embléemblématiques du jeu.
Mais je n'éétais pas totalement satisfait de l'image. Sur le site internet Dafont, j'ai donc installéinstallé la police d'éécriture Angel Wish, une police d'éécriture qui rappelle un style médiémédiéval. J'ai alors éécrit la lélégende "Malenia, Blade of Miquella" en dessous de l'image de mon personnage, ce qui est son nom et titre complet, dans le jeu. Voici une capture d'éécran du fichier Inkscape que j'ai utiliséutilisé :
La trace rouge autour est le contour que l'imprimante laser devait dédécouper pour séséparer le dessin du reste de la planche de bois.
Est venu le temps de l'impression, et s'il a fallu repasser trois fois sur le contour pour dédécouper la planche complécomplétement (elle faisait 6 mm) l'impression s'est trètrès bien passépassé, en une quinzaine de minutes au total.
Voici une photo du rérésultat :
Projets personnels de LéLéonard
Projets personnels de LéLéonard
Nous avons un total de 2 projets personels àà produire en solitaire, l'un en 2D et l'autre en 3D. Lors des ces projet, je ne produirais pas un objet réréellement utile mais plus àà usage dédécoratif.
Projet 2D :
Ce projet est réaliséréalisé avec le logiciel Inkscape puis gravégravé ou découpédécoupé avec une dédécoupeuse laser. Dans un premier temps, on utilise le logiciel Inkscape pour obtenir un fichier 2D, personnellement j'ai simplement importéimporté une image en noir et blanc. La couleur noir est utiliséutilisée pour la gravure.
Projet 3D :
Ce projet est réaliséréalisé avec le logiciel OpenScad et Ideamaker pour modémodéliser l'objet afin de finalement l'envoyer àà l'impression 3D dans le Fablab. Le projet ne comprend qu'une seule condition, la taille limitélimité àà 15*15*15 cm soit jsuqu'àà 25 cm de long en diagonale. Mon idéidée de modémodélisation est une épéépée, plus exactement un glaive qui donnerait une impression d'êêtre entouréentouré de ronces. Je n'ai pas finis le projet en une seule fois et l'ai revu àà plusieurs reprises pour finalement avoir ce rérésultat :
J'ai produit le code en solitaire mais j'ai profitéprofité de conseils vis àà vis du design de l'épéépée en elle mêmême, par exemple l'idéidée de la lune (àà l'intéintérieur de l'éétoile sur la poignépoignée) vient de Nans et delle des embouts de la garde avec une préprécision diffédifférente entre les boules qui creusent et celles creusécreusées provient de LéLéna.
Maintenant je vais dédétailler les lignes de codes qui m'ont permis de faire celàcelà. J'ai dédéfinit une premièpremière préprécision sur 15 grâgrâce àà "$fn =15;", elle est modifiémodifiée dans les modules directement lorsque j'en ai le besoin. Je ne rentrerais pas toujours dans le dédétail de la raison des tailles ou positionnement des diffédifférents objets.
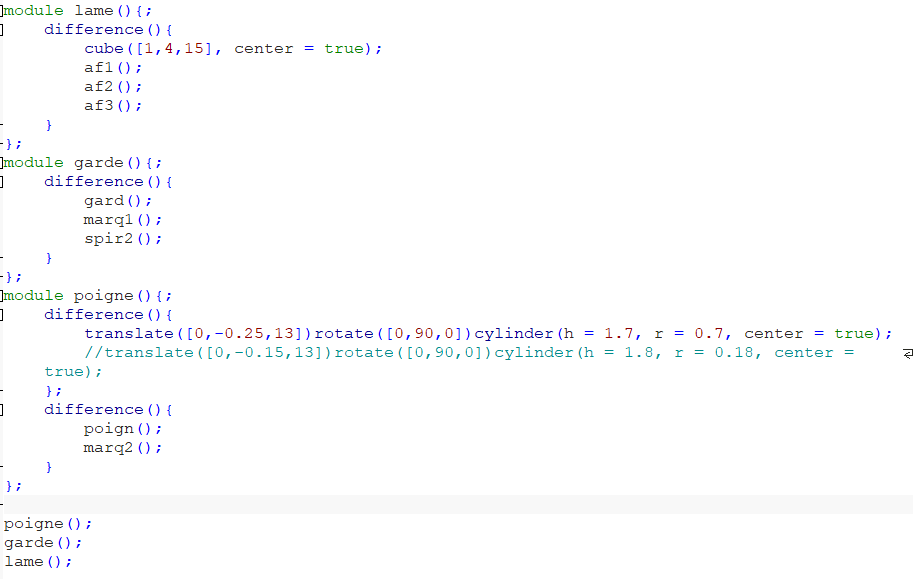
Tout d'abord mes 3 modules principaux sont les suivants :
Ils structurent les 3 parties principale du glaive et sont le rérésultat final affichéaffiché. Les 3 dernièdernières lignes permettent de les afficher. Ces modules sont tous des diffédifférences d'une forme de base simple (ensemble avec rectangle, cylindre ou boule) qui est "taillétaillée" àà l'aide d'autres modules comprenant des ensembles de formes simples. Les modules ont des noms correspondants aux zones associéassociées de l'épéépée. Lorsque l'objet "taillétaillé" est un ensemble de formes et pas uniquement un rectangle (ou autre), cet ensemble est nomménommé avec le "e" àà la fin du nom du module en moins pour avoir un code clair. Dans ce mêmême but, j'ai créécréé diffédifférent groupe de modules, comme les "af", "marq" ou "spir" pour distinguer les fonctions de ces diffédifférent modules sans s'embrouiller. La raison pour laquelle la 4è4ème ligne du module "poigne" est en commentaire est que cette ligne modémodélise un design ressemble trop àà certains signes mulsumans et bien que celàcelà soit un bel ajout, je ne souhaite pas donner une vision autre que dédécorative àà cet objet.
Ces 5 modules sont les ensembles qui vont permettre de changer la forme des modules principaux avec une diffédifférence. Le module "marq1", aurait pu êêtre simplifiésimplifié avec une fonction qui répèrépète une action et modifie àà chaque répérépétition les coordonnécoordonnées des sphèsphères mais pour pouvoir modifier plus rapidement et simplement les positions des objets, j'ai plutôplutôt optéopté pour modifier une àà une la position, dans le cas d'un ensemble plus grand (ici 10 formes passe encore) comme nous allons le voir, la méméthode sera diffédifférente.
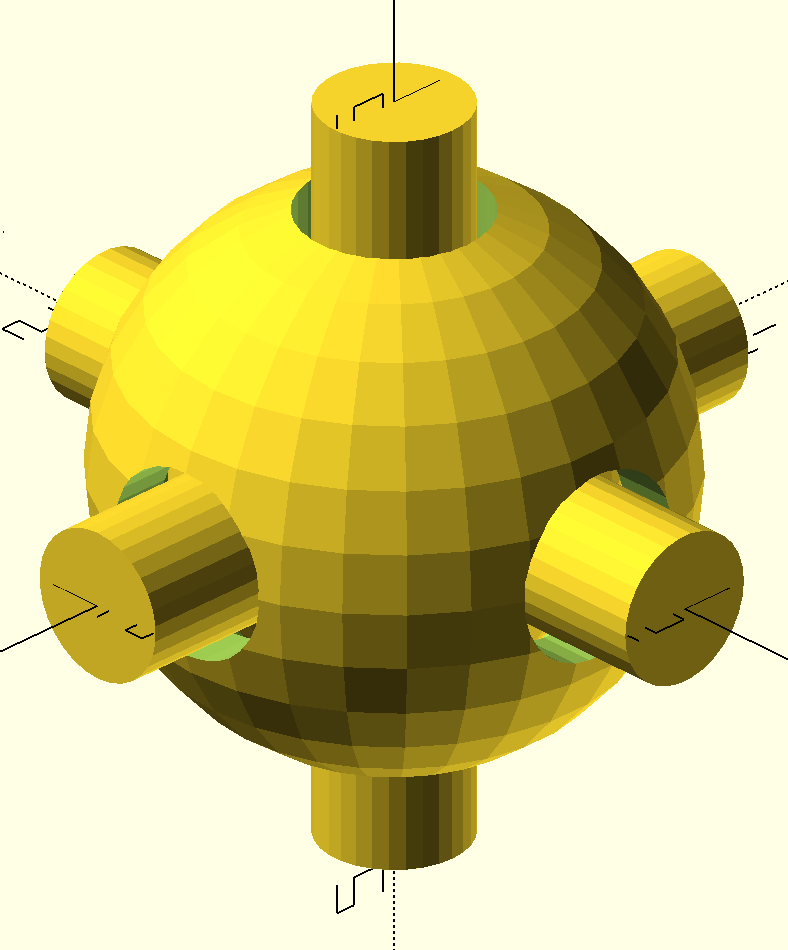
Ce groupe de module m'a permis de dédéfinir et crécréer les spirales préprésentent sur la garde et la poignépoignée. "spir2" est le module qui dédéfinit les positions des 2 spirales sur la garde et "spir1" celle sur la poignépoignée.
Le module "spir" dédéfinit la spirale de base qui est ensuite déplacédéplacée dans les autres modules. Pour ce faire, j'ai crécréer un ensemble de sphèsphères qui se succcèsucccèdent avec un dédéplacement qui eest dédéfinit par une fonction cosinus et sinus pour la rotation des sphèsphère autour de l'axe z et juste un facteur pour changer la hauteur de la sphèsphère et donner cette impression de spirale. La fonction "for" permet cette répérépétition d'action, et la variable i de modifier les valeurs des positions. Voici le rérésultat :
Enfin, il a fallu lancer l'impression 3D pour ce faire, j'ai produit un fichier que l'imprimante pouvait lire grace au logiciel ideaMaker. Ce dernier permet d'ajouter les supports pour fabriquer l'objet et de le positionner pour minimiser les surplus de matématériel.
L'impression aura pris 6 heures, en voici le rérésultat :
Projets personnels de Thibault
Projets personnels de Thibault
Pour le projet en 3D, j'ai voulu essayer de faire un systèsystème capable de bouger. J'ai donc pensépensé a faire un Rubik's cube.
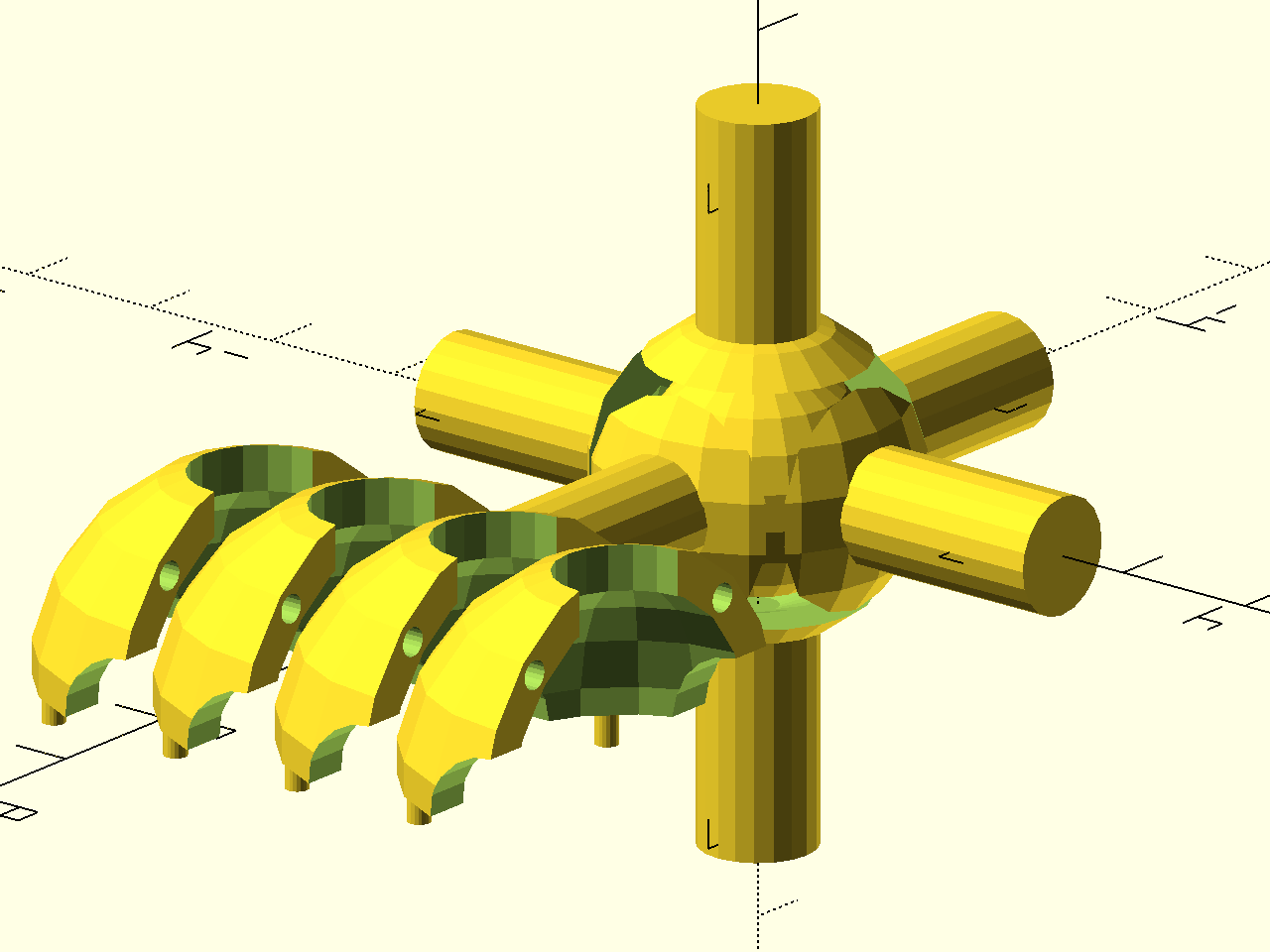
J'ai fais un premier essai mais il les pièpièces ne s'ajustaient pas donc je ne parlerai pas de cet essai. J'ai cependant pu récupérécupérer la partie centrale du Rubik's cube. Partie qui permet au pièpièce de bouger les unes par rapport aux autres.
$fn=30;
module centre(){
union(){
difference(){
sphere(1.5);
sphere(1.2);
rotate([90,0,0]) cylinder(h=15,r=0.5,center=true);
rotate([0,90,0]) cylinder(h=15,r=0.5,center=true);
rotate([0,0,90]) cylinder(h=15,r=0.5,center=true);
};
difference(){
union(){
sphere(1.1);
rotate([90,0,0]) cylinder(h=4,r=0.4,center=true);
rotate([0,90,0]) cylinder(h=4,r=0.4,center=true);
rotate([0,0,90]) cylinder(h=4,r=0.4,center=true);
};
sphere(0.9);
cube(1.6,center=true);
};
sphere(0.8);
};
};
difference(){ //permet juste de voir le fonctionnement interne, a retiréretiré lors de l'impression
centre();
cube(10);
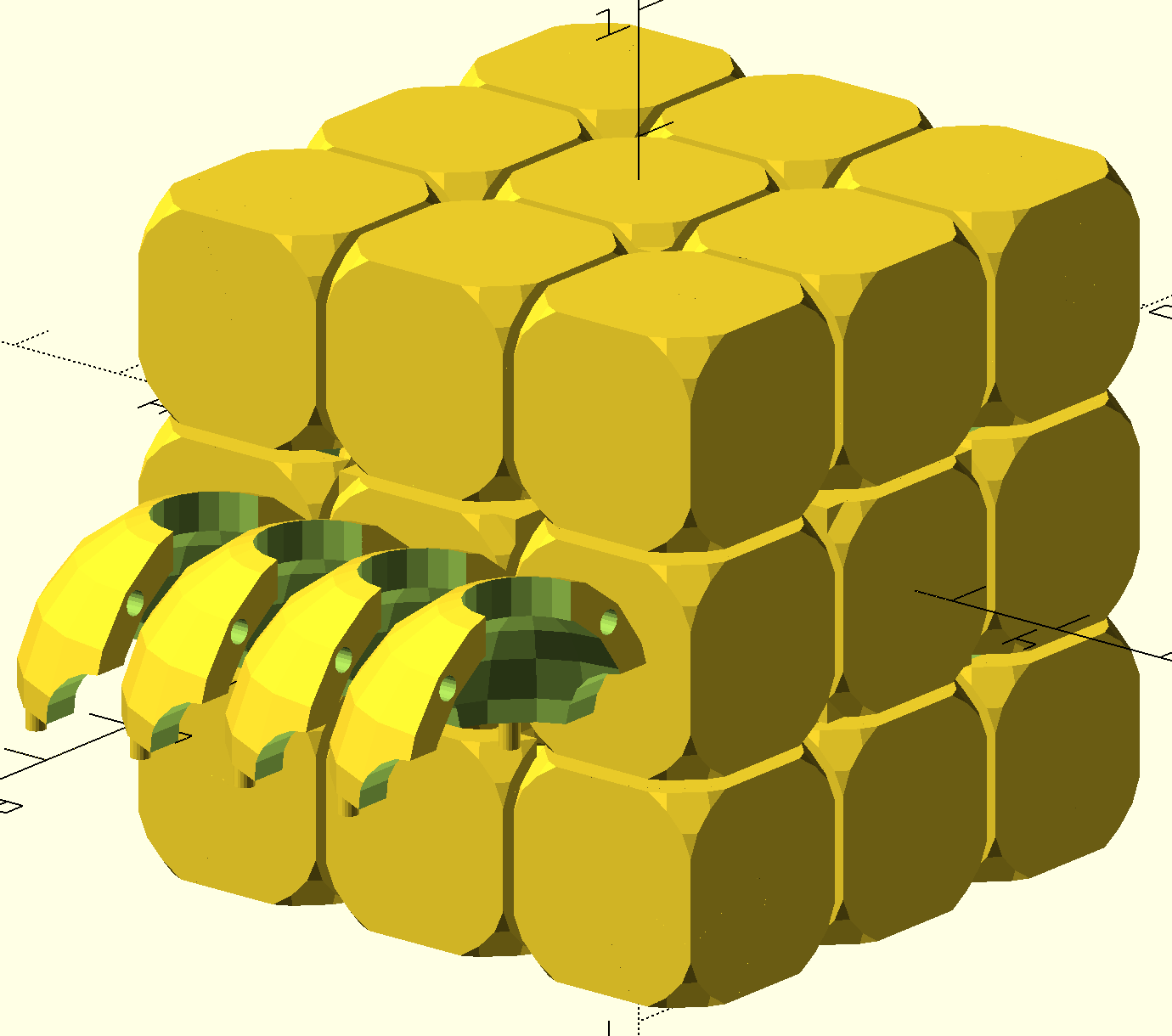
}; Lors du deuxièdeuxième essai je suis partie d'une base d'un cube forméformé d'autre petits cube grâgrâce àà une fonction for(). Cube que j'ai ensuite creusécreusé avec une sphèsphère pour pouvoir par la suite y rajouter la partie centrale montrer au dessus et les diffédifférentes formes pour que les pièpièces s'emboite.
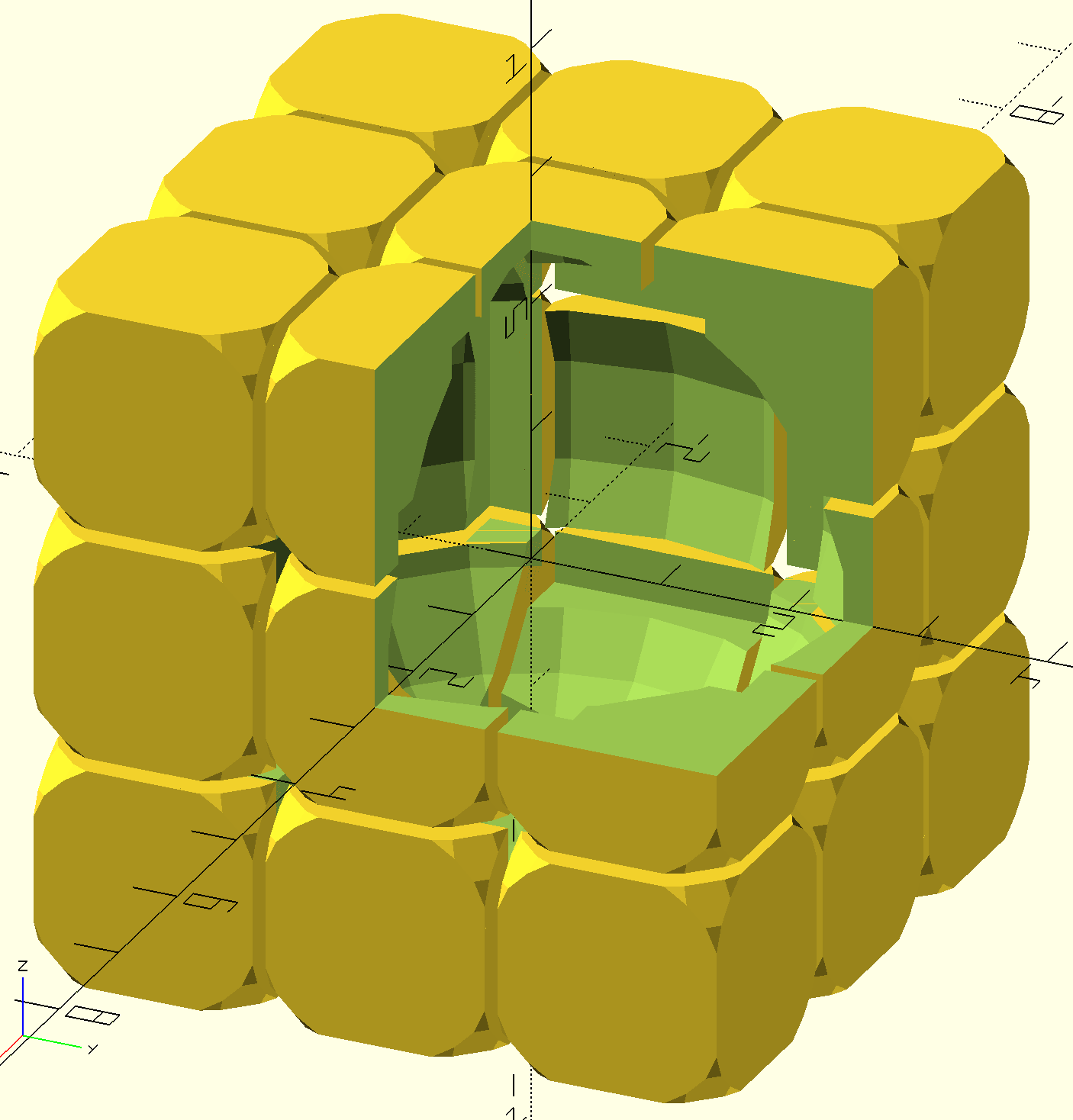
 Grand cube
Grand cube forméformés de petit cube et creusécreusé par une sphèsphère.
$fn=20;
module extrude_cote(){
difference(){
cube([1.9,4.5,2.7],center=true);
translate([0,1.8,0]) cube(1.7,center=true);
translate([0,-1.7,0]) cube(1.9,center=true);
};
};
//extrude_cote();
module cube_plein(){ //Toutes les pieces
for(i=[-1.8:1.8:1.8], j=[-1.8:1.8:1.8], k=[-1.8:1.8:1.8]) {
translate([i,j,k]) intersection(){
cube(1.7, center=true);
sphere(1.3);
};
};
};
module total(){
difference(){
cube_plein();
union(){
extrude_cote(); //creusage des pieces de cotécoté
rotate([90,0,0]) extrude_cote();
rotate([0,90,0]) extrude_cote();
rotate([0,0,90]) extrude_cote();
rotate([90,0,90]) extrude_cote();
rotate([90,90,0]) extrude_cote();
sphere(2.45); //Zone de la piece centrale
};
};
};
difference(){ //permet juste de voir l'intéintérieur
total();
cube(10);
}; Dans un Rubik's cube il y a trois type de pièpièces mobiles; les faces qui seront directement accrochéaccrochées àà la parties centrales, les coins et les cotécotés. Dans le code au dessus les pièpièces de cotécoté ont étéété creusécreusées sur les bords en plus. Cela permettra a la partie inféinférieur des faces de s'emboiter.
Pour les coins, on obtient ceci :
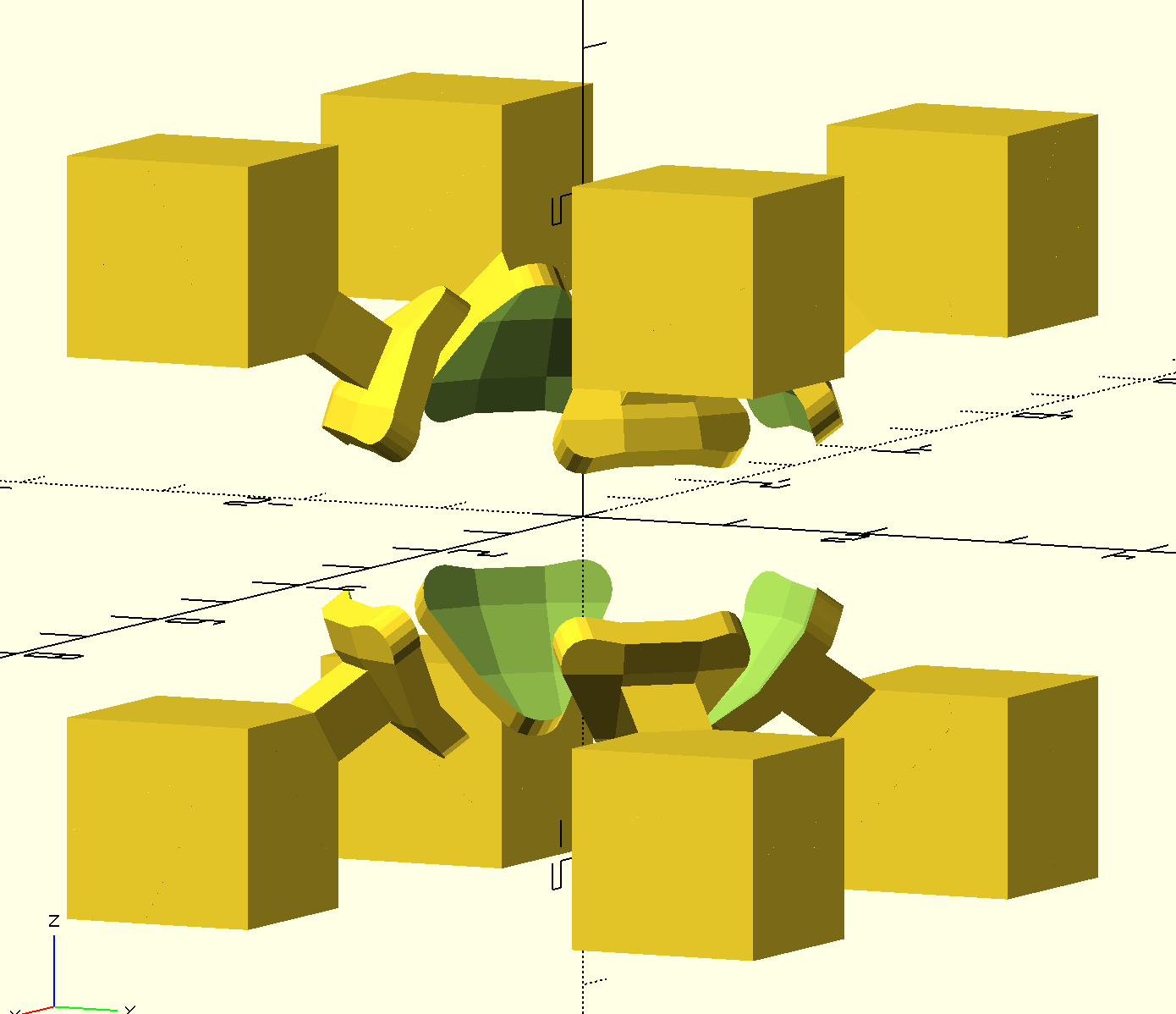

module coin(){
q=1.8;
translate([q,q,q]) cube(1.29,center=true);
translate([q,q,-q]) cube(1.29,center=true);
translate([q,-q,q]) cube(1.29,center=true);
translate([q,-q,-q]) cube(1.29,center=true);
translate([-q,q,q]) cube(1.29,center=true);
translate([-q,q,-q]) cube(1.29,center=true);
translate([-q,-q,q]) cube(1.29,center=true);
translate([-q,-q,-q]) cube(1.29,center=true);
x= 1.21/sqrt(3); y = 1.21/sqrt(3); z = 1.21/sqrt(3); // point coordinates of end of cylinder
length = norm([x,y,z]); // radial distance
b = acos(z/length); // inclination angle
c = atan2(y,x); // azimuthal angle
h=5;
r=0.2;
t=0.5;
difference(){
union(){
rotate([180, b, c]) cylinder(3, r=0.5/sqrt(3),$fn=3);
rotate([180, b, -c]) cylinder(3, r=0.5/sqrt(3),$fn=3);
rotate([0, -b+180, c]) cylinder(3, r=0.5/sqrt(3),$fn=3);
rotate([0, -b+180, -c]) cylinder(3, r=0.5/sqrt(3),$fn=3);
rotate([0, -b, -c]) cylinder(3, r=0.5/sqrt(3),$fn=3);
rotate([0, -b, c]) cylinder(3, r=0.5/sqrt(3),$fn=3);
rotate([0, -b, c+180]) cylinder(3, r=0.5/sqrt(3),$fn=3);
rotate([0, -b, -c+180]) cylinder(3, r=0.5/sqrt(3),$fn=3);
};
sphere(1.6);
};
intersection(){
difference(){
sphere(1.8);
sphere(1.6);
};
rotate([180, b, c]) hull(){
translate([t,0,0]) cylinder(h,r,r);
rotate([0,0,120]) translate([t,0,0]) cylinder(h,r,r);
rotate([0,0,-120]) translate([t,0,0]) cylinder(h,r,r);
};
};
intersection(){
difference(){
sphere(1.8);
sphere(1.6);
};
rotate([180, b, -c]) hull(){
translate([t,0,0]) cylinder(h,r,r);
rotate([0,0,120]) translate([t,0,0]) cylinder(h,r,r);
rotate([0,0,-120]) translate([t,0,0]) cylinder(h,r,r);
};
};
intersection(){
difference(){
sphere(1.8);
sphere(1.6);
};
rotate([0, -b+180, -c]) hull(){
translate([t,0,0]) cylinder(h,r,r);
rotate([0,0,120]) translate([t,0,0]) cylinder(h,r,r);
rotate([0,0,-120]) translate([t,0,0]) cylinder(h,r,r);
};
};
intersection(){
difference(){
sphere(1.8);
sphere(1.6);
};
rotate([0, -b+180, c]) hull(){
translate([t,0,0]) cylinder(h,r,r);
rotate([0,0,120]) translate([t,0,0]) cylinder(h,r,r);
rotate([0,0,-120]) translate([t,0,0]) cylinder(h,r,r);
};
};
intersection(){
difference(){
sphere(1.8);
sphere(1.6);
};
rotate([0, -b, -c]) hull(){
translate([t,0,0]) cylinder(h,r,r);
rotate([0,0,120]) translate([t,0,0]) cylinder(h,r,r);
rotate([0,0,-120]) translate([t,0,0]) cylinder(h,r,r);
};
};
intersection(){
difference(){
sphere(1.8);
sphere(1.6);
};
rotate([0, -b, c]) hull(){
translate([t,0,0]) cylinder(h,r,r);
rotate([0,0,120]) translate([t,0,0]) cylinder(h,r,r);
rotate([0,0,-120]) translate([t,0,0]) cylinder(h,r,r);
};
};
intersection(){
difference(){
sphere(1.8);
sphere(1.6);
};
rotate([0, -b, c+180]) hull(){
translate([t,0,0]) cylinder(h,r,r);
rotate([0,0,120]) translate([t,0,0]) cylinder(h,r,r);
rotate([0,0,-120]) translate([t,0,0]) cylinder(h,r,r);
};
};
intersection(){
difference(){
sphere(1.8);
sphere(1.6);
};
rotate([0, -b, -c+180]) hull(){
translate([t,0,0]) cylinder(h,r,r);
rotate([0,0,120]) translate([t,0,0]) cylinder(h,r,r);
rotate([0,0,-120]) translate([t,0,0]) cylinder(h,r,r);
};
};
};
q=1.8;
coin();Pour les faces nous avons :
module face(){
w=0.47;
k=0.65;
difference(){
intersection(){
union(){
hull(){
translate([k,k,0]) cylinder(4.7,w,w,center=true);
translate([-k,k,0]) cylinder(4.7,w,w,center=true);
translate([k,-k,0]) cylinder(4.7,w,w,center=true);
translate([-k,-k,0])cylinder(4.7,w,w,center=true);
};
rotate([90,0,0]) hull(){
translate([k,k,0]) cylinder(4.7,w,w,center=true);
translate([-k,k,0]) cylinder(4.7,w,w,center=true);
translate([k,-k,0]) cylinder(4.7,w,w,center=true);
translate([-k,-k,0])cylinder(4.7,w,w,center=true);
};
rotate([0,90,0]) hull(){
translate([k,k,0]) cylinder(4.7,w,w,center=true);
translate([-k,k,0]) cylinder(4.7,w,w,center=true);
translate([k,-k,0]) cylinder(4.7,w,w,center=true);
translate([-k,-k,0])cylinder(4.7,w,w,center=true);
};
};
sphere(2.4);
};
sphere(2.25);
};
difference(){
union(){
cube([5,1.7,1.7],center=true);
cube([1.7,5,1.7],center=true);
cube([1.7,1.7,5],center=true);
};
sphere(2.25);
};
};
face();Et enfin les cotécotés :


module cote(){
difference(){
union(){
cube([0.9,3.7,3.7],center=true);
cube([3.7,0.9,3.7],center=true);
cube([3.7,3.7,0.9],center=true);
};
union(){
cube([1,1,3.8],center=true);
cube([3.8,1,1],center=true);
cube([1,3.8,1],center=true);
sphere(1.6);
};
};
//rotate([45,0,0]) cube([3,1,3],center=true);
intersection(){
difference(){
union(){
rotate([45,0,0]) cube([2.1,0.9,5],center=true); //rectangles initiaux
rotate([-45,0,0]) cube([2.1,0.9,5],center=true);
rotate([0,45,0]) cube([0.9,2.1,5],center=true);
rotate([0,-45,0]) cube([0.9,2.1,5],center=true);
rotate([0,0,45]) cube([5,0.9,2.1],center=true);
rotate([0,0,-45]) cube([5,0.9,2.1],center=true);
};
union(){
rotate([45,0,0]) cube([1.7,1.3,4.1],center=true);
rotate([-45,0,0]) cube([1.7,1.3,4.1],center=true);
rotate([0,45,0]) cube([1.3,1.7,4.1],center=true);
rotate([0,-45,0]) cube([1.3,1.7,4.1],center=true);
rotate([0,0,45]) cube([4.1,1.3,1.7],center=true);
rotate([0,0,-45]) cube([4.1,1.3,1.7],center=true);
};
union(){
rotate([45,0,0]) cube([1.9,1.2,3.8],center=true);
rotate([-45,0,0]) cube([1.9,1.2,3.8],center=true);
rotate([0,45,0]) cube([1.2,1.9,3.8],center=true);
rotate([0,-45,0]) cube([1.2,1.9,3.8],center=true);
rotate([0,0,45]) cube([3.8,1.2,1.9],center=true);
rotate([0,0,-45]) cube([3.8,1.2,1.9],center=true);
};
sphere(2.2);
rotate([-45,0,0]) cube([4.2,0.1,3.1],center=true); //séséparation des parties
rotate([45,0,0]) cube([4.2,0.1,3.1],center=true);
rotate([0,0,45]) cube([3.1,0.1,4.2],center=true);
rotate([0,0,-45]) cube([3.1,0.1,4.2],center=true);
rotate([0,45,0]) cube([0.1,4.2,3.1],center=true);
rotate([0,-45,0]) cube([0.1,4.2,3.1],center=true);
};
sphere(2.4);
};
};
cote(); Ensuite il a fallu dédécouper une pièpièce appartenant àà la pièpièce centrale pour pouvoir remonter le Rubik's cube aprèaprès l'impression.
module centre(){ //piece de centre
for(i=[0:3]){
translate([5,i,0]) intersection() {
union(){
translate([0,.0]) difference(){ //sphere creusécreusée et trouétroué
sphere(1.5);
sphere(1.2);
rotate([90,0,0]) cylinder(h=16,r=0.5,center=true);
rotate([0,90,0]) cylinder(h=16,r=0.5,center=true);
rotate([0,0,90]) cylinder(h=16,r=0.5,center=true);
rotate([90,0,0])translate([0.95,0.95,0]) cylinder(0.5,0.1,0.1,center=true);
rotate([90,0,0])translate([-0.95,0.95,0]) cylinder(0.5,0.1,0.1,center=true);
};
};
translate([-8,-10,0]) cube(10);
};
translate([5.95,-0.95+i,0]) cylinder(0.5,0.08,0.08,center=true);
translate([4.05,-0.95+i,0]) cylinder(0.5,0.08,0.08,center=true);
};
difference(){ //Axe de rotation des faces
union(){
sphere(1.1);
rotate([90,0,0]) cylinder(h=5,r=0.4,center=true);
rotate([0,90,0]) cylinder(h=5,r=0.4,center=true);
rotate([0,0,90]) cylinder(h=5,r=0.4,center=true);
};
sphere(0.9);
cube(1.6,center=true);
};
sphere(0.8); //sphere pour callécallé les axes
};
centre(); Ce n'est pas trètrès visible mais le but de chaque morceaux est que toute les pièpièces se maintiennent les une les autres et ainsi que l'ont puisse les bouger entre elles alors qu'elles ne sont pas collécollées.
Le code entier du Rubik's cube est le suivant :
module centre(){ //piece de centre
for(i=[0:3]){
translate([5,i,0]) intersection() {
union(){
translate([0,.0]) difference(){ //sphere creusécreusée et trouétroué
sphere(1.5);
sphere(1.2);
rotate([90,0,0]) cylinder(h=16,r=0.5,center=true);
rotate([0,90,0]) cylinder(h=16,r=0.5,center=true);
rotate([0,0,90]) cylinder(h=16,r=0.5,center=true);
rotate([90,0,0])translate([0.95,0.95,0]) cylinder(0.5,0.1,0.1,center=true);
rotate([90,0,0])translate([-0.95,0.95,0]) cylinder(0.5,0.1,0.1,center=true);
};
};
translate([-8,-10,0]) cube(10);
};
translate([5.95,-0.95+i,0]) cylinder(0.5,0.08,0.08,center=true);
translate([4.05,-0.95+i,0]) cylinder(0.5,0.08,0.08,center=true);
};
difference(){ //Axe de rotation des faces
union(){
sphere(1.1);
rotate([90,0,0]) cylinder(h=5,r=0.4,center=true);
rotate([0,90,0]) cylinder(h=5,r=0.4,center=true);
rotate([0,0,90]) cylinder(h=5,r=0.4,center=true);
};
sphere(0.9);
cube(1.6,center=true);
};
sphere(0.8); //sphere pour callécallé les axes
};
// cube(1.75,center=true);
//sphere(0.8); //sphere pour callécallé les axes
module cube_plein(){ //Toutes les pieces
for(i=[-1.8:1.8:1.8], j=[-1.8:1.8:1.8], k=[-1.8:1.8:1.8]) {
translate([i,j,k]) intersection(){
cube(1.7, center=true);
sphere(1.3);
};
};
};
module total(){
difference(){
cube_plein();
union(){
extrude_cote(); //creusage des pieces de cotécoté
rotate([90,0,0]) extrude_cote();
rotate([0,90,0]) extrude_cote();
rotate([0,0,90]) extrude_cote();
rotate([90,0,90]) extrude_cote();
rotate([90,90,0]) extrude_cote();
sphere(2.45); //Zone de la piece centrale
};
};
};
module coin(){
q=1.8;
//translate([q,q,q]) cube(1.29,center=true);
translate([q,q,-q]) cube(1.29,center=true);
translate([q,-q,q]) cube(1.29,center=true);
translate([q,-q,-q]) cube(1.29,center=true);
translate([-q,q,q]) cube(1.29,center=true);
translate([-q,q,-q]) cube(1.29,center=true);
translate([-q,-q,q]) cube(1.29,center=true);
translate([-q,-q,-q]) cube(1.29,center=true);
x= 1.21/sqrt(3); y = 1.21/sqrt(3); z = 1.21/sqrt(3); // point coordinates of end of cylinder
length = norm([x,y,z]); // radial distance
b = acos(z/length); // inclination angle
c = atan2(y,x); // azimuthal angle
h=5;
r=0.2;
t=0.5;
difference(){
union(){
rotate([180, b, c]) cylinder(3, r=0.5/sqrt(3),$fn=3);
rotate([180, b, -c]) cylinder(3, r=0.5/sqrt(3),$fn=3);
rotate([0, -b+180, c]) cylinder(3, r=0.5/sqrt(3),$fn=3);
rotate([0, -b+180, -c]) cylinder(3, r=0.5/sqrt(3),$fn=3);
rotate([0, -b, -c]) cylinder(3, r=0.5/sqrt(3),$fn=3);
rotate([0, -b, c]) cylinder(3, r=0.5/sqrt(3),$fn=3);
rotate([0, -b, c+180]) cylinder(3, r=0.5/sqrt(3),$fn=3);
rotate([0, -b, -c+180]) cylinder(3, r=0.5/sqrt(3),$fn=3);
};
sphere(1.6);
};
intersection(){
difference(){
sphere(1.8);
sphere(1.6);
};
rotate([180, b, c]) hull(){
translate([t,0,0]) cylinder(h,r,r);
rotate([0,0,120]) translate([t,0,0]) cylinder(h,r,r);
rotate([0,0,-120]) translate([t,0,0]) cylinder(h,r,r);
};
};
intersection(){
difference(){
sphere(1.8);
sphere(1.6);
};
rotate([180, b, -c]) hull(){
translate([t,0,0]) cylinder(h,r,r);
rotate([0,0,120]) translate([t,0,0]) cylinder(h,r,r);
rotate([0,0,-120]) translate([t,0,0]) cylinder(h,r,r);
};
};
intersection(){
difference(){
sphere(1.8);
sphere(1.6);
};
rotate([0, -b+180, -c]) hull(){
translate([t,0,0]) cylinder(h,r,r);
rotate([0,0,120]) translate([t,0,0]) cylinder(h,r,r);
rotate([0,0,-120]) translate([t,0,0]) cylinder(h,r,r);
};
};
intersection(){
difference(){
sphere(1.8);
sphere(1.6);
};
rotate([0, -b+180, c]) hull(){
translate([t,0,0]) cylinder(h,r,r);
rotate([0,0,120]) translate([t,0,0]) cylinder(h,r,r);
rotate([0,0,-120]) translate([t,0,0]) cylinder(h,r,r);
};
};
intersection(){
difference(){
sphere(1.8);
sphere(1.6);
};
rotate([0, -b, -c]) hull(){
translate([t,0,0]) cylinder(h,r,r);
rotate([0,0,120]) translate([t,0,0]) cylinder(h,r,r);
rotate([0,0,-120]) translate([t,0,0]) cylinder(h,r,r);
};
};
intersection(){
difference(){
sphere(1.8);
sphere(1.6);
};
rotate([0, -b, c]) hull(){
translate([t,0,0]) cylinder(h,r,r);
rotate([0,0,120]) translate([t,0,0]) cylinder(h,r,r);
rotate([0,0,-120]) translate([t,0,0]) cylinder(h,r,r);
};
};
intersection(){
difference(){
sphere(1.8);
sphere(1.6);
};
rotate([0, -b, c+180]) hull(){
translate([t,0,0]) cylinder(h,r,r);
rotate([0,0,120]) translate([t,0,0]) cylinder(h,r,r);
rotate([0,0,-120]) translate([t,0,0]) cylinder(h,r,r);
};
};
intersection(){
difference(){
sphere(1.8);
sphere(1.6);
};
rotate([0, -b, -c+180]) hull(){
translate([t,0,0]) cylinder(h,r,r);
rotate([0,0,120]) translate([t,0,0]) cylinder(h,r,r);
rotate([0,0,-120]) translate([t,0,0]) cylinder(h,r,r);
};
};
};
q=1.8;
//coin();
module extrude_cote(){
difference(){
cube([1.9,4.5,2.7],center=true);
translate([0,1.8,0]) cube(1.7,center=true);
translate([0,-1.7,0]) cube(1.9,center=true);
};
};
/*extrude_cote();
rotate([90,0,0]) extrude_cote();
rotate([0,90,0]) extrude_cote();
rotate([0,0,90]) extrude_cote();
rotate([90,0,90]) extrude_cote();
rotate([90,90,0]) extrude_cote();*/
difference(){
union() {
centre();
total();
cote();
face();
coin();
};
//translate([0.9,0.9,0.9]) cube(10);
};
module face(){
w=0.47;
k=0.65;
difference(){
intersection(){
union(){
hull(){
translate([k,k,0]) cylinder(4.7,w,w,center=true);
translate([-k,k,0]) cylinder(4.7,w,w,center=true);
translate([k,-k,0]) cylinder(4.7,w,w,center=true);
translate([-k,-k,0])cylinder(4.7,w,w,center=true);
};
rotate([90,0,0]) hull(){
translate([k,k,0]) cylinder(4.7,w,w,center=true);
translate([-k,k,0]) cylinder(4.7,w,w,center=true);
translate([k,-k,0]) cylinder(4.7,w,w,center=true);
translate([-k,-k,0])cylinder(4.7,w,w,center=true);
};
rotate([0,90,0]) hull(){
translate([k,k,0]) cylinder(4.7,w,w,center=true);
translate([-k,k,0]) cylinder(4.7,w,w,center=true);
translate([k,-k,0]) cylinder(4.7,w,w,center=true);
translate([-k,-k,0])cylinder(4.7,w,w,center=true);
};
};
sphere(2.4);
};
sphere(2.25);
};
difference(){
union(){
cube([5,1.7,1.7],center=true);
cube([1.7,5,1.7],center=true);
cube([1.7,1.7,5],center=true);
};
sphere(2.25);
};
};
//face();
module cote(){
difference(){
union(){
cube([0.9,3.7,3.7],center=true);
cube([3.7,0.9,3.7],center=true);
cube([3.7,3.7,0.9],center=true);
};
union(){
cube([1,1,3.8],center=true);
cube([3.8,1,1],center=true);
cube([1,3.8,1],center=true);
sphere(1.6);
};
};
//rotate([45,0,0]) cube([3,1,3],center=true);
intersection(){
difference(){
union(){
rotate([45,0,0]) cube([2.1,0.9,5],center=true); //rectangles initiaux
rotate([-45,0,0]) cube([2.1,0.9,5],center=true);
rotate([0,45,0]) cube([0.9,2.1,5],center=true);
rotate([0,-45,0]) cube([0.9,2.1,5],center=true);
rotate([0,0,45]) cube([5,0.9,2.1],center=true);
rotate([0,0,-45]) cube([5,0.9,2.1],center=true);
};
union(){
rotate([45,0,0]) cube([1.7,1.3,4.1],center=true);
rotate([-45,0,0]) cube([1.7,1.3,4.1],center=true);
rotate([0,45,0]) cube([1.3,1.7,4.1],center=true);
rotate([0,-45,0]) cube([1.3,1.7,4.1],center=true);
rotate([0,0,45]) cube([4.1,1.3,1.7],center=true);
rotate([0,0,-45]) cube([4.1,1.3,1.7],center=true);
};
union(){
rotate([45,0,0]) cube([1.9,1.2,3.8],center=true);
rotate([-45,0,0]) cube([1.9,1.2,3.8],center=true);
rotate([0,45,0]) cube([1.2,1.9,3.8],center=true);
rotate([0,-45,0]) cube([1.2,1.9,3.8],center=true);
rotate([0,0,45]) cube([3.8,1.2,1.9],center=true);
rotate([0,0,-45]) cube([3.8,1.2,1.9],center=true);
};
sphere(2.2);
rotate([-45,0,0]) cube([4.2,0.1,3.1],center=true); //séséparation des parties
rotate([45,0,0]) cube([4.2,0.1,3.1],center=true);
rotate([0,0,45]) cube([3.1,0.1,4.2],center=true);
rotate([0,0,-45]) cube([3.1,0.1,4.2],center=true);
rotate([0,45,0]) cube([0.1,4.2,3.1],center=true);
rotate([0,-45,0]) cube([0.1,4.2,3.1],center=true);
};
sphere(2.4);
};
};
x= 1.21/sqrt(3); y = 1.21/sqrt(3); z = 1.21/sqrt(3); // point coordinates of end of cylinder
length = norm([x,y,z]); // radial distance
b = acos(z/length); // inclination angle
c = atan2(y,x); // azimuthal angle
h=5;
r=0.2;
t=0.5;
Et voici le fichier STL : Rubik's cube 2_test4.stl
Une premièpremière impression a échouééchoué surement àà cause d'une courroie qui a sautésauté un cran (problèproblème totalement aléaléatoire).
Projet 2D : porte cléclé
Pour le projet 2D j'ai pensépensé àà faire des portes cléclés.
Il a donc fallu choisir quels dessins graver sur le bois. Mon choix s'est portéporté sur les versions Chibi de personnages tirétirés du manwha Solo Leveling .
Je suis donc parti de l'image suivante.
Il a donc ensuite fallut que je choisisse les personnages qui me plaisait le plus. J'en ai alors choisit quatre: 

Igris Kaisel Beru Acier
Ensuite, grâgrâce àà l'outil vectorisation de Inkscape, je les ai mis en noir et blanc et j'ai tracétracé les contours ainsi que les trous pour mettre les boucles porte les accrocher sur un trousseau de cléclé.
Lien du fichier : Porte cléclé Solo Leveling.svg