PROJET ROB de Maroua, Marco, Yanis

Projet Maranis : Un robot écrivain

Informations

Membres :
- Maroua Hriouit
- Yanis Sadoun
- Marco Grandclaude
Mail:
Polytech ROB 3 Année 2023-2024
7 février 2024 - mai 2024

Contexte et objectifs :

Définition et objectifs du projet : Un robot qui dessine

Dans le cadre de nos études en robotique, on est amené à concevoir un robot capable de dessiner a l’aide d’un crayon fixé à l’extrémité terminale du robot.

L'objectif principal de ce projet consiste à élaborer et mettre en œuvre un système robotique complet, englobant sa composante mécanique, son système de motorisation, son dispositif de commande, ainsi que son interface de pilotage. Le cahier des charges fourni définit de manière détaillée les fonctions que le système doit exécuter et les contraintes auxquelles il doit se conformer.

Pour nous, étudiants, ce projet offre l'opportunité d'acquérir une expérience professionnelle en gestion de projet, en mettant particulièrement l'accent sur le travail en équipe. Il nous permettra également de mettre en pratique tout ce que nous avons étudié tout au long du premier semestre, y compris la conception et la modélisation, le calcul des modèles géométriques direct et inverse, ainsi que la programmation en C. Et enfin apprendre à manipuler des machines d’impression 3D et découpe LASER.

~~CITEZ~~
Lors ~~VOTRE~~de ~~SOURCE~~notre première séance, nos professeurs nous ont fourni une description fonctionnelle détaillée des besoins et contraintes pour notre projet. C'est sur cette base que nous avons construit et développé notre plan de travail. Voici un résumé de ces exigences clés :

Description fonctionnelle des besoins :

1 - Dessin Précis : Le robot doit être capable d'exécuter des dessins précis définies en 10 secondes +/- 0.2 secondes conformément aux spécifications fournies, en respectant les dimensions et les formes définies :

a. Une ligne de 5cm de long,

b. Une ligne pointillée de 5cm de long,

c. Un cercle de 2.5cm de rayon,

d. Un cercle pointillé de 2.5cm de rayon.

2 - Dessiner, en utilisant un crayon fixé à l'extrémité du bras robotique, un motif prédéfini sur le plan de la plaque de support, dans un carré de dimensions 5 cm par 5 cm. Le déplacement du bras robotique sera contrôlé par un joystick. Il est à noter que la figure peut être discontinue, ce qui implique la nécessité de pouvoir soulever le crayon du support horizontal au besoin.

3 - Une fonctionnalité supplémentaire pourrait être mise en œuvre : La possibilité de régler la vitesse de déplacement du robot à travers l'interface.

Moyens à disposition :

- Un crayon

- Interface de commande :

- Une carte arduino UNO avec câble USB-B ;

- Un joystick ;

- Une platine de prototypage ;

- Alimentation régulée 5V ;

- Câbles, LEDs, boutons poussoirs, résistances.

- Motorisation :

- Deux servomoteurs HS422 180° ;

- Un servomoteur Emax ES08A 180°.

- Mécanique :

- Matière PLA pour impression 3D ;

- Feuilles medium : 3mm et 6mm d’épaisseur ;

- Vis et écrous : M2, M2.5, M3, M4.

Roulements et axes de diamètre 4mm.

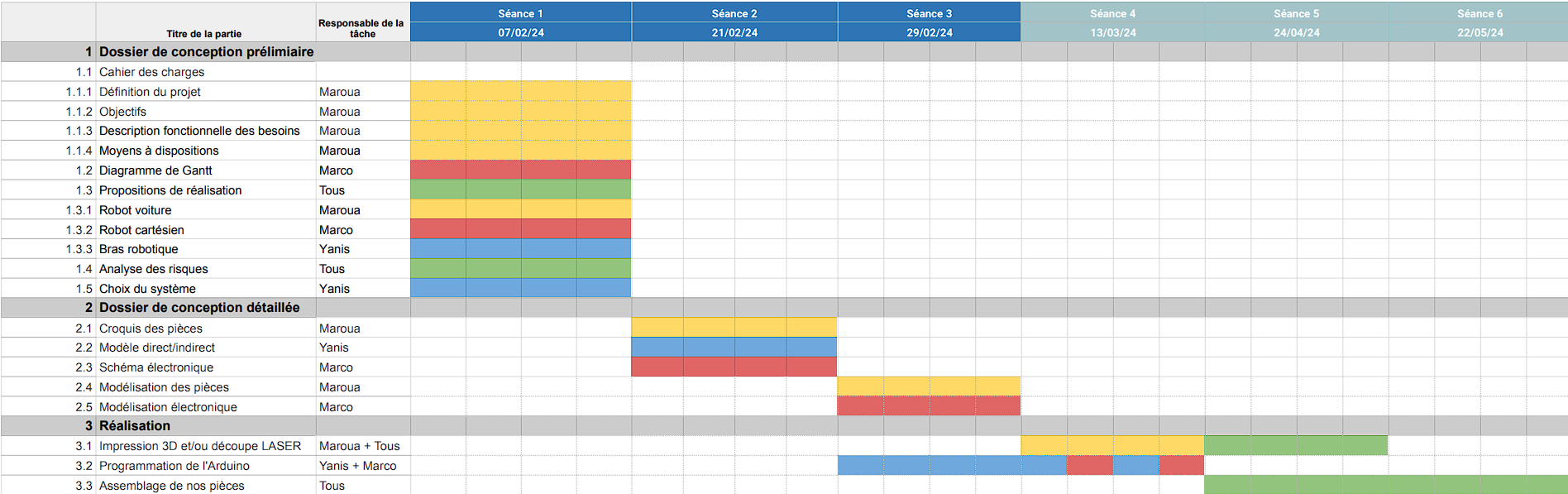
Diagramme de Gantt :

💭 Remarque Importante : Il est important de noter que notre diagramme de Gantt est un outil vivant. Comme le projet progresse, nous pouvons nous attendre à ce qu'il soit ajusté et modifié pour refléter l'évolution de nos plans et la réalité de notre progression. Cette flexibilité nous permettra de rester réactifs et adaptatifs face aux défis et aux opportunités qui se présenteront.

Etape 1 : Propositions de réalisation et analyse des risques 🔍⚙️

Solution 1 : Robot voiture

Principe :

Comme première solution, l'idée consiste d'utiliser une voiture à deux roues sur laquelle seront fixés nos deux moteurs. Ensuite, nous envisageons de positionner une forme cylindrique sur la voiture, à l'intérieur de laquelle sera intégré un engrenage. Cette configuration permettrait la translation du stylo selon l'axe z, offrant ainsi une méthode mécanique pour réaliser les mouvements nécessaires à notre robot.

Croquis :

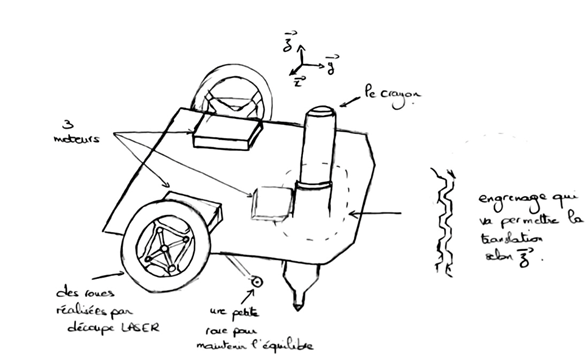
figure 1 : croquis du robot voiture

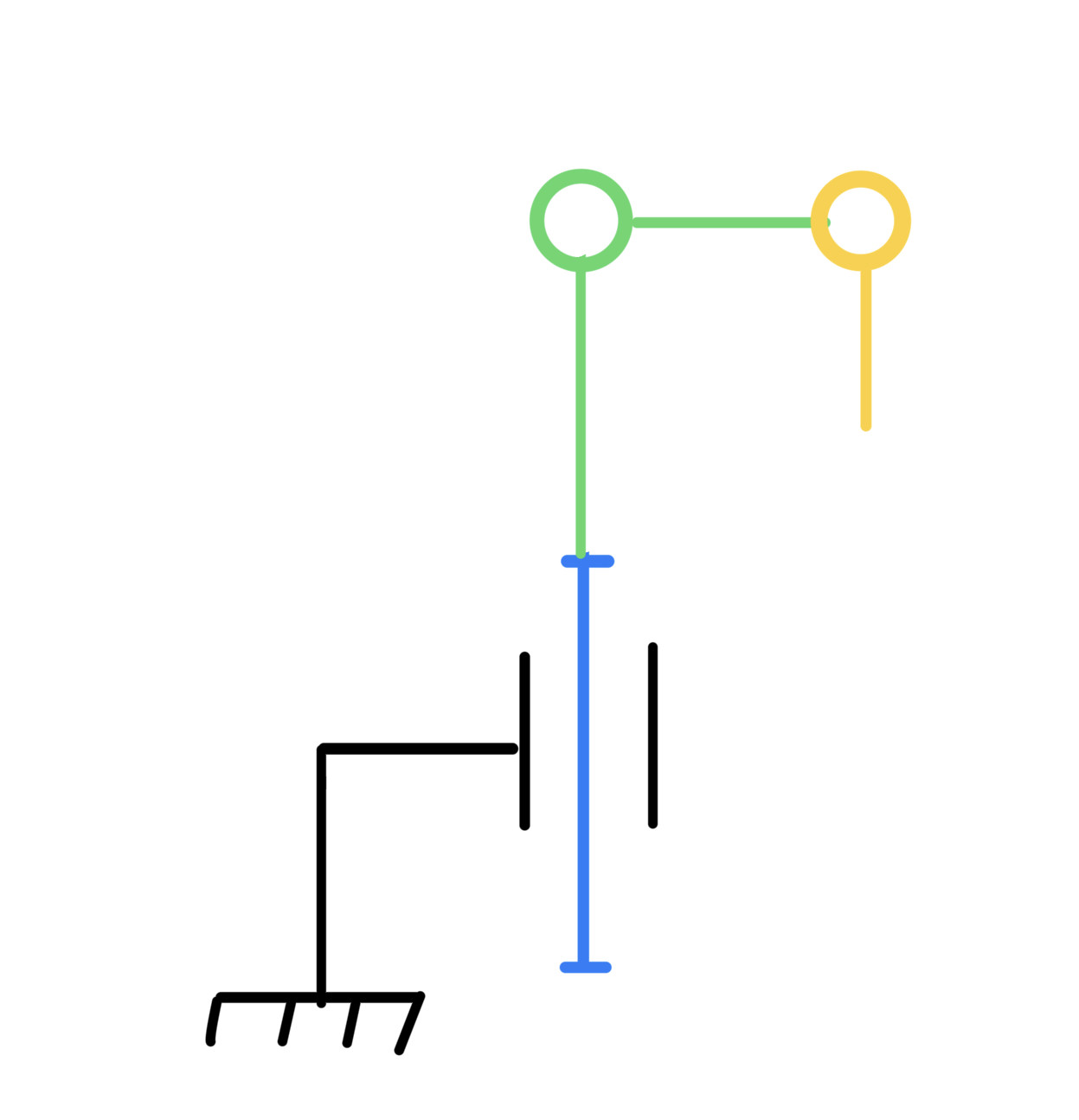
Schéma cinématique :

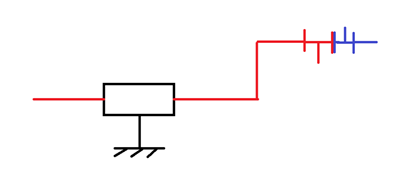figure 2 : schéma cinématique du robot voiture

Contraintes:

Compte tenu des moteurs utilisés, cette solution ne sera pas viable. En effet, les servomoteurs n'effectuent qu'une rotation de 180 degrés, ce qui signifie que pour parcourir une certaine distance D, il faudra effectuer n tours de 360 degrés. Cela nous obligerait à utiliser un diamètre de roues très important, entraînant des complications liées aux calculs et aux glissements.

Solution 2 : robot cartésien

Principe :

Ce robot serait conçu pour se déplacer suivant un système de coordonnées en X et Y, offrant une grande précision dans un espace bidimensionnel.

La particularité de ce robot réside dans sa capacité à effectuer des translations le long de deux axes distincts : horizontal (axe X) et vertical (axe Y). Pour ce faire, le robot serait équipé de rails horizontaux et verticaux, permettant des mouvements fluides et contrôlés dans ces deux directions.

Croquis :

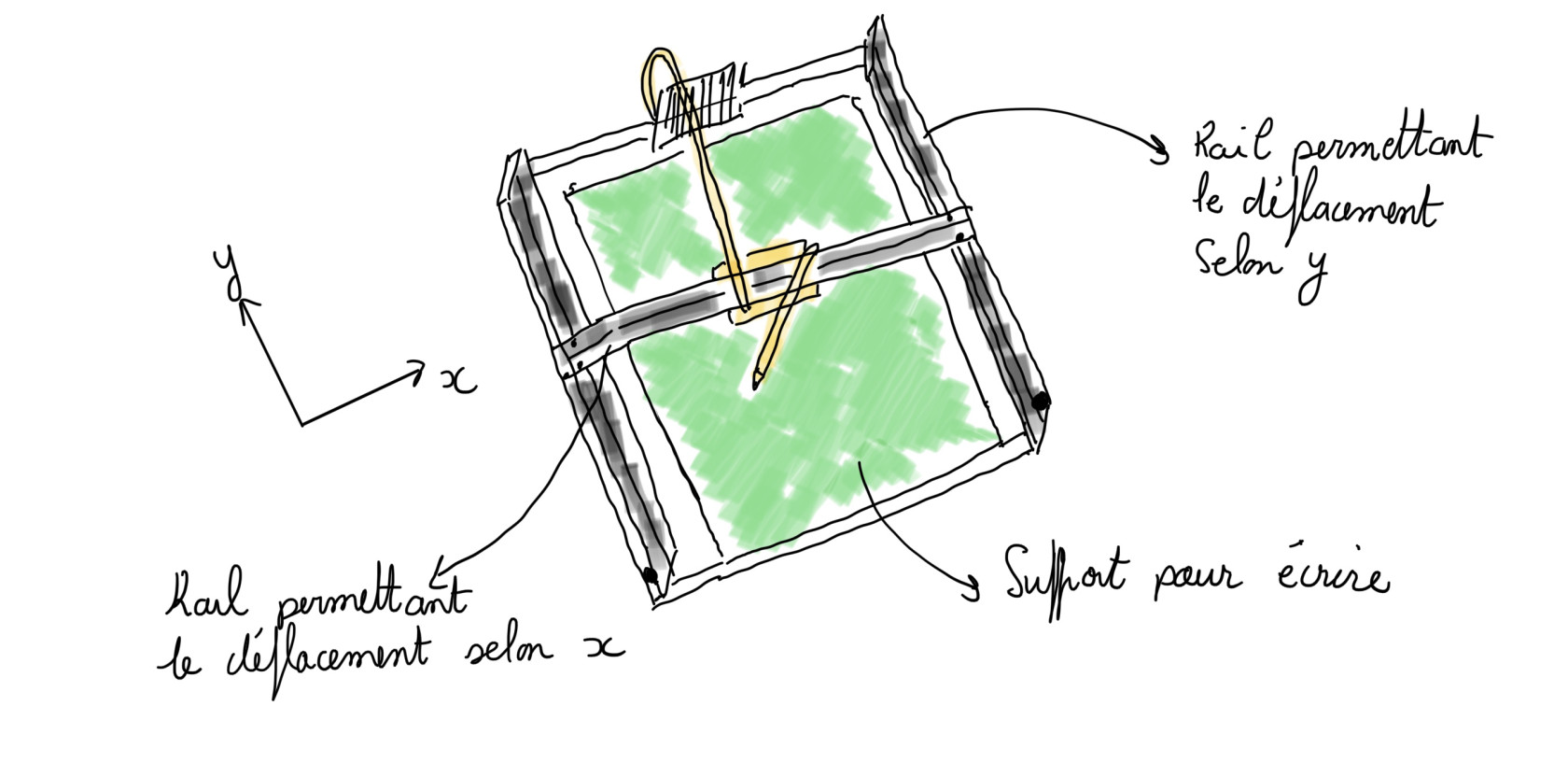
figure 3: croquis du robot cartésien

Schéma cinématique :

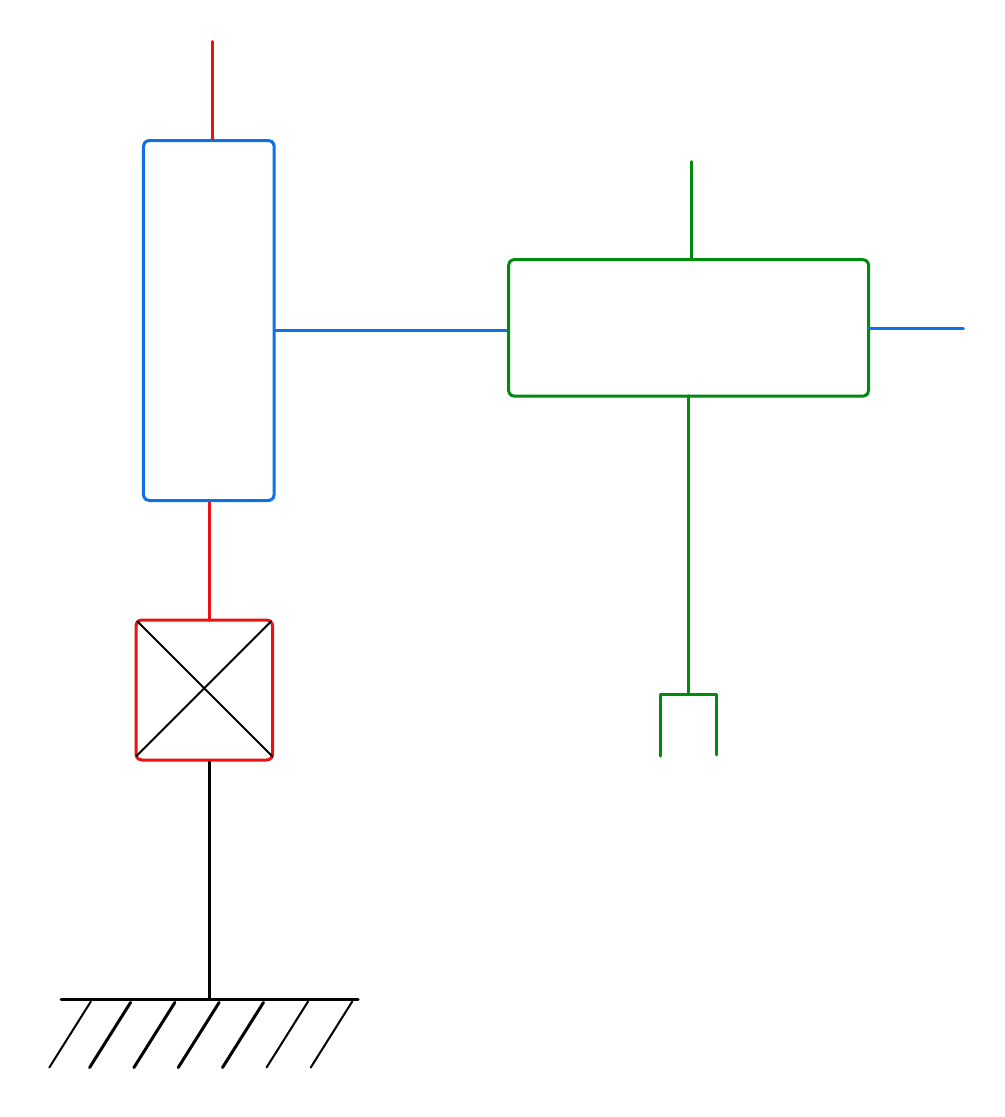
Schéma cinématique Robot cartésien.png

figure 4 : schéma cinématique du robot cartésien

Contraintes :

Manque de matériel pour les translations : Nous ne disposons pas des composants nécessaires, tels que des courroies, pour réaliser les translations efficaces sur les axes X et Y. L'absence de ces éléments essentiels est un obstacle à la construction de ce système .

Complexité de fabrication des rails : La conception et la réalisation des rails, essentiels pour les déplacements précis du robot, nous semblent particulièrement complexes, surtout avec les seuls servomoteurs disponibles.

Incapacité de mouvement sur l'axe Z : Avec les composants actuels, le robot ne serait pas capable de lever le crayon le long de l'axe Z. Cette limitation rend impossible la réalisation de tracés en pointillés, une des exigences clés du cahier des charges.

Bien que conceptuellement intéressante, la solution du robot cartésien se heurte à des contraintes matérielles et techniques qui compromettent sa faisabilité dans notre contexte actuel.

Solution 3 : Robot constitué d'axe en série

Principe :

Le robot envisagé se caractérise par une structure à axe en série. Il intègre un châssis stable comme base principale, sur lequel est fixé un bras articulé. Ce bras se compose de trois segments (bielles), chacun connecté au suivant via une liaison pivot, permettant ainsi une gamme étendue de mouvements. La dernière bielle est directement soudée à un adaptateur, conçu pour maintenir fermement un stylo. La stabilité et la précision du mouvement des bielles seront assurées par l'intégration de roulements. Parallèlement, un support de feuille sera installé, aligné dans le même plan que le châssis du robot, afin de faciliter l'interaction précise du stylo avec le papier.

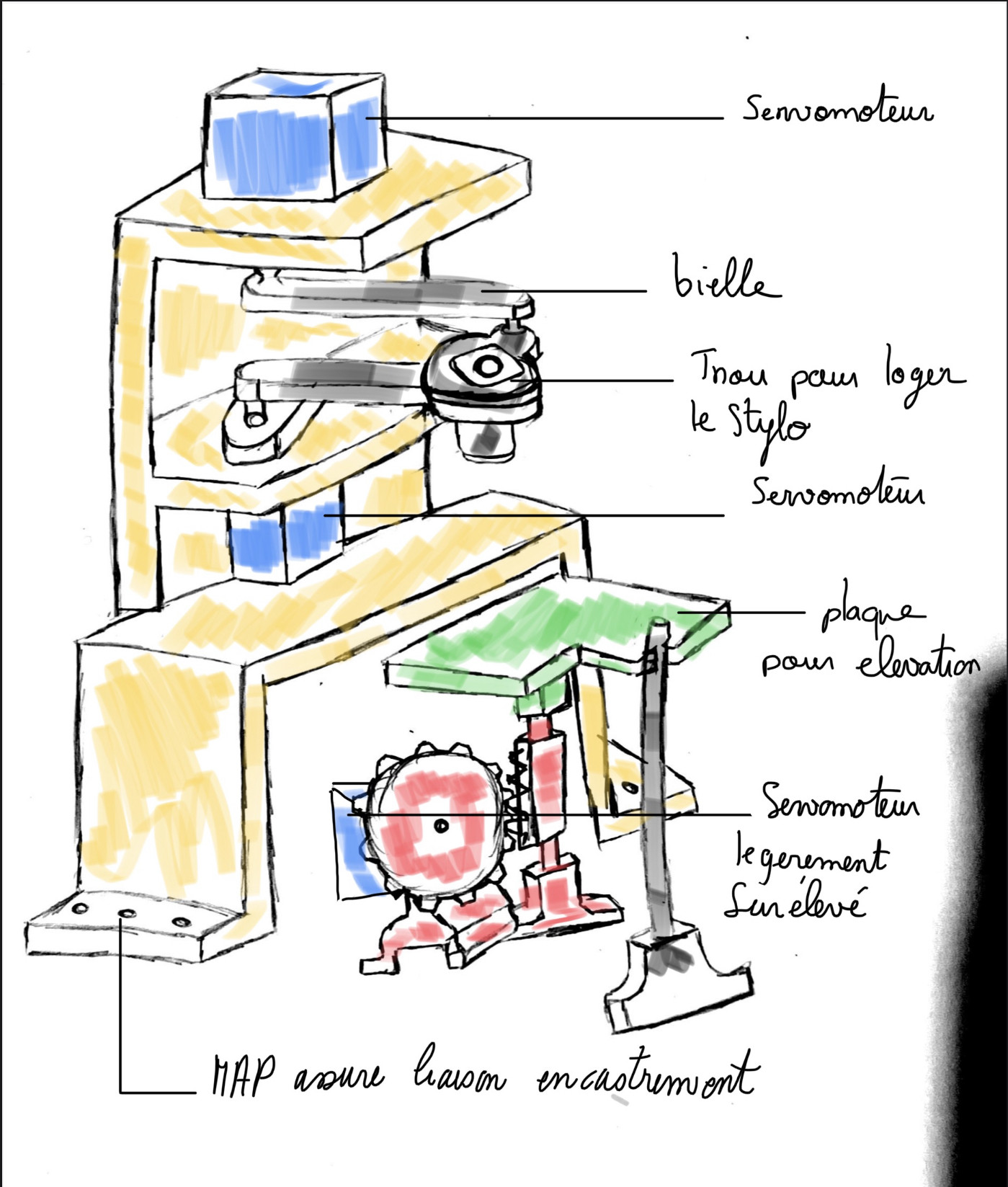
Croquis :

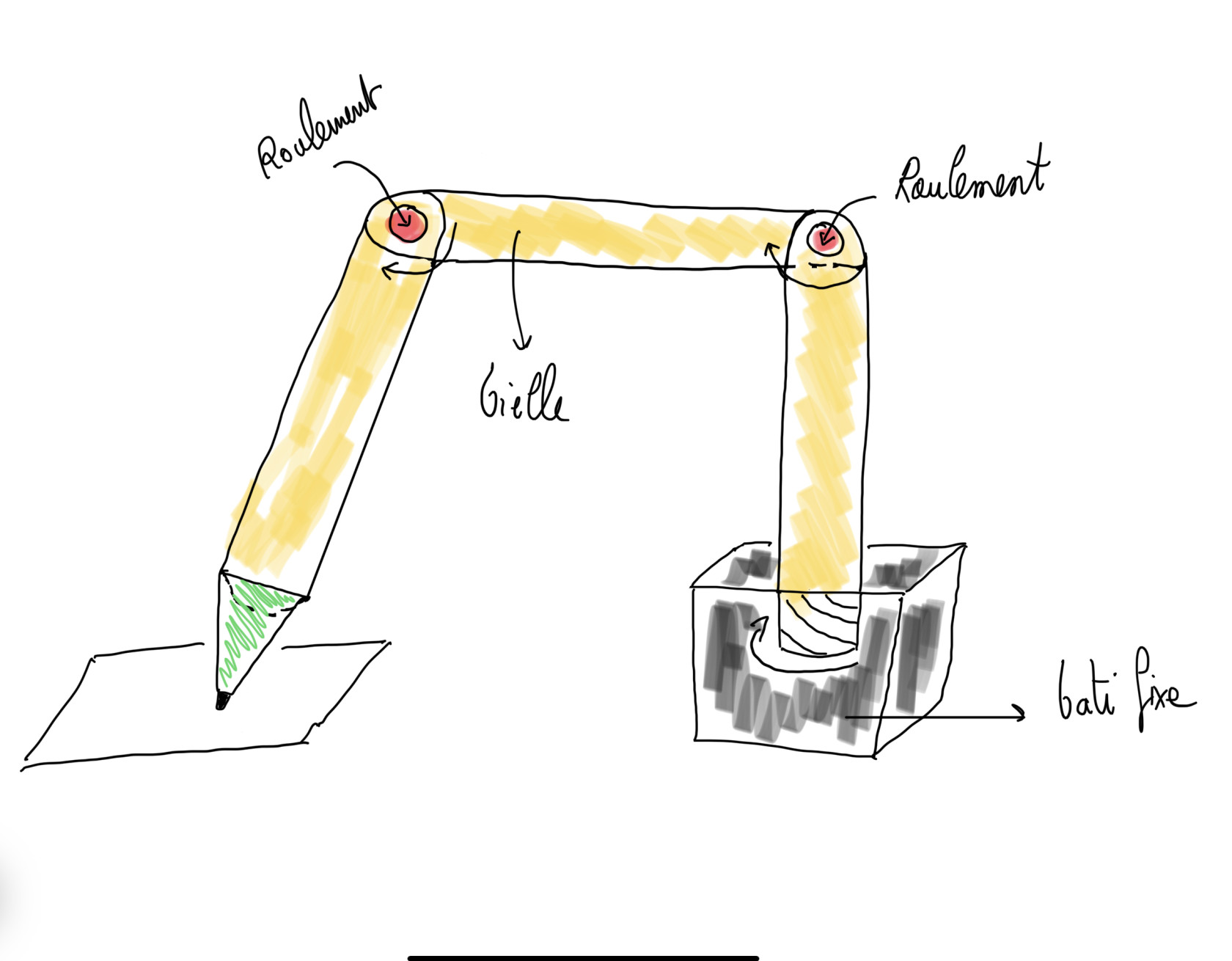
figure 5 : croquis du robot à axe en série

Schéma cinématique :

figure 6 : schéma cinématique du robot à axe en série

Avantages :

Cinématique simple : La structure à axe en série offre une cinématique plus facile à concevoir et à programmer, grâce à une chaîne cinématique linéaire et moins complexe.

Risques et défis :

Stabilité structurelle : Ces robots peuvent présenter des problèmes de stabilité, surtout lors de la manipulation de charges ou lors de mouvements rapides.
Précision dans les positions extrêmes : La précision peut diminuer aux extrémités de la portée du robot, où les effets de la gravité et de la flexion des composants sont plus prononcés.

Solution 4 : Robot à trois rotations

Principe :

Ce concept de robot s'inspire directement de la morphologie humaine, intégrant trois axes de rotation pour imiter les mouvements naturels du corps. En faisant une analogie avec le corps humain, la gestion de la hauteur de la pince (qui agirait comme une main) est assurée par deux rotations principales : une au niveau de l'« épaule » et une autre au niveau du « coude », correspondant respectivement aux rotations 2 et 3 du système. Cette configuration permet une manipulation verticale précise et polyvalente de la pince. Pour compléter la gamme de mouvements, une troisième rotation est ajoutée au niveau du « poignet », offrant la capacité de torsion. Cette troisième rotation apporte une flexibilité supplémentaire, essentielle pour des tâches complexes nécessitant une orientation fine de la pince.

Croquis :

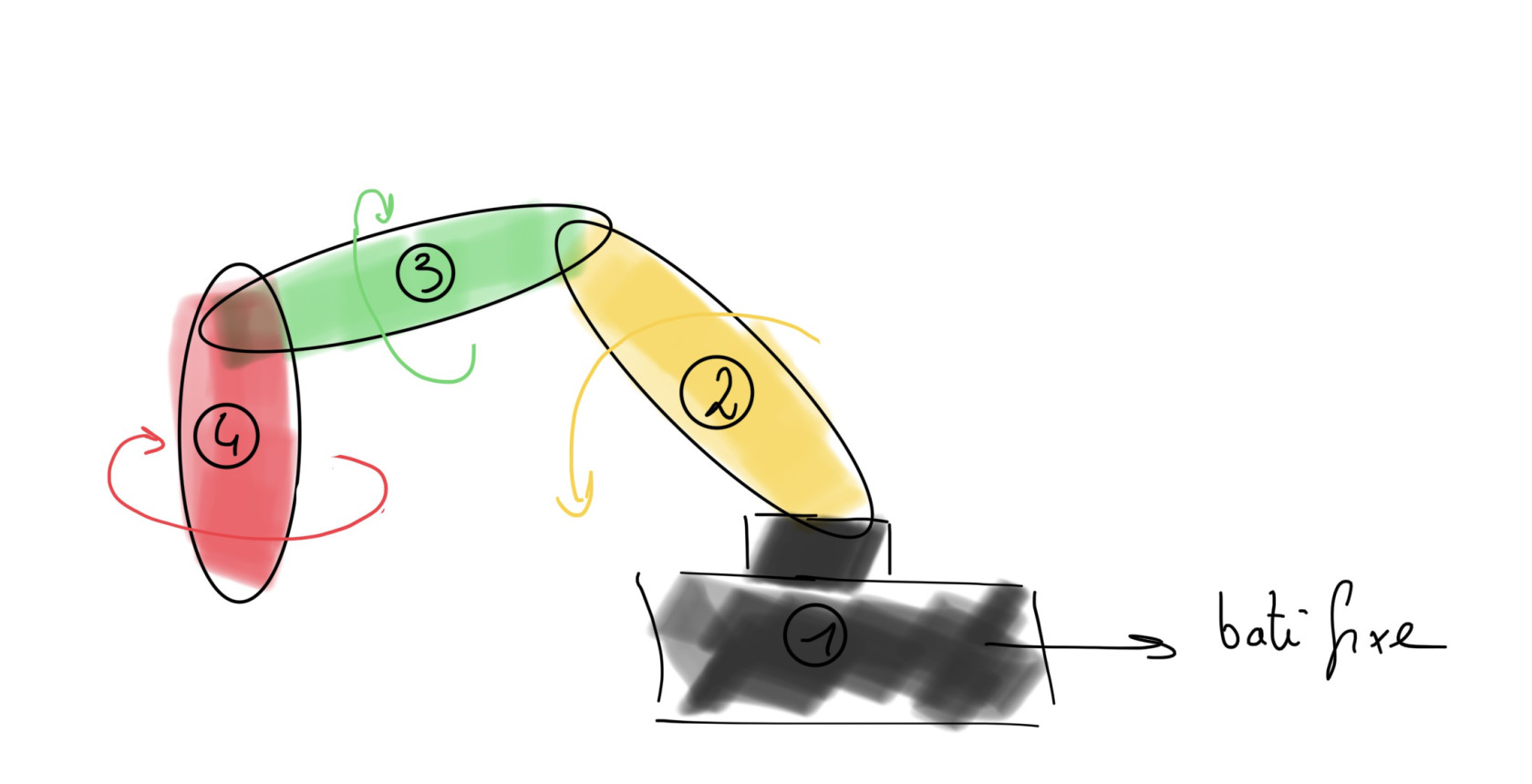
figure 7 : croquis du robot à 3 rotations

Schéma cinématique :

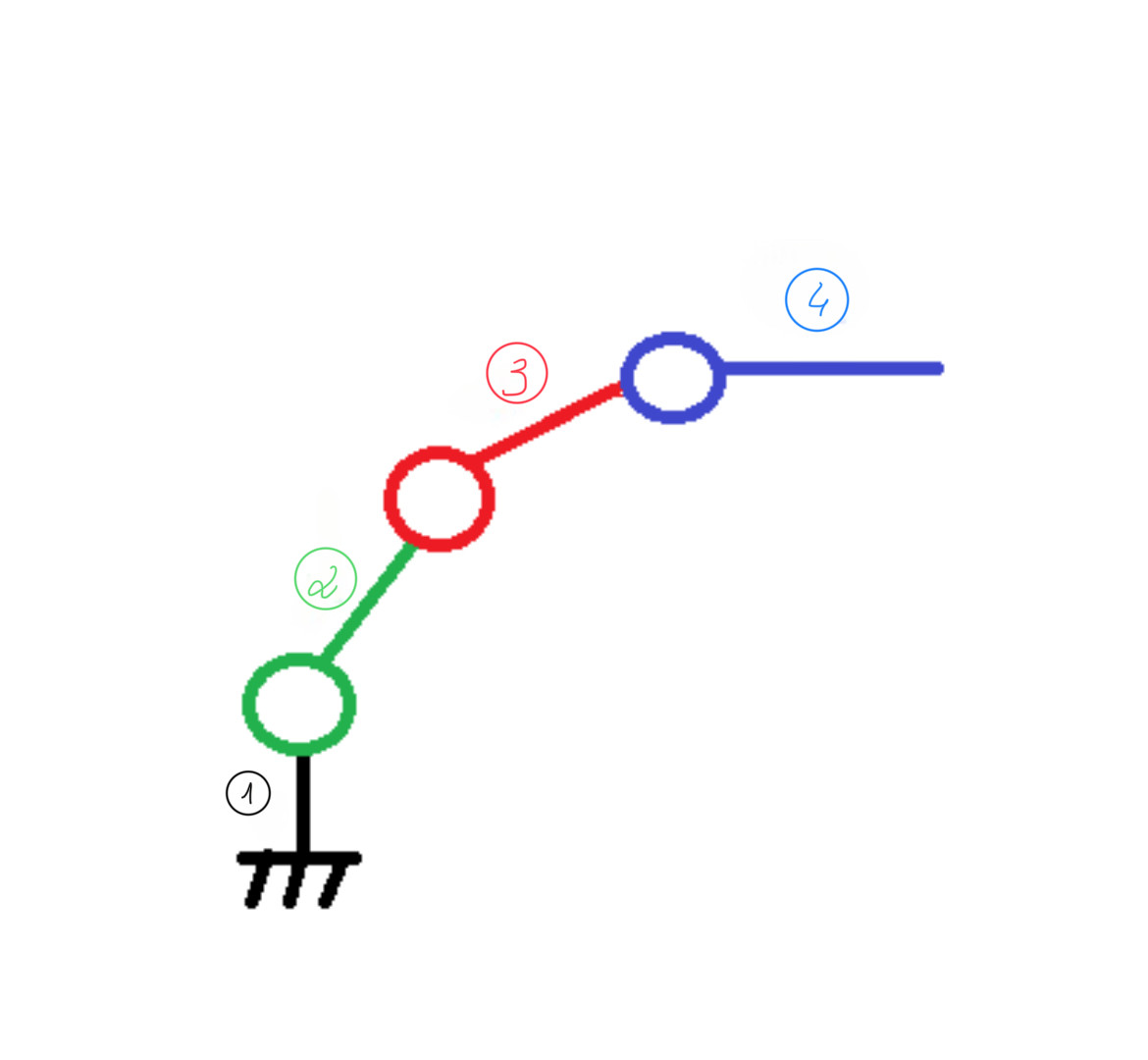
figure 8 : schéma cinématique du robot à trois rotations

Avantages :

Fabrication plus efficace : L’ensemble des pièces peuvent être réalisé en découpe laser ce qui permet une production plus rapide et précise des pièces.

Inconvénients :

Stabilité du stylo : Assurer que le stylo reste précisément à la position voulue durant les mouvements complexes.
Complexité du modèle cinématique inverse : La gestion des trois rotations (épaule, coude, poignet) rend le calcul du modèle cinématique inverse complexe, crucial pour la précision des mouvements du robot.

Solution 5 : Robot avec bras parallèles

Principe :

Le concept envisagé ici est celui d'un robot à bras parallèle à deux axes, conçu spécifiquement pour une manœuvrabilité précise. Pour permettre au stylo de se déplacer verticalement (translation selon l'axe Z), le robot intégrera un mécanisme de pignon -crémaillère. ( Ce choix de conception assure une montée et une descente contrôlées et stables ? C'est quoi une montée stable du stylo. Comme pour le modèle à axe en série, les points de pivot au niveau des "coudes" du robot seront équipés de roulements.

Croquis :

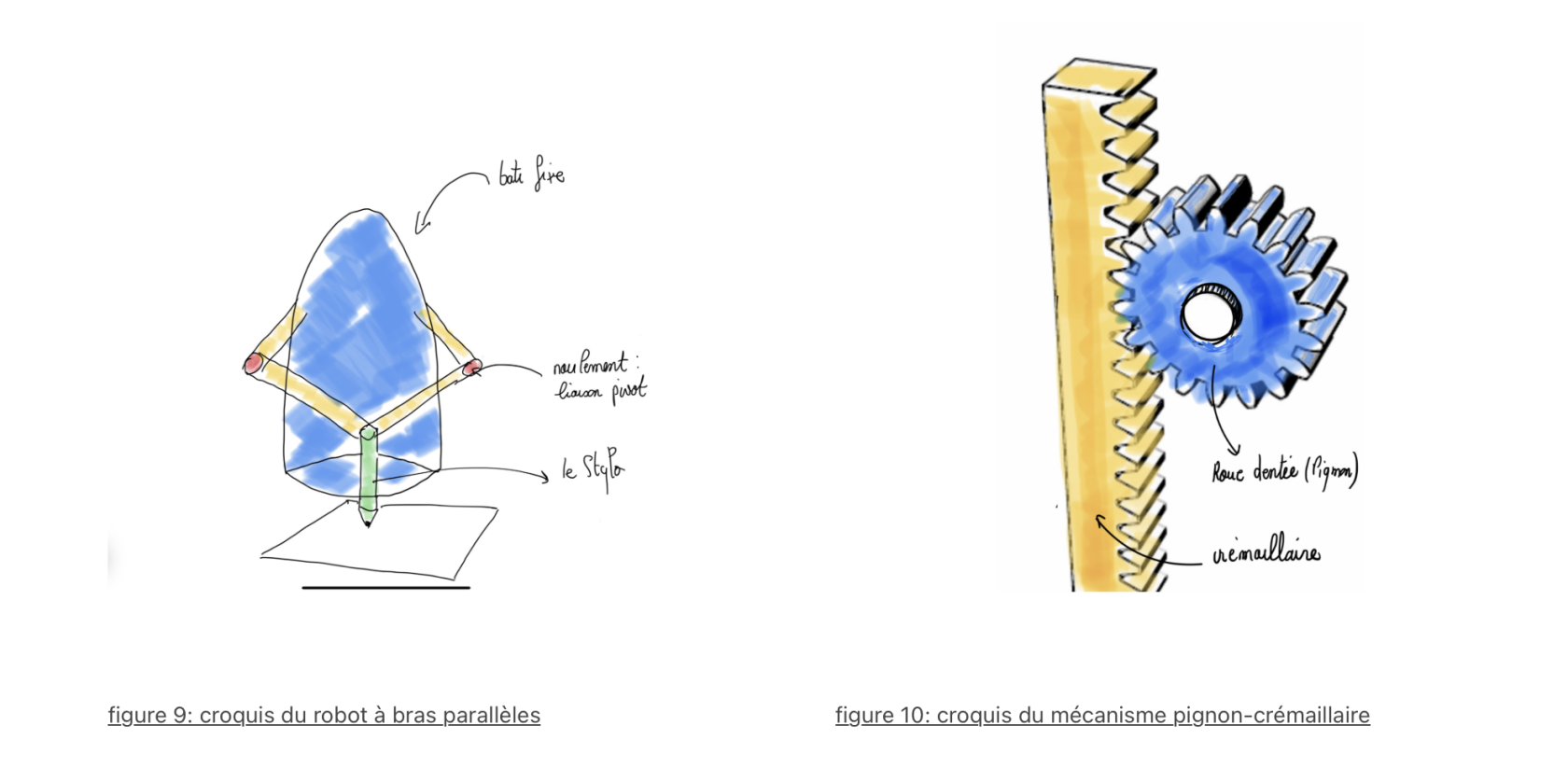
figure 11: croquis détaillé de notre robot à bras parallèles

Schéma cinématique :

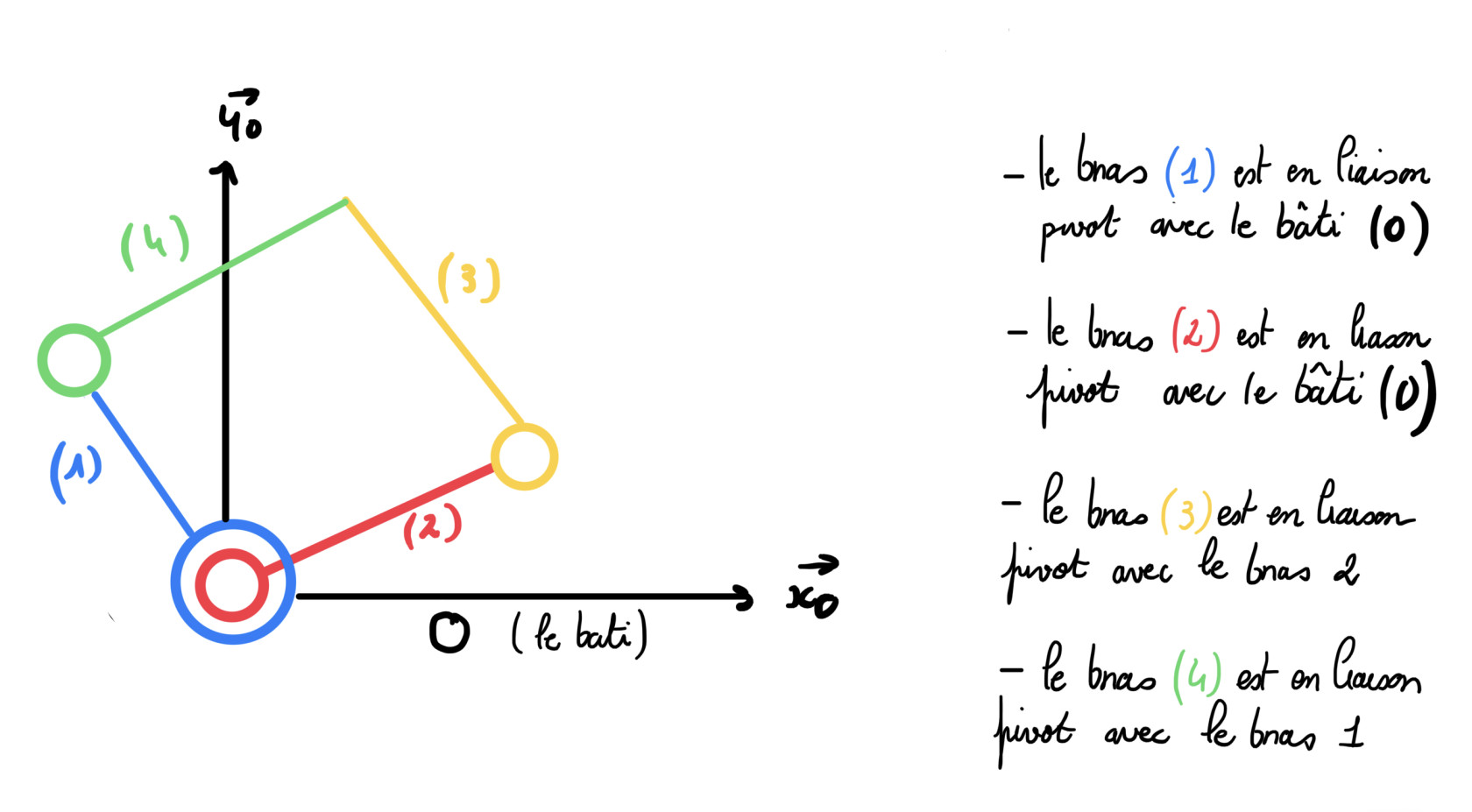
figure 12 : schéma cinématique du robot à bras parallèles

Avantages :

Solidité structurelle : Les robots parallèles offrent une grande solidité et stabilité, ce qui est avantageux pour des tâches nécessitant de la précision et de la force.
Cinématique simplifiée possible : En configurant les bras du robot pour former un parallélogramme avec les axes de servomoteurs alignés, il est possible de simplifier la cinématique, facilitant ainsi la programmation et le contrôle.

Risques et défis:

Complexité cinématique initiale : Sans cette simplification, la cinématique des robots parallèles peut être initialement plus complexe, nécessitant une compréhension approfondie des systèmes mécaniques.

De plus , il faut s’assurer que les rotations des servomoteurs de 180° permettent de couvrir l’ensemble de la surface souhaitée.

Solution retenue

Suite à une analyse approfondie des différentes options, notre équipe a décidé de privilégier la conception d'un robot parallèle pour la suite du projet. Cette décision s'appuie sur plusieurs facteurs clés :

Conformité au cahier des charges : Le robot parallèle répond efficacement aux exigences spécifiées dans le cahier des charges. Sa structure offre la précision et la solidité requises pour les tâches prévues, tout en permettant une gamme de mouvements adaptée à nos besoins.
Faisabilité technique : Avec les composants et les ressources à notre disposition, la réalisation d'un robot parallèle est non seulement possible mais également pratique. La possibilité de simplifier sa cinématique en configurant ses bras en parallélogramme facilite sa programmation et son contrôle, rendant le projet plus gérable dans le cadre de nos contraintes techniques et temporelles.

Nota bene : Le nom de notre robot sera "Maranis"; il est formé en combinant les prénoms Maroua, Marco, et Yanis. Il symbolise l'union de nos efforts et la collaboration au cœur de notre projet...

Etape 2 : calculs Mécaniques 🛠️

À cette étape, nous nous sommes concentrés sur les aspects techniques du projet en abordant la modélisation mécanique appliquée aux bras de notre robot. Notre objectif ? Détailler les modèles géométriques, à la fois direct et inverse, que nous avons développés. En effet, ces modèles sont cruciaux pour préciser la position de l'effecteur du robot, en particulier pour ses mouvements de translation verticale.

L'utilisation de ces modèles géométriques nous offre la capacité de réguler avec exactitude la position et l'orientation de l'effecteur, en se basant sur les angles des articulations. Cette précision est fondamentale pour diverses applications dans les domaines de la robotique et de l'automatique, où la manipulation et le positionnement exacts sont primordiaux.

A - Modélisation du problème

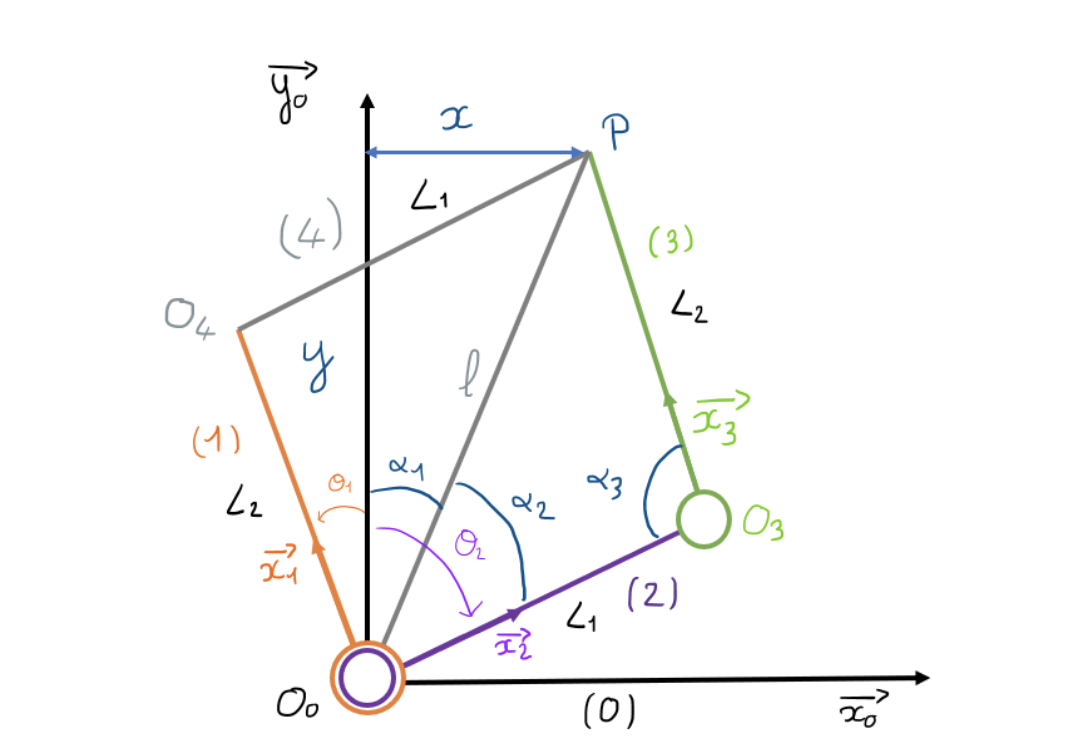
Pasted Graphic.png

figure 13 : schéma cinématique du robot à bras parallèles

Configuration des Moteurs et Simplification Géométrique : Les moteurs de notre robot sont disposés l'un au-dessus de l'autre, mais orientés en sens inverse. Cette configuration particulière permet d'aligner les axes des moteurs, réduisant ainsi l'espace entre deux corps liés et simplifiant de ce fait le modèle géométrique et son inverse. En effet, en alignant les corps opposés à une longueur égale (les quatre bras mesurant la même taille dans notre cas), nous transformons le système en un parallélogramme. Cette transformation apporte plusieurs relations internes utiles au système, liant les angles et les diagonales.

Modélisation et Références du Système : Nous définissons un repère galiléen 𝑅0 = (𝑥0 , 𝑦0 , 𝑧0 ) associé au bâti (0). Le robot est composé de quatre bras : les bras 2 et 4 mesurant une longueur 𝐿1, tandis que les bras 1 et 3 ont une longueur 𝐿2. - Le bras 1 est en liaison pivot autour de l'axe (𝑂0, 𝑧0) avec le bâti. L'angle formé est noté θ1 = (𝑥0, 𝑥1) = (𝑦0, 𝑦1). - Le bras 2, aussi en liaison pivot autour de l'axe (𝑂0, 𝑧0) avec le bâti, a un angle θ2 = (𝑥0, 𝑥2) = (𝑦0, 𝑦2). - Le bras 3 est en liaison pivot autour de l'axe (𝑂3, 𝑧0) avec le bras 2. L'angle α3 = (𝑥2, 𝑥3) = (𝑦2, 𝑦3) est défini, avec le bras 3 restant horizontal et parallèle à l'axe 𝑥0. - Le bras 4, en liaison pivot autour de l'axe (𝑂4, 𝑧0) avec le bras 1, n'est pas visible dans notre modèle simplifié puisque n’intervenant pas dans nos calculs .

L'effecteur du robot se trouve au point P, ayant pour coordonnées (𝑥, 𝑦) dans ce système.

Cette modélisation permet de comprendre clairement la structure mécanique du robot et facilite la programmation et le contrôle de ses mouvements.

B - Modèle géométrique direct

Dans notre projet robotique, nous avons élaboré un modèle géométrique direct qui se base sur des principes de trigonométrie fondamentaux, rendant sa détermination relativement simple. Ce modèle utilise des formules basiques pour calculer les positions du robot.

On rappelle que notre modèle se base sur un parallélogramme. 📐Or, dans un parallélogramme, les côtés opposés sont égaux et les angles adjacents sont complémentaires. De plus, les diagonales se coupent en leur milieu et forment des triangles rectangles avec les côtés du parallélogramme. Nous pouvons donc utiliser ces propriétés pour établir des relations entre les longueurs des bras .

Dès lors :

Pour un robot standard avec des bras de longueurs différentes, les coordonnées x et y de l'effecteur peuvent être exprimées comme suit :

x = L1 sin(θ2) - L2 sin(θ1)

y = L1 cos(θ2) +L2 cos(θ1)

Cependant , nous avons spécifiquement choisi de travailler avec un losange, où ( L = L1 = L2 ). Cette approche réduit la complexité des calculs et permet une meilleure compréhension de la cinématique du robot.

Avec cette simplification, notre modèle géométrique direct se résume à des formules plus simples :

x = L (sin(θ2) - sin(θ1))

y = L (cos(θ2) + cos(θ1))

C- Modèle géométrique Inverse :

L’élaboration du modèle géométrique inverse est une étape essentielle pour le contrôle précis de notre robot. Ce modèle nous permet de calculer les angles nécessaires aux moteurs pour positionner l'effecteur à un point spécifique (x, y) dans l'espace.

Pour commencer, nous avons établi l'angle α1 en utilisant la fonction arctangente, qui est dérivée du rapport entre les côtés opposé et adjacent d'un triangle rectangle formé par les coordonnées de l'effecteur :

α1 =Arctan(x/y)

Ensuite, nous avons appliqué le théorème de Pythagore au triangle rectangle ayant pour longueur 𝑥, 𝑦 𝑒𝑡 𝑙 pour déterminer la longueur de l'hypoténuse l en fonction des coordonnées x et y :

𝑙 = √(x^2+y^2)

En utilisant la propriété fondamentale des triangles selon laquelle la somme des angles internes est égale à 180°, nous avons déduit une relation entre les angles α3 et α2:

α3 = 180°-2*α2 et α2=90°-α3/2

Enfin, grâce à la loi des cosinus ou la formule d'Al-Kashi, nous avons pu exprimer α3 en termes des longueurs des bras L1 , L2 et de l’hypoténuse 𝑙 :

α3= arccos((L1^2+L2^2-𝑙^2)/(2 L1 L2))
Ces relations nous permettent de déterminer les angles des moteurs:

θ1=α2-α1 et θ2=α2+α1

Toutefois, grâce à notre simplification du modèle par un losange; longueur 𝐿 = 𝐿1 = 𝐿2. On obtient les relations suivantes :

α1 =Arctan(x/y)

α2=90°-α3 /2

α3= arcos((2L^2-𝑙^2)/2L^2)

θ1=α2-α1

θ2=α2+α1

Avec ces formules, nous avons en main un système complet qui nous permet de calculer les angles des moteurs pour positionner précisément l'effecteur à un point (x, y) dans l'espace, en considérant les bras de longueur égale.

D - Modélisation de la translation :

Notre mécanisme de translation axiale s'appuie sur un agencement pignon-crémaillère. La crémaillère présente un diamètre de base Bbase 41,25 mm. En prenant en compte un module de conception m de 1,5, nous procédons au calcul du diamètre effectif Deff qui sera utilisé dans les calculs suivants .

Le diamètre effectif est calculé comme suit : Deff = Bbase + 2,5 m=41,25+2,5×1,5=45 mm

Le calcul du diamètre effectif s'appuie sur des données initiales issues de nos premières simulations réalisées sur SolidWorks, en particulier pour le mécanisme pignon-crémaillère. Il est important de noter que ces chiffres, bien que précis dans le cadre de nos simulations initiales sont susceptibles d'évoluer et d'être ajustés au fur et à mesure de l'avancement de notre projet et à mesure que de nouvelles données seront recueillies et analysées.

Le lien entre le nombre de révolutions complètes
Nrev du servomoteur HS-55 et l'angle de déplacement θ est donné par la relation :

Nrev=θ/360°

La position verticale z de la plaque mobile peut être déduite à partir de θ en utilisant l'équation : z=Nrev *Deff * pi ⟹

z=θ/360° * Deff * pi

Ceci nous conduit aux expressions des modèles géométriques de translation axiale :

z=θ/360° * Deff * pi ( modele direct)
θ=(360°*z)/(Deff * pi ) ( modèle inverse)

Ces équations nous fournissent un moyen précis pour établir la position verticale de la plaque en se basant sur l'angle de rotation du servomoteur et, à l'inverse, pour calculer l'angle nécessaire pour atteindre une position verticale déterminée.

Etape 2 : conception CAO 🖥️✏️📐:

Nous passons maintenant à la phase de modélisation des composants de notre robot. Nous utiliserons SolidWorks pour cette tâche, un outil de CAO parfait pour transformer nos plans en modèles numériques. C'est une étape importante pour rendre nos idées concrètes et fonctionnelles.

Notre création robotique est une interprétation du robot pantographe, caractérisée par une conception où les axes de deux servomoteurs convergent, orchestrant les mouvements des bras et en conséquence, la trajectoire du stylo.

La structure du robot est articulée autour de trois sous-ensembles principaux:

Le bâti : Formant la fondation du robot, ce premier sous-ensemble est chargé d'accueillir et de stabiliser les deux servomoteurs principaux. Ces moteurs sont essentiels pour actionner les mouvements latéraux et longitudinaux, conférant au robot une capacité de translation précise sur le plan bidimensionnel.
Les Bras et le Porte-Stylo : Ce sous-ensemble représente les membres actifs du robot. Attachés aux servomoteurs, les bras articulés du robot sont la clé de sa capacité à dessiner. Ils suivent avec fidélité les instructions de mouvement pour guider le stylo sur la surface dédiée. ,
Le Mécanisme de Translation Verticale : Incorporant un système de pignon et crémaillère, ce troisième sous-ensemble enrichit le robot d'une fonctionnalité verticale. Il permet à la surface de dessin de s'élever ou de s'abaisser, donnant au robot la faculté de ponctuer le papier de dessins en pointillés ou de lever le stylo entre les points, conformément aux spécifications techniques préétablies.

figure 14 : Idée de bâti pour la modélisation

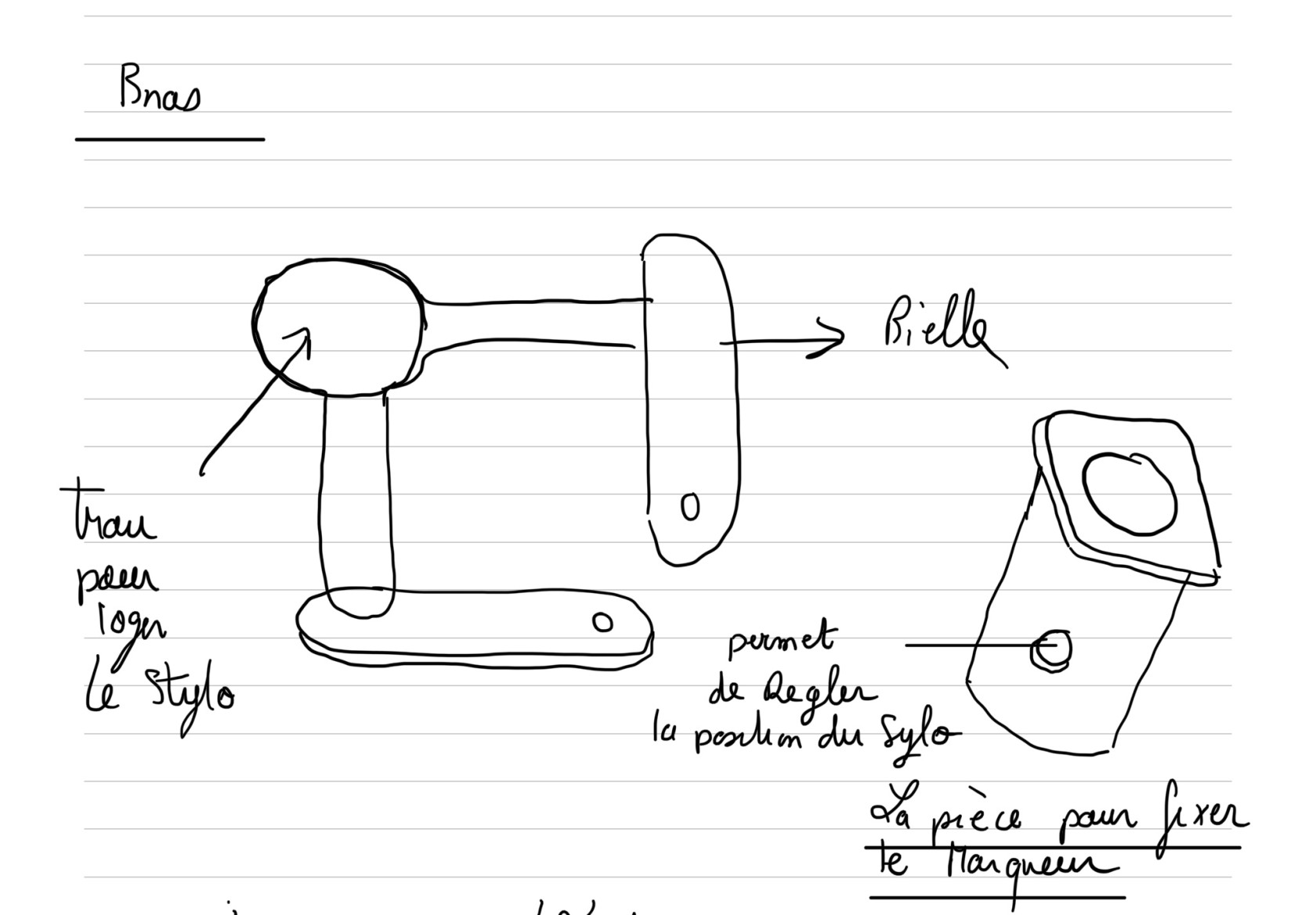
figure 15 : Idée de bras pour la modélisation

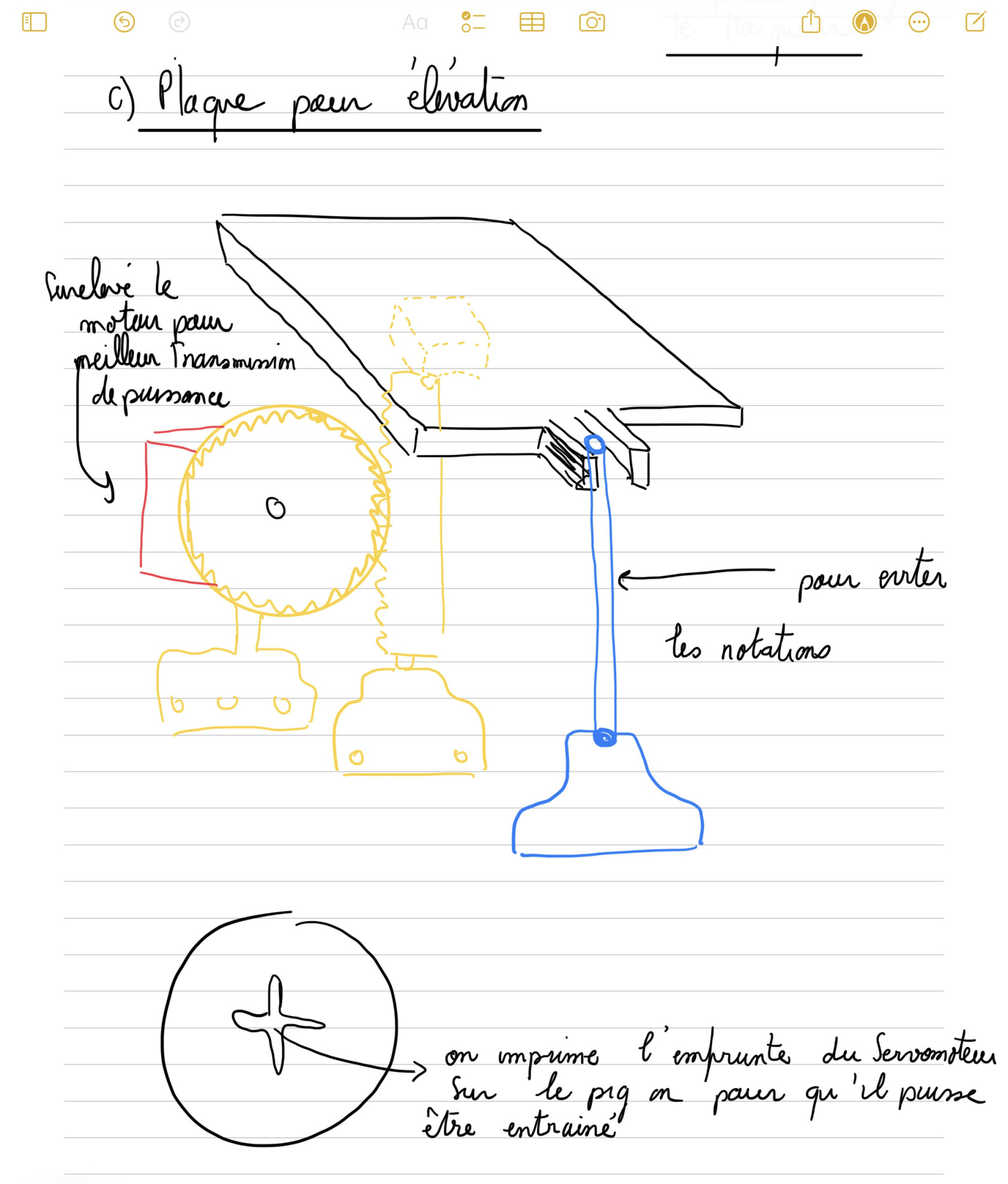
figure 16 : Idée de plaque élévatrice pour la modélisation

Pour garantir la stabilité de la plaque de dessin et éviter toute rotation indésirable, deux mesures ont été prises dans la conception :

Une liaison pivot a été établie entre la crémaillère et la plaque élévatrice. Cette liaison permet une translation verticale contrôlée tout en empêchant toute rotation autour de l'axe de déplacement.

Pour neutraliser toute rotation résiduelle, un point de contact ponctuel a été ajouté. Ce contact, illustré en bleu sur la figure 16, sert de contrainte supplémentaire qui limite le mouvement rotatif en imposant un seul point d'appui fixe sur la plaque

Journal de Bord - Évolution du Projet Robotique 🤖

07/02/2024:

Formation des Groupes : Les équipes ont été créées, favorisant une belle diversité de compétences et d'expériences.
Brainstorming : Séance intense de brainstorming en groupe. Des idées variées ont été proposées, allant de concepts innovants à des applications pratiques pour le robot.
Choix des Idées : Avec tant d'idées intéressantes, la difficulté principale était de se concentrer sur les plus réalisables. Trouver un consensus a pris du temps mais a été enrichissant. Heureusement, l'orientation des professeurs a été cruciale; ils nous ont guidés pour éviter de tomber dans des pièges ou de concevoir des prototypes irréalistes.
Planification Initiale : La mise en place d'un plan d'action initial a été un peu chaotique🚨, avec plusieurs opinions sur la direction à prendre. Après discussion, nous avons décidé de fusionner certaines idées pour créer un concept de robot plus cohérent et réalisable. Nous avons ainsi établi un plan d'action plus structuré pour la prochaine séance, en se concentrant sur des objectifs spécifiques.🚀

💡 Note pour la Prochaine Séance

Se concentrer sur l'élaboration d'un prototype de base pour le robot avec calculs précis des modèles cinématiques.
Affiner les rôles au sein de l'équipe pour une efficacité accrue.

21/02/2024:

🔧 Répartition des Tâches Aujourd'hui, nous avons réparti les tâches pour booster notre efficacité. Tandis qu’un travaillait sur la modélisation CAO sur SolidWorks, les autres se sont concentrés sur le modèle électronique pour Arduino et la création du code informatique pour assurer les mouvements adéquats du robot.

Électronique et Informatique
- La partie électronique-informatique est maintenant réalisée et fonctionnelle. Un grand pas en avant pour notre projet !
Réflexion sur la Création des Pièces
- Nous avons décidé des matériaux à utiliser et de l'épaisseur souhaitée pour nos pièces.
- Les mesures clés, comme la longueur des bielles formant le bras et du bâti, ont été déterminées.
- Première expérience avec la machine à découpe laser. Nous avons identifié certaines contraintes : principalement, le laser est plus adapté pour graver que pour faire de gros trous, pour éviter d'enflammer le matériau.
- Nos pièces seront conçues pour s'emboîter, à la manière des petites boîtes à idées du FabLab, avec des encoches pour faciliter la fixation.
Retour sur le Modèle Géométrique
- Moment de discussion enrichissant avec le professeur à propos de nos calculs géométriques. Cette révision nous a permis d'affiner notre approche.

🔜 Prochaines Étapes

- Notre objectif pour la prochaine séance est d'avoir terminé la modélisation afin de la soumettre aux professeurs pour validation.
- Nous envisageons de commencer la fabrication des pièces avec la découpe laser.