Stick-Slip
Information
- Contacts : Benjamin MARTINEZ & Nathan THORPE (benjamin.martinez@etu.sorbonne-universite.fr et nathan.thorpe@etu.sorbonne-universite.fr )
- Etudes : L3 Majeurs Sciences de la Vie mineurs Sciences de la Terre
- Dates du projet : 24 Janvier - 23 Mai 2025
- Responsables de l'UE LU3ST062 : Loïc LABROUSSE et Pierre THERY
- Responsable Projet Stick-Slip : Loïc LABROUSSE
Présentation du sujet :
Explication du Projet : Modélisation de la réaction de la croûte terrestre suite à la formation d'une faille à partir d'un modèle comportant un tapis roulant sur lequel sont placés de tampons (ou patins) retenus par des ressorts tels que :
Ce modèle s'appuie sur le livre "La déformation des roches" écrit par Mr. LABROUSSE et Mr. YAMATO, et plus précisément sur la partie 5, au chapitre 17 : la dynamique du glissement co-sismique; 1.1 Le modèle du patin ressort.
Cahier des charges :
Pour réaliser ce projet, nous avions plusieurs demandes :
- Tout d'abords, reprendre le modèle en LEGO à un seul tampon déjà existant, comprendre son fonctionnement, et identifier ses points forts et ses points faibles
- Trouver et utiliser une courroie adaptée comme tapis roulant, idéalement dentée (les dents permettant de mieux récupérer l'énergie mécanique transmise par le moteur via un système d'engrenages)
- Créer un cadre solide pour rigidifier et consolider la structure et éviter que les tampons ne quitte la courroie.
- Trouver un moyen de limiter les frottements des tampons avec le cadre
- Modifier la structure des tampons pour y placer un téléphone dessus et réaliser des mesures
- Conceptualiser un programme Python capable de récupérer les données via Phyphox
Contraintes et difficultés rencontrées :
- Trouver une courroie peu chère aux dimensions souhaitées
- L'acquisition de données réalisée par Phyphox présente une erreur systématique. En effet, le logiciel considére une accélération constante, peu importe sa valeur, indiquant une vitesse croissance et donc un déplacement constant, même alors que le téléphone est immobile. Il est donc nécessaire de corriger cette erreur au sein de notre code afin d'avoir des données justes.
- Trouver des ressorts avec une constante de rappel K suffisamment grande pour tirer le patin lors des pertes d'adhérences sur le support mais également suffisamment faible pour permettre une certaine liberté de mouvement
- Trouver un moyen de rendre le patin adhérent à la courroie pour créer une différence importante entre l'énergie nécessaire pour le mettre en mouvement et l'énergie nécessaire pour le maintenir en mouvement (c'est-à-dire le ramener alors que la pièce à commencer à bouger)
Montage:
Calculs et codes :
Code Python pour acquisition de données
import numpy as np
import matplotlib.pyplot as plt
import os
from io import StringIO # Permet de manipuler les données après conversion
def integ_acc(acc, dt):
"""Intégration de l'accélération pour obtenir la vitesse et la position."""
V = np.zeros(len(acc))
P = np.zeros(len(acc))
v, p = 0, 0
for i, a in enumerate(acc[1:], start=1):
dv = a * dt
v += dv
dp = v * dt
p += dp
V[i] = v
P[i] = p
return V, P
def corr_acc(acc, temps, n):
"""Correction de la dérive des données d'accélération."""
fit = np.polyfit(temps, acc, n)
acc_corr = acc - np.polyval(fit, temps)
return acc_corr
# Définition du chemin du fichier CSV
filename = r'C:\Users\21205260\Desktop\Data from phyphox\Raw Data.csv'
# Vérifier si le fichier existe avant de le charger
if not os.path.isfile(filename):
print(f"❌ Fichier introuvable : {filename}")
exit()
else:
print(f"✅ Fichier trouvé : {filename}")
# Chargement sécurisé des données avec conversion des `,` en `.`
try:
with open(filename, 'r', encoding='utf-8') as f:
raw_data = f.read().replace(',', '.') # Convertir les séparateurs décimaux
# Création d'un buffer pour lire les données converties
data_buffer = StringIO(raw_data)
# Chargement des données avec le bon séparateur `;`
donnees = np.genfromtxt(data_buffer, delimiter=';', skip_header=1, dtype=float)
# Vérification que des données ont bien été chargées
if donnees.size == 0:
print("⚠️ Erreur : Le fichier est vide ou mal formaté.")
exit()
# Suppression des lignes contenant NaN
if np.isnan(donnees).any():
print("⚠️ Attention : Certaines valeurs sont NaN, elles seront ignorées.")
donnees = donnees[~np.isnan(donnees).any(axis=1)]
except Exception as e:
print(f"❌ Erreur lors du chargement du fichier : {e}")
exit()
# Extraction des valeurs de temps et accélération
temps = donnees[:, 0]
# Vérifier que `temps` contient bien des valeurs avant de calculer `dt`
if temps.size < 2:
print("⚠️ Erreur : Pas assez de valeurs dans `temps` pour calculer `dt`.")
exit()
dt = temps[1] - temps[0]
accX = donnees[:, 1]
accY = donnees[:, 2]
accZ = donnees[:, 3]
# Aperçu des données corrigées
print("📊 Aperçu des premières valeurs du temps :", temps[:5])
print("📊 Aperçu des premières valeurs d'accélération X :", accX[:5])
# Correction de la dérive
n = 1
aX_c = corr_acc(accX, temps, n)
aY_c = corr_acc(accY, temps, n)
aZ_c = corr_acc(accZ, temps, n)
# Intégration des données
[vX, pX] = integ_acc(accX, dt)
[vX_c, pX_c] = integ_acc(aX_c, dt)
[vY, pY] = integ_acc(accY, dt)
[vY_c, pY_c] = integ_acc(aY_c, dt)
[vZ, pZ] = integ_acc(accZ, dt)
[vZ_c, pZ_c] = integ_acc(aZ_c, dt)
# Affichage des graphiques
fig, axs = plt.subplots(3, figsize=(8, 10))
axs[0].plot(temps, accX, label="Accélération X")
axs[1].plot(temps, accY, label="Accélération Y")
axs[2].plot(temps, accZ, label="Accélération Z")
for ax in axs:
ax.legend()
plt.show()
fig1, ax1 = plt.subplots(3)
ax1[0].plot(temps, accX, 'b', label="Brut")
ax1[0].plot(temps, aX_c, 'r', label="Corrigé")
ax1[1].plot(temps, vX, 'b', label="Vitesse brute")
ax1[1].plot(temps, vX_c, 'r', label="Vitesse corrigée")
ax1[2].plot(temps, pX, 'b', label="Position brute")
ax1[2].plot(temps, pX_c, 'r', label="Position corrigée")
for ax in ax1:
ax.legend()
plt.show()
fig4, ax4 = plt.subplots()
ax4.plot(pX, pY, 'b', label="Trajectoire brute")
ax4.plot(pX_c, pY_c, 'r', label="Trajectoire corrigée")
ax4.legend()
plt.show()
Code Patin
largeur=9;
longueur=6.5;
hauteur=2;
difference(){
cube(size = [largeur,longueur,hauteur], center = false);
translate([largeur/3,-0.1,hauteur/3])cube (size = [largeur/3,longueur/5,hauteur]);rotate(a=[0,115,0]) translate([-1,-0.01,-1.5])cube (size = [3,longueur+1,10]);rotate(a=[0,-115,0]) translate([-5.8,-0.01,-13])cube (size = [3,longueur+1,10]);translate([largeur/16,longueur/4,hauteur-3])cylinder(h=4, d=0.8,$fn=30, center=false);translate([largeur/16,longueur/1.2,hauteur-3])cylinder(h=4, d=0.8,$fn=30, center=false); translate([largeur/1.06,longueur/1.2,hauteur-3])cylinder(h=4, d=0.8,$fn=30, center=false); translate([largeur/1.06,longueur/4,hauteur-3])cylinder(h=4, d=0.8,$fn=30, center=false);
}
union (){
translate([largeur/6,0.35,hauteur-0.4])rotate(a=[0,90,0])cylinder(h=largeur/1.5, d=0.65,$fn=30, center=false); translate([largeur/2,longueur/2,hauteur-0.4])cylinder(h=1.2, d=0.65,$fn=30, center=false);translate([(largeur/2)+0.1,0.35,hauteur-0.4])rotate(a=[0,90,0])cylinder(h=0.1, d=0.9,$fn=30, center=false);translate([(largeur/2)-0.2,0.35,hauteur-0.4])rotate(a=[0,90,0])cylinder(h=0.1, d=0.9,$fn=30, center=false);
}
Code Axe moteur
Code Axe Tension de la courroie
Code Axe soutien
Fichiers STL et Aperçus 3D
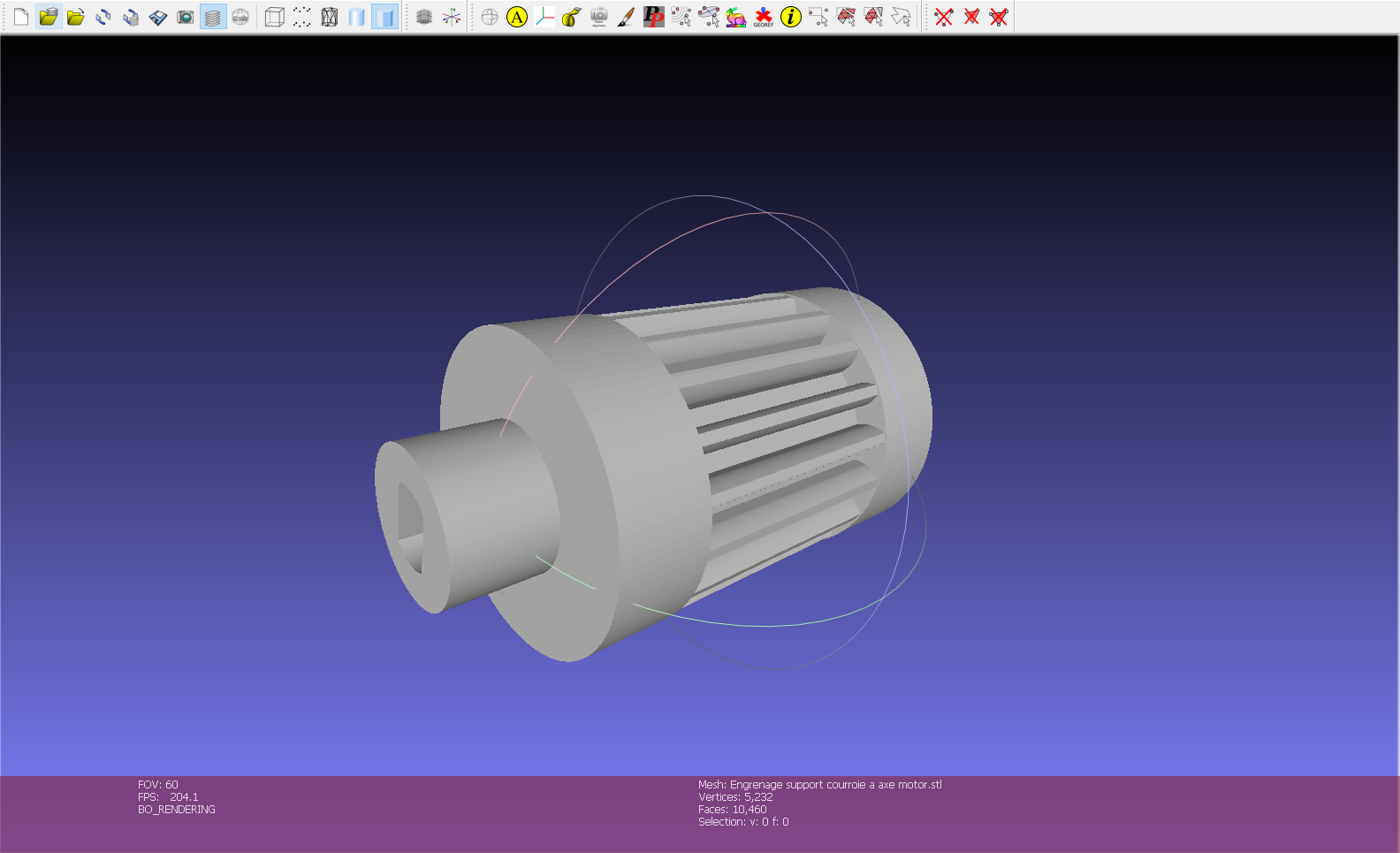
Engrenage support courroie a axe motor.stl
Engrenage support courroie b.stl
1.Montage:
- Choix des matériaux et pièces structurales. On utilisera deux planches de contreplaqué en bois de 2cm d'épaisseur pour 1m de longueur comme paroies latérales, un moteur DC de 30 Volts, et une courroie crantée d'un pas de 8mm et d'une longueur totale de 1m58.
- Les planches coupées et les pièces en notre disposition, les planches sont ensuite percées pour obtenir une fente de glissement nécessaire à l'axe de tension et des trous accueillant les morceaux de barres de métal de 10 cm pour les axes centraux de soutien. Un carré est découpé pour accueillir le moteur. Afin de rigidifier la structure des pièces en bois auxiliaires sont fixées en pontage entre les deux planches.
- Une fois les axes crantés imprimés en 3D, ils sont fixés respectivement au moteur, aux petites barres de soutien transversales de la courroie, et dans les fentes de glissement avec deux vis de compression ajustables, des roulements à billes et des chutes de bois.
- La courroie est placée sur les axes et le patin imprimé est muni de roulements à billes servant de roues latérales, de textile FFP2 sur la face inférieure pour le contrôle du frottement avec la courroie, d'un fixateur de téléphone pour stick de selfie et d'un ressors relié à une vis sur une extrémité du stick slip. Le moteur est relié à un contrôleur de puissance pour ajuster la vitesse des axes.
- Le montage prêt, on lance le moteur et collecte des mesures en temps réel sur Phyphox installé préalablement sur le téléphone test.
2.
3.
4.
5.
Résultats :
Données test
Graphiques
Ces résultats présentent les acquisitions pour un seul patin, avec donc un seul téléphone. La courbe décrivant les mouvements de stick-slip est celle décrivant l'accélération y.
Nous pouvons constater plusieurs choses. La première est que les pics décrivent les moments où l'adhérence est perdue (passage de stick à slip). Il ne semble pas y avoir de pattern à cela, semblant indiquer des mouvements chaotiques comme décrit dans le livre de Mr.LABROUSSE et Mr.YAMATO. La seconde est qu'il n'y a pas de grandes différences d'intensité entre les pics et le reste de la courbe, indiquant que le patin n'avait pas un mouvement fluide et qu'il réalisait beaucoup de stick-slip sur de faibles distances.
Conclusion et ouverture :
Selon nous, le modèle que nous avons réalisé réponds aux différentes demandes du cahier des charges. Tout d'abord, il s'agit d'une version plus grande du modèle déjà existant en LEGO, avec une prise en compte des défauts de ce modèle lors de la conception du notre pour éviter de les reproduire. Ensuite, nous avons un modèle solide, facilement modulable si besoin, avec une courroie dentée permettant un bon transfert d'énergie entre le moteur et celle-ci à l'aide d'engrenage. Nous avons modifiés les patins afin de pouvoir y fixer un téléphone ainsi que des poids si nécessaires. Nous avons également résolu le problème de frottements contre le cadre à l'aide des roulements à billes placés sur le patin. Enfin, nous avons un programme Python capable de réceptionner les données émises par Phyphox et de les retranscrire sous forme de graphiques. Cependant, bien que notre modèle soit fonctionnel, il nécessite des ajustements pour fournir des résultats clairs et exploitables avec plusieurs téléphones. Tout d'abord, il faudrait trouver une solution pour accroitre l'adhérence des patins sur la courroie (tester différents matériaux à placer sur la base du patin), permettant ainsi de réduire les mouvements saccadés du patin. Ensuite, il nous faut trouver un moyen de maintenir les patins en place pour éviter qu'ils se retrouvent catapulté lorsqu'ils sont attachés en chaine (peut-être en mettant en place un système de rail). Enfin, nous avons rencontrés des difficultés à trouver des ressorts de tractions adaptés, ainsi peut-être faudrait-il tester avec des ressorts avec une force de rappel différentes ou bien avec des ressorts. Enfin, peut-être investir dans d'autres types de courroies pour faire varier l'adhérence du support et peut-être observer des variations notables du comportement des patins.
Remerciements :
Nous aimerions remercier Loïc LABROUSSE et Pierre THERY pour toute leur aide sur le projet, que ça soit dans le montage comme dans la programmation. Nous voudrions également remercier Christian SIMON et les fabmanagers pour leur aide bienveillante au prototypage. Finalement, nous aimerions remercier Victor BRIOT pour son aide concernant nos difficultés de programmation et soucis liés au matériel informatique.
Journal de Bord
24/01/2025
Explication du Projet : Modélisation de la réaction de la croûte terrestre suite à la formation d'une faille à partir d'un modèle comportant un tapis roulant sur lequel sont placés de tampons (ou patins) retenus par des ressorts tels que :
Idées :
- Reprendre le modèle en LEGO à un seul tampon déjà existant (comprendre son fonctionnement, identifier ses points forts et ses points faibles)
- Utiliser une courroie de vélo sans chaine comme tapis roulant (les dents permettant de mieux récupérer l'énergie mécanique transmise par le moteur via un système d'engrenages)
- Créer un cadre en bois pour solidifier la structure et éviter que les tampons ne quitte la courroie (utiliser du bois de type contreplaqué 7 plis)
- Créer un système de rail en aluminium afin de limiter des frottements des tampons avec le cadre (utiliser des roues avec roulements à billes dans les rails)
- Modifier la structure des tampons pour y placer un téléphone dessus et réaliser des mesures
- Conceptualiser un programme Python capable de récupérer les données via Phyphox
Livre sur le sujet :
La déformation des roches - LABROUSSE et YAMATO (partie 5, chap.17 : la dynamique du glissement co-sismique; 1.1 Le modèle du patin ressort)
31/01/2025
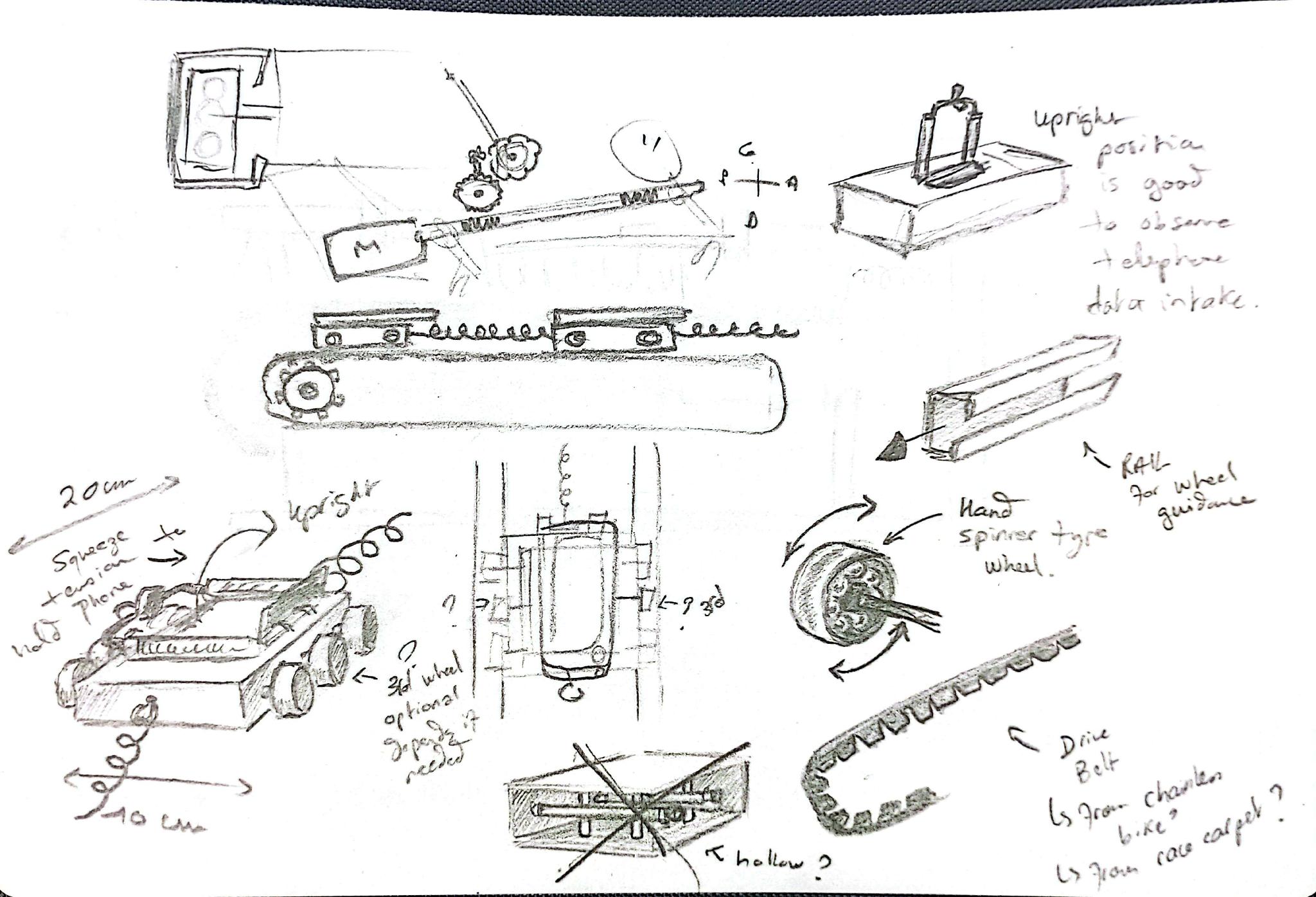
- Conceptualisation rapide de l'ensemble du modèle avec un focus sur les patins
- Etablir la liste des matériaux et parties utiles à la conception
- Début de schématisation graphique du prototype de patins
Fig 1: Brouillon , Brainstorming sur le design des patins avec porte-téléphone et modèle du rail.
07/02/2025
- Recherches sur les modèles de courroie potentiels:
I. BELTSERVICE CORPORATION (page d'accueil site officiel)
BROCHURE
Avantages
- Produits vendus au mètre
- Multiples Choix de matériaux et formes
- Qualité professionnelle
Inconvénients
- Fournisseur à l'étranger, potentiels frais d'importation
- Fournisseur industriel, prix industriel peut-être pas avantageux
- Demandent beaucoup d'informations et de prise de contact, n'offrent pas directement les produits avec les prix
Conclusion: Mauvais choix
II. RS-ONLINE
Courroie Contitech CONTI FO-Z, Section XPZ, long primitive : 1950mm, long int: 1874mm, long ext : 1963mm
https://fr.rs-online.com/web/p/courroies-en-v-et-courroies-trapezoidales/4742613?gb=s
Avantages
- 1963 mm -> longueur satisfaisante pour le projet
- Prix abordable
- Bonne disponibilité
- Engrenage adapté disponible
Inconvénients
- Largeur de la bande insuffisante -> plusieurs seront nécessaires (2 ou 3)
Conclusion: Bon choix
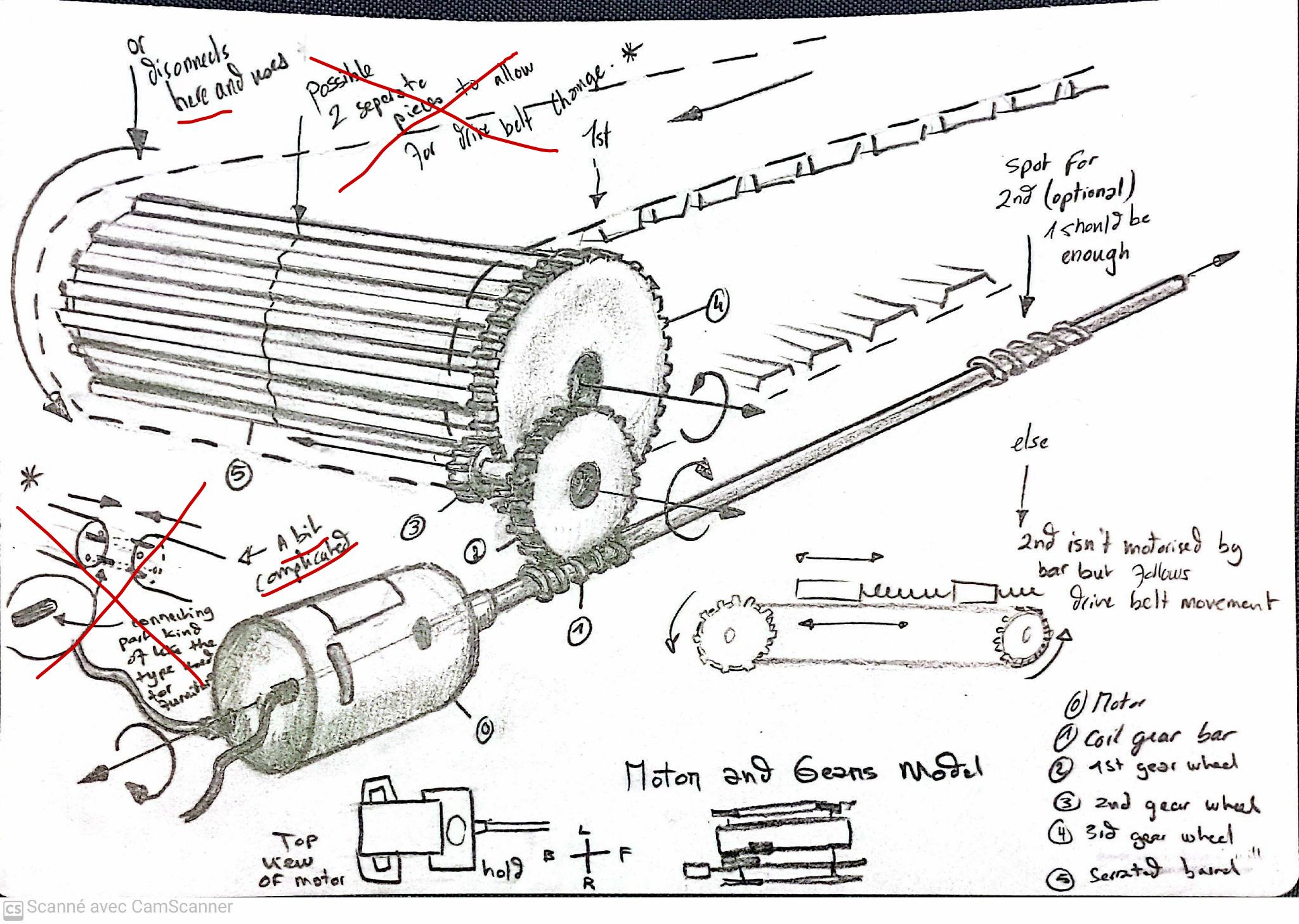
- Schématisation de la motorisation et des engrenages (repris du modèle des années précédentes)
Fig 2: Brainstorming , Schématisation de la motorisation et des engrenages avec quelques théories sur comment démonter facilement pour éventuellement pouvoir changer la courroie.
15/02/2025
REMARQUE: Nous sommes trop lents sur le théorique, il faut faire avancer la partie pratique.
- Recherche dans les réserves du fablab pour des roulements à billes
-
Basé sur les données géométriques de la courroie nous estimons avoir besoin de parois latérales d'au moins:
1m de longueur, 10 cm de largeur , 3 cm d'épaisseur.
- Pour estimer la tailles des trous de l'axe à percer sur les parois, il faut savoir quel moteur utiliser: Nous sommes allés au fablab voir quels moteurs étaient disponibles: Nous avons été conseillé des moteurs plus puissants pour notre projet (moteurs pas à pas), nous avons aussi testé la puissance du moteur déjà présent sur le modèle LEGO -> selon les aides du fablab il devrait être déjà suffisamment puissant.
- Recherche de code pour le transfert du data de phyphox en temps réel: https://github.com/frederic-bouquet/phyphox-dataviz-tools
20/02/2025
Inventaire des rails alluminium en stock et autres matéiaux disponibles: rails grands et moyens, peut-être un peu grands , roulements à billes n'ont pas d'axes donc il faudrait en rajouter un.
Découpe des côtés structuraux en contreplaqué à la menuiserie du fablab, puis ponçage à la machine et à la main.
Dimensions: 100x10x2 cm
 Fig 3: Étapes et matériel de la découpe et du ponçage des parois structurales en contreplaqué du Stick-Slip
Fig 3: Étapes et matériel de la découpe et du ponçage des parois structurales en contreplaqué du Stick-Slip
Les fabmanagers n'étant pas présents, l'utilisation de scie sauteuse n'était pas autorisée, la découpe a donc été faite avec une scie manuelle (travail plus long), la scie circulaire n'étant pas adaptée pour la longueur de découpe. En conséquent seule une des deux parois est coupée et ponçée l'autre est à moitié coupée. Les deux sont stockées au fablab prototypage.
Prochaine étape: Prototypage est fermé le Vendredi 21/02/2025, ce jour là nous avancerons sur le modèle 3D du patin et un cylindre test.
21/02/2025
Découpe de la deuxième planche à la scie sauteuse et ponçage (finalement on a eu accès à prototypage). Découpe d'axes cylindriques tests en bois pour tester un assemblage avec le moteur et engrenages.
21/02/2025
- Découpe de la deuxième planche à la scie sauteuse et ponçage (finalement on a eu accès à prototypage).
- Découpe d'axes cylindriques tests en bois pour tester un assemblage avec le moteur et engrenages.
- Recherches sur le programme pour collecter en temps réel les données de phyphox.
Fig 4: Planches de bois et axes cylindriques avec chutes pour le test moteur
03/03/2025
- Recherche d'une nouvelle courroie : modèle envisageable -> https://allocourroies.com/courroie-simple-dentee-htd/7732-courroie-simple-dentee-1000h-100.html
07/03/2025
- Nouvelle courroie , modèle choisi : https://allocourroies.com/
courroie-trapezoidale-lisse/ 3994-courroie-trapezoidale- lisse-c77.html - Model test sur lego de patin:
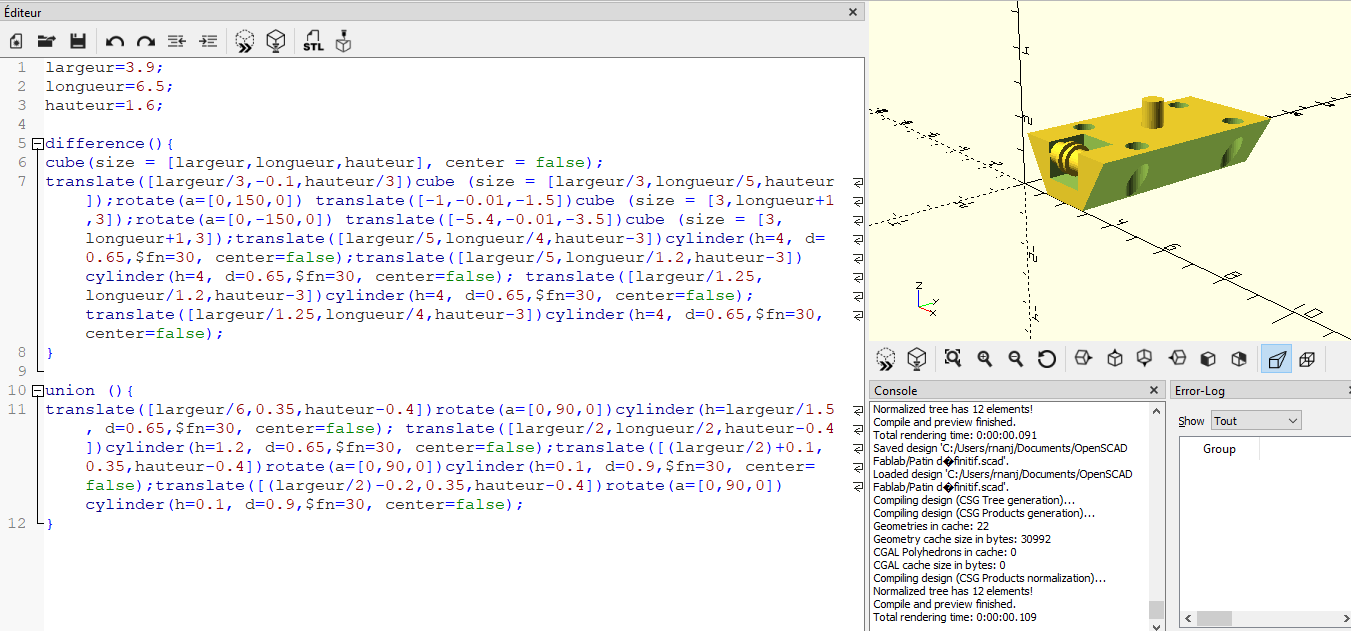
1. Design
Fig 5: Modèle 3D et programme OpenScad du patin 1.0
2. Impression
Fig 6: Impression 3D du patin test
3. Test
Fig 7: Installation pour le test du patin avec PhyPhox
- Test du prototype fig 7:
- Résultats: Problème de force de rappel insuffisante, problème de trainée de la courroie par les axes...
PHYPHOX
Mr. LABROUSSE est venu nous prêter main forte avec le programme permettant de transmettre les données de Phyphox vers un programme Python, nous permettant ainsi de collecter les données. Nous avons rencontré certains soucis, liés à une erreur systématique de Phyphox, qui considérait qu'une accélération constante, peu importe sa valeur, indiquait une vitesse croissance et donc un déplacement constant, même alors que le téléphone était immobile
14/03/2025
Mr. LABROUSSE est revenu avec un nouveau programme, corrigeant globalement l'erreur systématique de Phyphox. Nous avons essayé de le tester en situation réelle, en utilisant les premières versions déjà existante en LEGO du Stick-slip, cependant nous avons rencontré de nombreuses difficultés : des problèmes d'adhérences du programme, le cadre du stick-slip qui a cédé à quelques endroits, la nécessité de rallonger la structure, un changement de ressort avec une constante de rappel k adaptée, ainsi que la chaine d'engrenage alimentant la bande qui avait du jeu et qui a fini par ne plus fonctionner après une dizaine de secondes d'utilisation (à cause de la vitesse de rotation importante, amenant certaines pièces à fondre).
Après avoir remanié la longueur du stick-slip et placé un œillet pour limiter les frottements entre les différentes pièces, et donc la fonte, une somme parvenu à faire fonctionner notre stick-slip de manière plus durable. En revanche, nous ne sommes pas parvenu à réaliser les tests voulu avec notre téléphone placé sur le patin, la force de rappel des patins n'étant pas assez puissante.
Nous avons décider de changer de nouveau de courroie, afin d'en avoir une dentée. Nous avons donc prise celle-ci : https://allocourroies.com/courroie-simple-dentee-htd/7236-courroie-simple-dentee-2000-8mhtd20.html-en-v-et-courroies-trapezoidales/4742613?gb=s
21/03/2025
Après avoir remanié la longueur du stick-slip et placé un œillet pour limiter les frottements entre les différentes pièces, et donc la fonte, une somme parvenu à faire fonctionner notre stick-slip.
Aujourd'hui, nous avons décidés de retirer le moteur du prototype de stick-slip et d'installer une manivelle à la place, afin de pouvoir tester en conditions réelles le programme que nous a fourni. Après avoir modifié de nouveau la structure, nous sommes arrivés à ceci :
Fig 8: Installation pour le test du patin avec PhyPhox avec manivelle manuelle.
Nous aurions besoin de ressorts avec une force de rappel plus importante, car pour le moment, ceux que nous avons ramène difficilement le patin lorsque un téléphone est placé dessus.
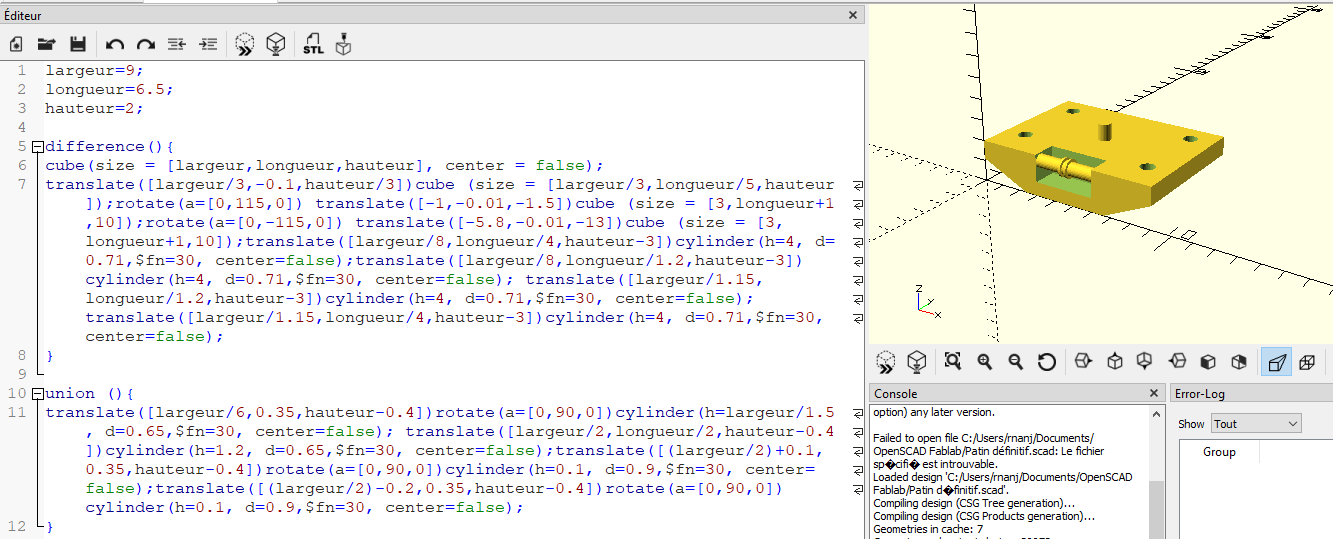
Nous avons également modélisés en 3D la structure du patin qui sera utilisé pour notre construction finale. nous allons reprendre des éléments créés lors d'un projet précédent (le projet riedle : https://wiki.fablab.sorbonne-universite.fr/wiki/doku.php?id=wiki:projet:riedel), afin de bloquer nos roulements à billes sur notre patin à l'aide de tiges qu'ils ont modélisé. Nous arrivons donc à cette structure :
Fig 9: Modèle 3D et programme OpenScad du patin 1.1
28/03/2025
Fig 10: Brainstorming avec moteur potentiel à pas (nous doutons que ce soit le plus judicieux) et axe tests en bois
Fig 11: Modèle 3D et programme OpenScad du patin 1.2
Nous avons encore changé de courroie, puisque celle que nous avions reçu avait un revêtement plastique et non en caoutchouc.
04/04/2025
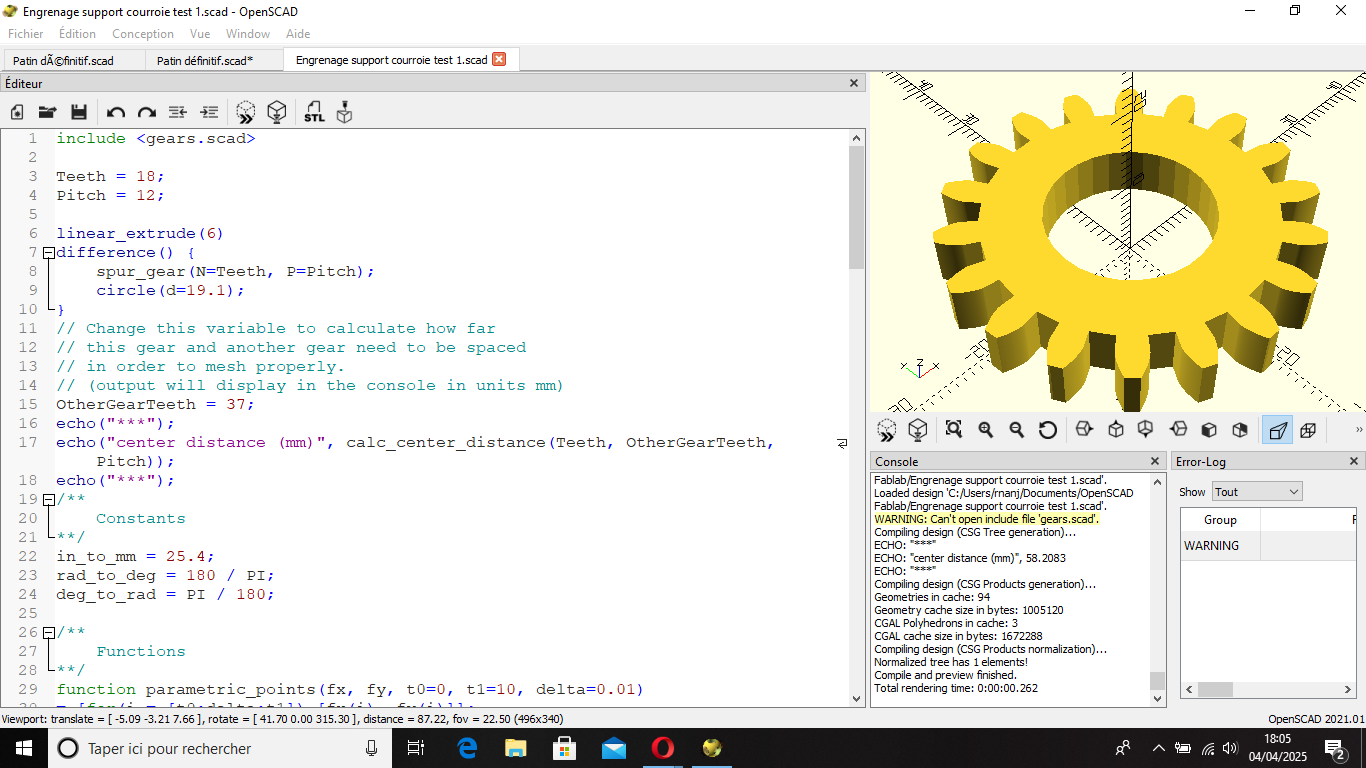
Nous avons commencé à modéliser des engrenages pour le projet
Fig 12: Modèle 3D et programme OpenScad de l'axe de l'engrenage courroie 1.0
11/04/2025
Nous avons reçu la courroie finale et le moteur DC final pour le montage:
Fig 13: Courroie et moteur DC finaux
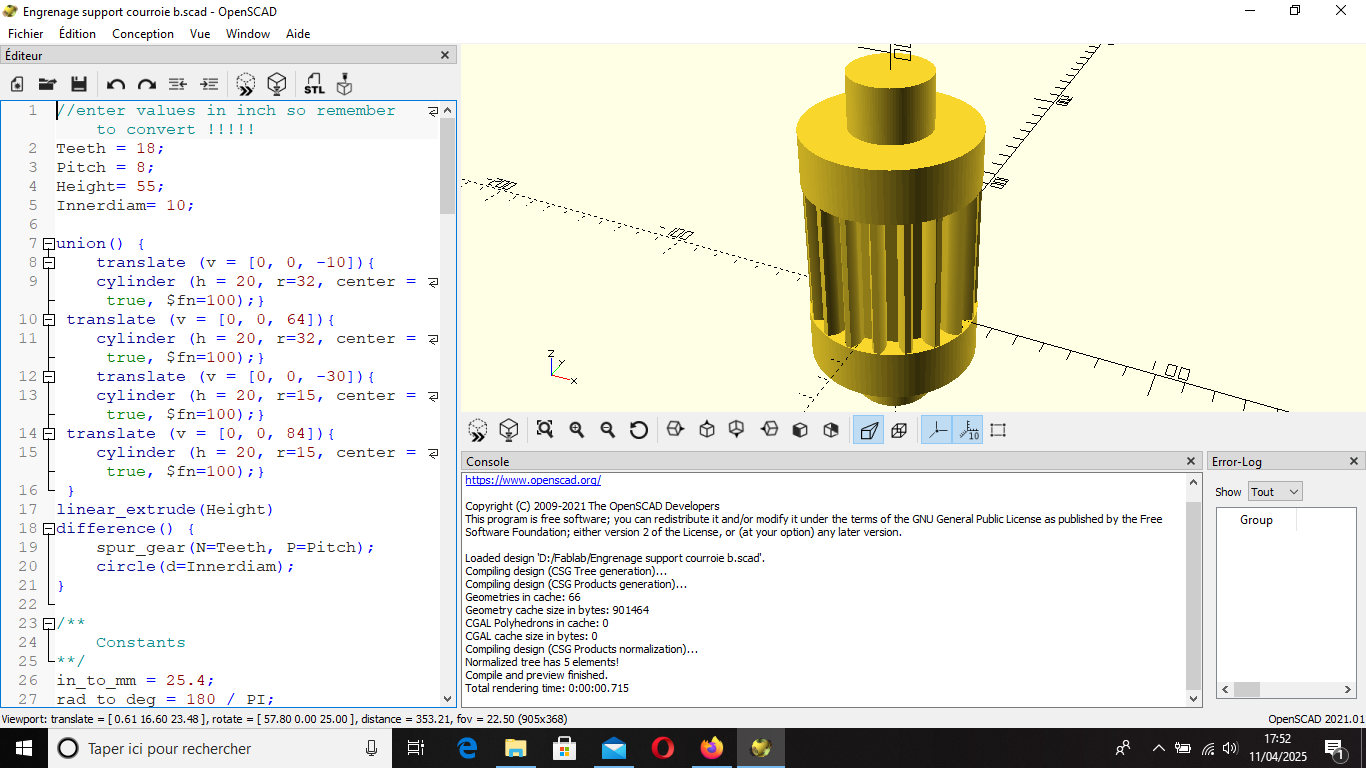
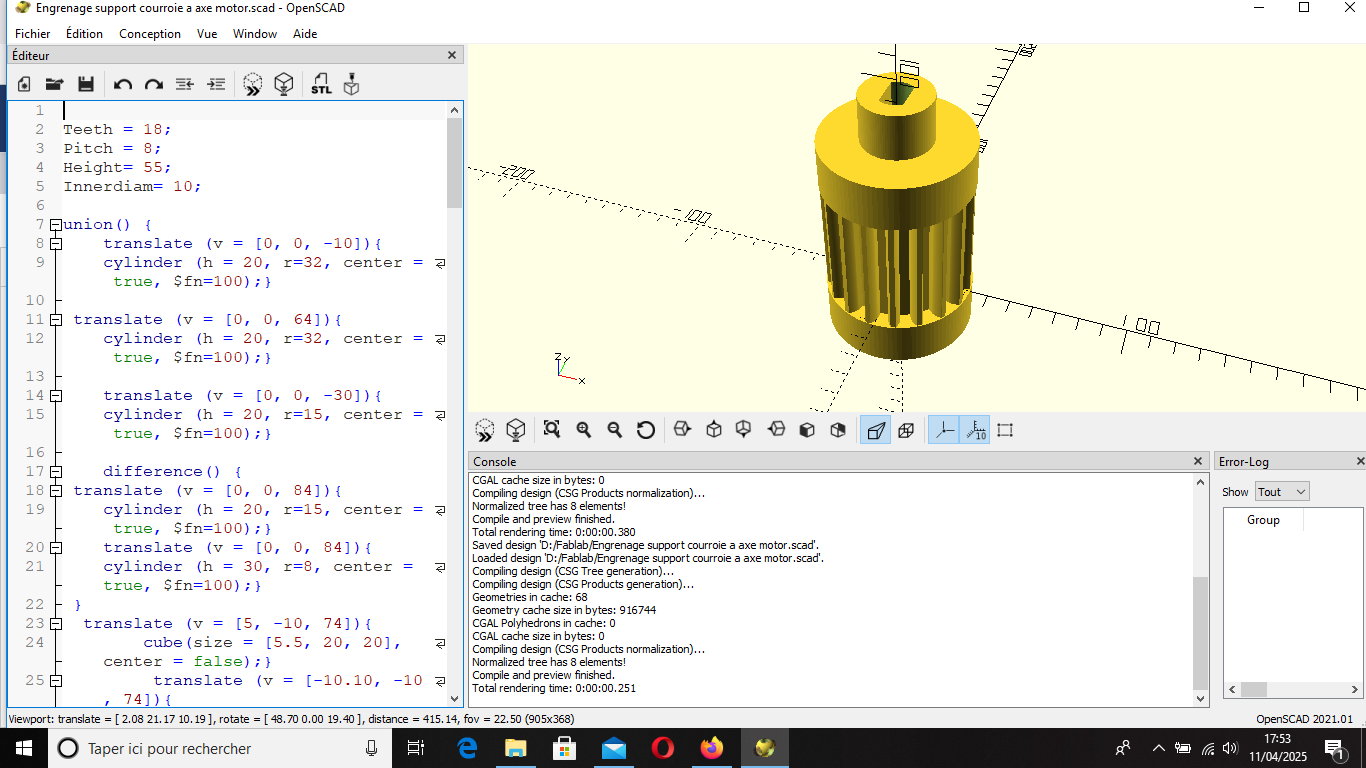
Nous avons aussi réalisé les axes d'entrainement de la courroie a et b en utilisant les paramètres de celle-ci en 3D sur Openscad: 1800, 8M
Fig 14: Brainstorming pour le code OpenScad du patin 1.1
Fig 15: Modèle 3D et programme OpenScad de l'axe de l'engrenage courroie b 1.1
Fig 16: Modèle 3D et programme OpenScad de l'axe de l'engrenage courroie a 1.1
Nous avons également discuté d'élaborer un système permettant de maîtriser la tension de la courroie sur le projet et de pouvoir modifier facilement le poids du patin si nécessaire.
PROCHAINES ETAPES:
- Trouver des ressors adaptés
- Imprimer les axes
- Finir de monter le système motorisé sur la courroie
- Mettre au point un système de maintien de la courroie pour la portion plateau de glissage
- Finir les modifications du patin pour le placement des roues de guidage
18/04/2025
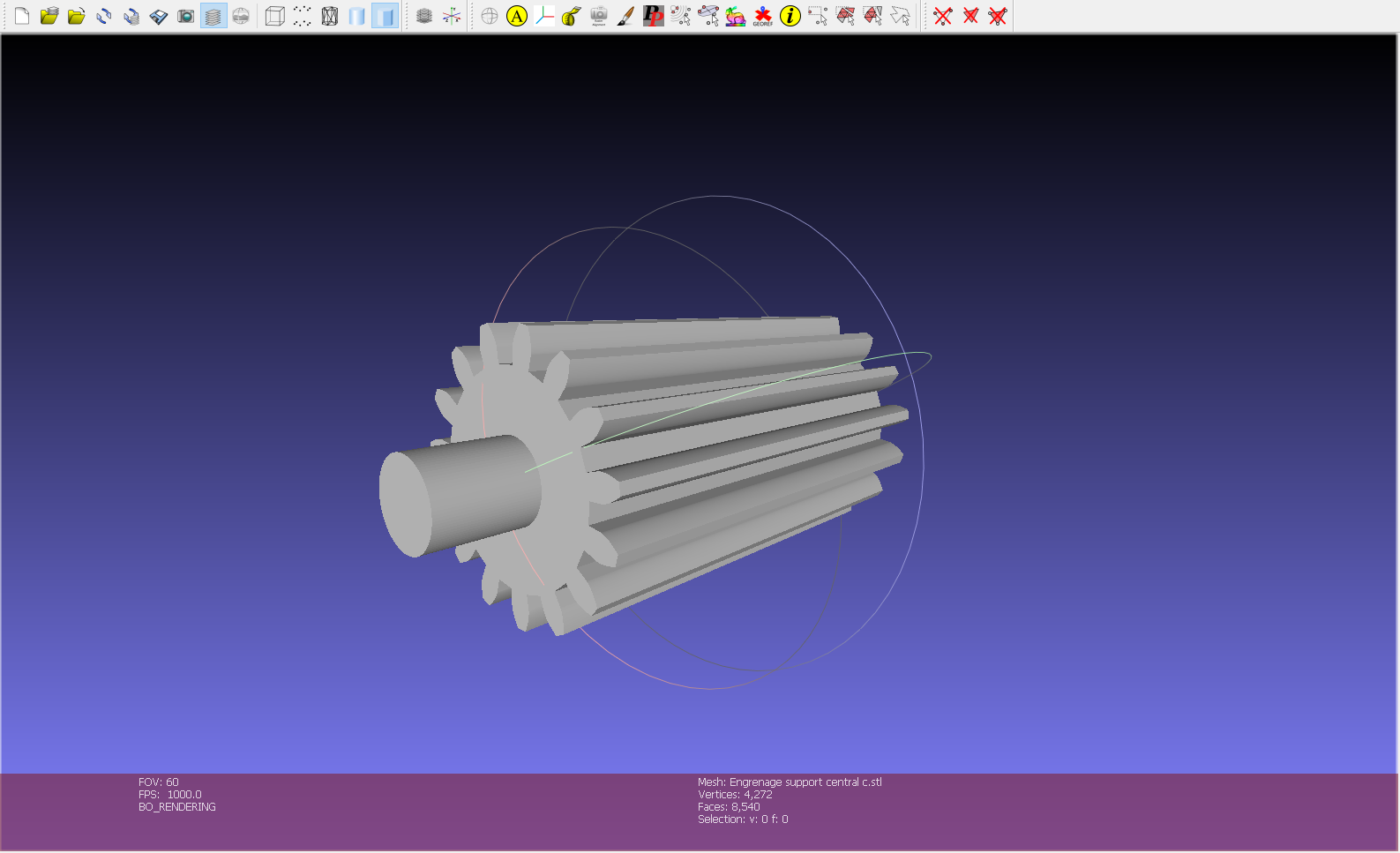
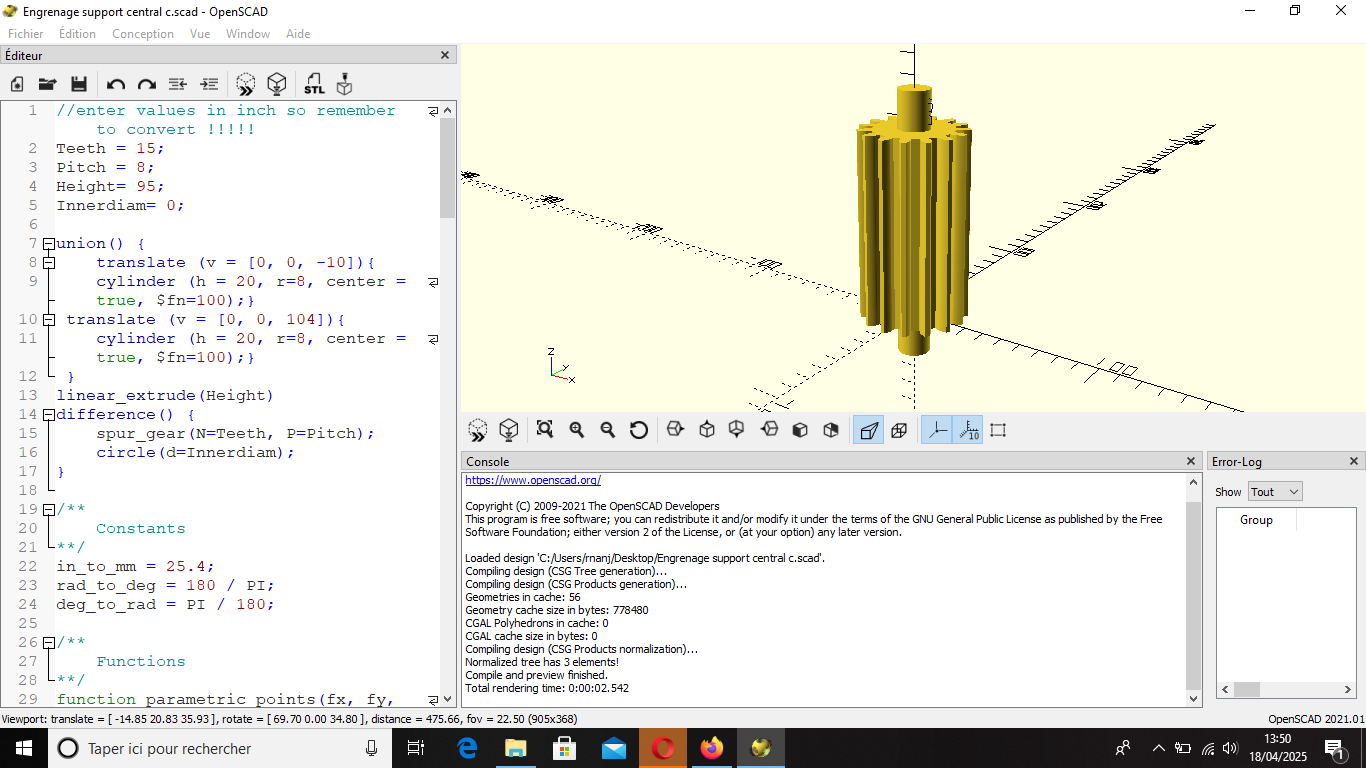
Fig 17: Modèle 3D et programme OpenScad de l'axe des engrenages support central courroie c 1.1
02/05/2025
Début du montage à partir des axes améliorés par Pierre Thery.
Nous avons percé les planches pour créer une fente de glissement pour l'axe permettant de tendre la courroie et un trou pour fixer le moteur.
Lors du montage la découpe d'un emplacement pour le moteur sur les planches les a fragilisés et une section s'est cassé
Suite : Réparations nécessaires + construire système pour l'axe
09/05/2025
Réparations effectués, merci à Pierre pour l'aide.
Le montage permet un axe amovible afin de tendre la courroie, nous avons percé de multiples trous pour placer les axes de soutien de la courroie.
Fig 18: Montage de l'axe amovible de tension de la courroie
Fig 19: Montage des axes de soutien de la courroie.
16/05/2025
Après avoir testé plusieurs matériaux et ressors pour trouver le rapport adhérence/glissement optimal du patin nous avons choisis le matériau textile de filtre FFP2 comme base sur la face inférieure du patin. Nous avons pu ensuite collecter un jeu de données test pour élaborer des graphiques avec une version révisée du code python de traitement des données.
Modèles :