Retour sur la vitesse en X

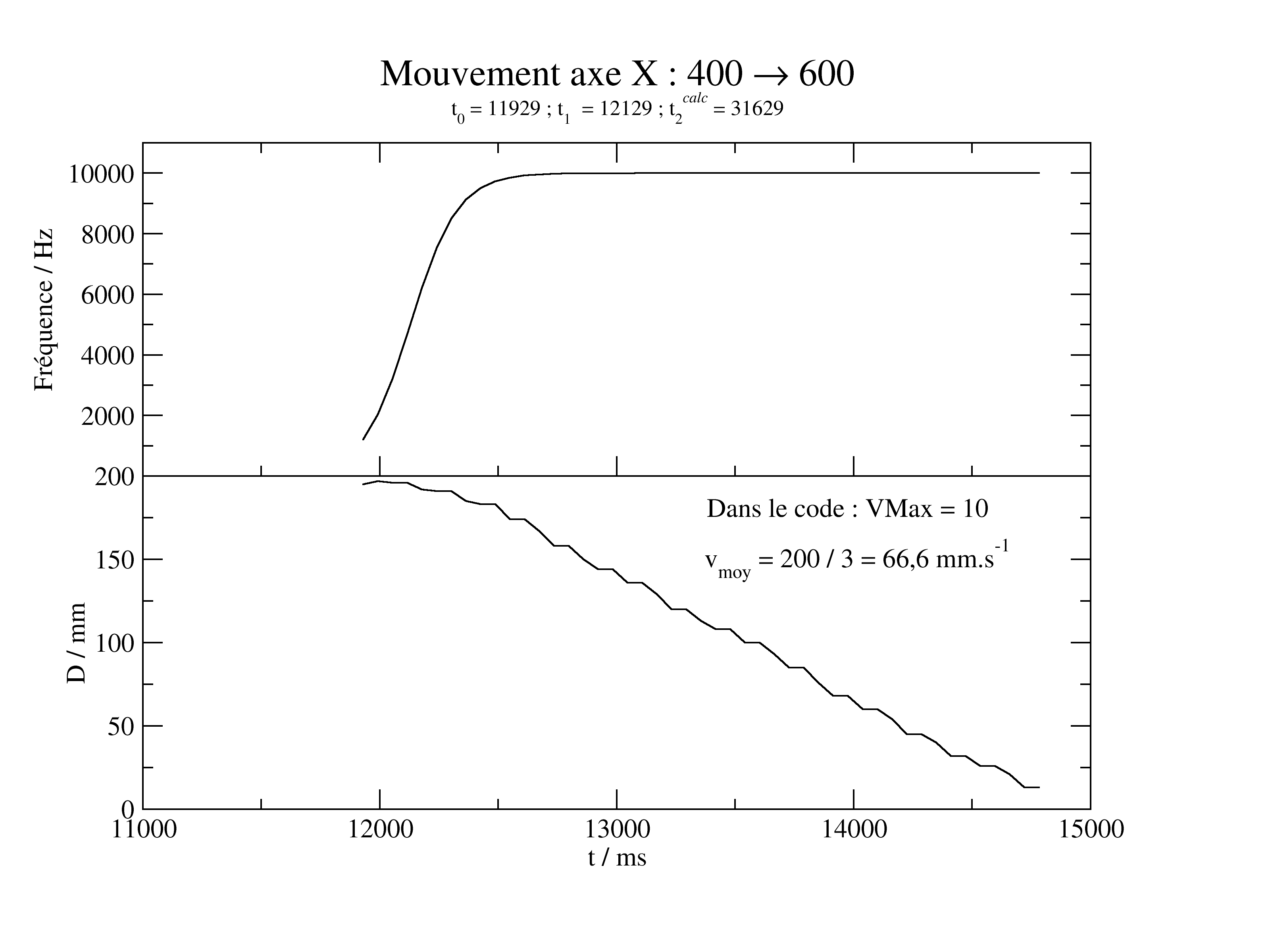
Pour améliorer le déplacement en X, j'extrapole le temps de parcours pour une fréquence 10 kHz (cf. cette étape) :

J'obtiens 12 s. A partir de toutes ces valeurs, je calcule la vitesse en fonction de la fréquence pour chaque fréquence : calcul_rapport_v-f.csv

$$ v \approx 8,0\times10^{-6} f$$

où la vitesse et en m.s^-1 et la fréquence en Hz.

Pour 10 kHz, on observe en effet à peu près 8 cm.s^-1.

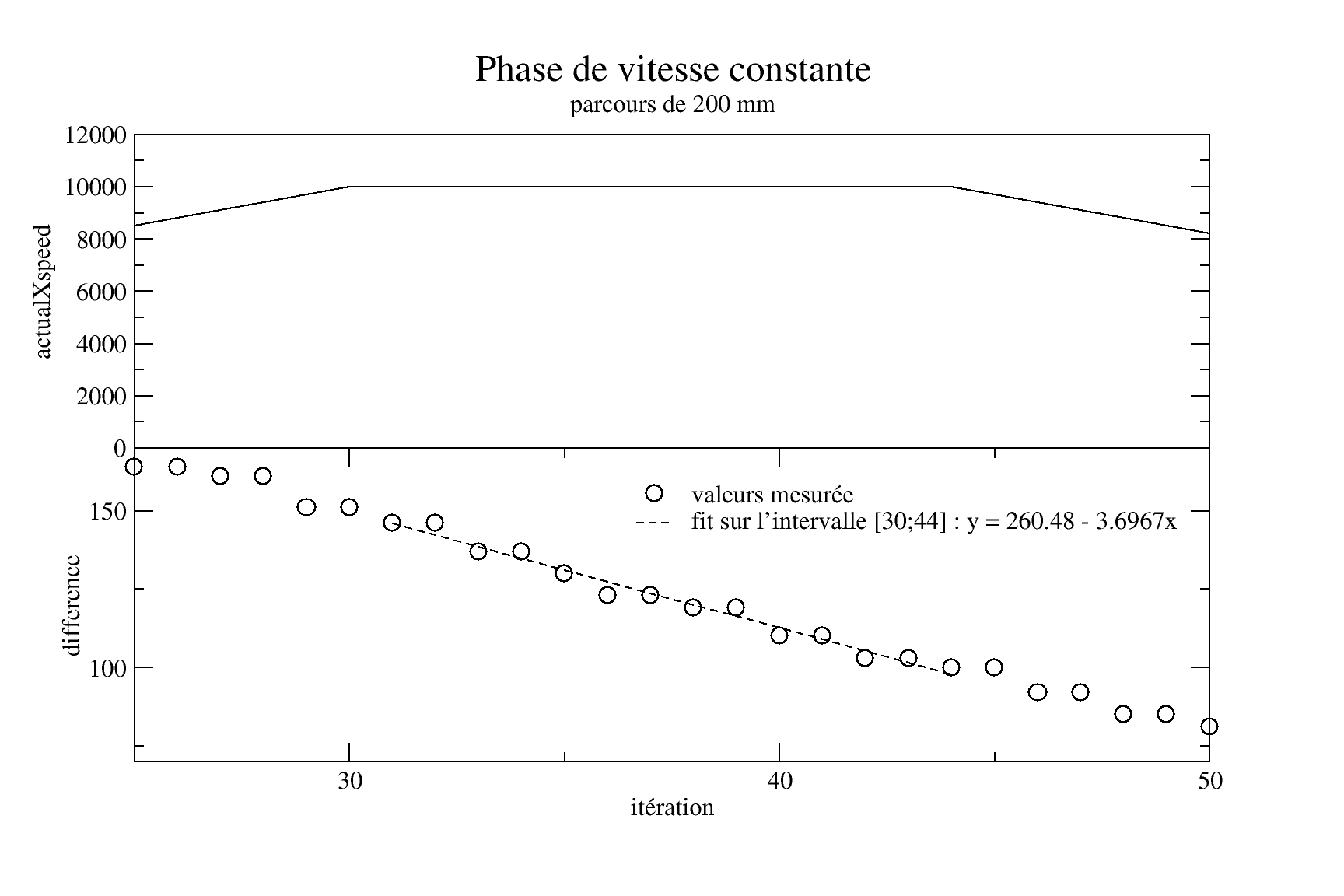
Ainsi, dans la phase de déplacement uniforme, on se rapproche du but de 3,69 mm par itération, soit 21 itérations par secondes, soit 46 ms par itération (qu'on pourrait vérifier...). 

L'idée est donc (si la distance le permet) d'avoir une accélération, une vitesse uniforme, puis une décélération : 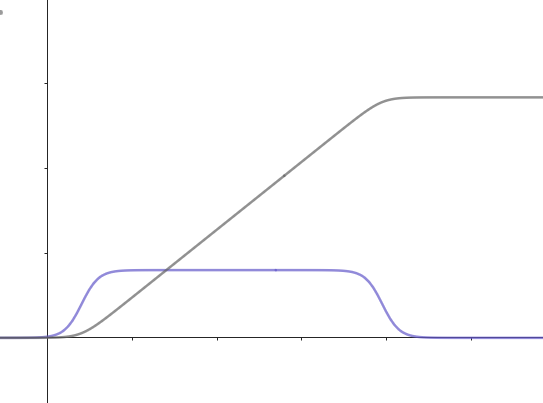en bleu : la vitesse, qui atteint un plateau, et en gris, la position, en fonction du temps.

La courbe bleue peut se modéliser de nombreuses façons. La plus évidente est celle d'une différence entre deux distributions de Fermi-Dirac :

$$ g_1(t) = {1\over{ 1+e^{a(t_1-t)}}} ; \hspace{2cm} g_2(t) = {1\over{ 1+e^{a(t_2-t)}}}  $$

et

$$ V(t) = V_{\rm max}\left( g_1(t) - g_2(t)\right) $$

En intégrant, on obtient :

$$ x(t) = \int_{\tau=0}^{\tau = t} V(t){\rm d}\tau = V_{\rm max} \left[ \ln( 1+e^{a(t_1-t)}) - \ln( 1+e^{a(t_2-t)}) \right] + C $$

La constante d'intégration C s'identifie à x(0).

Or, dans l'approximation limite $$a\rightarrow\infty$$

$$t_2 = t_1 + {{ x_1 - x_2}\over{V_{\rm max}}}$$

On a donc tout pour, au début de smoveXto : 

1. Fixer a et t₁
2. Calculer t₂
3. Tabuler, en fonction de t, les valeurs de x, au mm près.
4. En fonction de t, calculer les valeurs de v.
5. Puis pendant smoveXto prendre la valeur de x (ou t si c'est plus commode) et imposer v.

La feuille Geogebra de mes errements

Au final, on fait deux parcours tests pour régler les paramètres t1 et V_max. 

On fixe a = 0,01 et t₁ = t₀ + 100

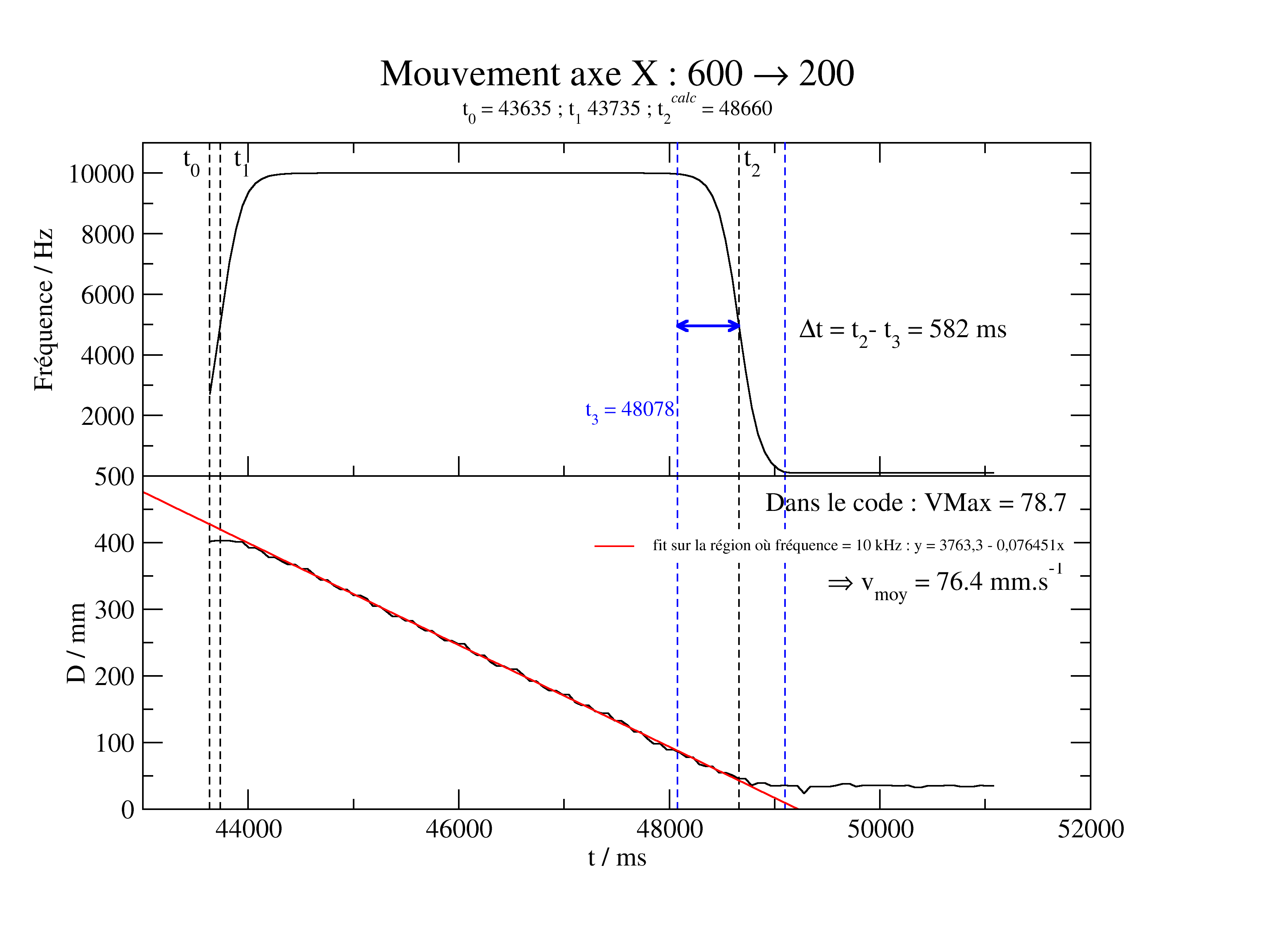
 D'abord grossièrement (à gauche, avec un arrêt brutal) puis finement (à droite) :

On déduit de la V_max = 76,4 mm.s^-1 (précédemment estimé à 80), et un temps d'accélération/décelération de 2x580 = 1160 ms

La distance restant à parcourir au début du freinage (dans la figure de droite) est de 84mm.

On en déduit donc que t₁ était sous estimé.