Retour sur la vitesse en X

Pour améliorer le déplacement en X, j'extrapole le temps de parcours pour une fréquence 10 kHz (cf. cette étape) :

J'obtiens 12 s. A partir de toutes ces valeurs, je calcule la vitesse en fonction de la fréquence pour chaque fréquence : calcul_rapport_v-f.csv

$v \approx 8, 0 \times 10^{- 6} f$

où la vitesse et en m.s^-1 et la fréquence en Hz.

Pour 10 kHz, on observe en effet à peu près 8 cm.s^-1.

Ainsi, dans la phase de déplacement uniforme, on se rapproche du but de 3,69 mm par itération, soit 21 itérations par secondes, soit 46 ms par itération (qu'on pourrait vérifier...).

L'idée est donc (si la distance le permet) d'avoir une accélération, une vitesse uniforme, puis une décélération : 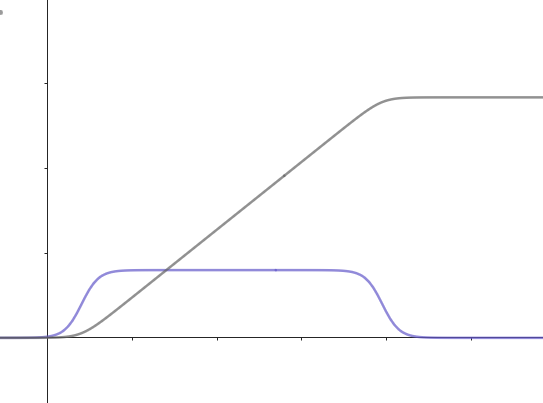en bleu : la vitesse, qui atteint un plateau, et en gris, la position, en fonction du temps.

La courbe bleue peut se modéliser de nombreuses façons. La plus évidente est celle d'une différence entre deux distributions de Fermi-Dirac :

$g_{1} (t) = \frac{1}{1 + e^{a (t_{1} - t)}}; g_{2} (t) = \frac{1}{1 + e^{a (t_{2} - t)}}$

$V (t) = V_{m a x} (g_{1} (t) - g_{2} (t))$

En intégrant, on obtient :

$x (t) = \int_{τ = 0}^{τ = t} V (t) d τ = V_{m a x} [\ln (1 + e^{a (t_{1} - t)}) - \ln (1 + e^{a (t_{2} - t)})] + C$

La constante d'intégration C s'identifie à x(0).

Or, dans l'approximation limite $a \to \infty$

$t_{2} = t_{1} + \frac{x_{1} - x_{2}}{V_{m a x}}$

On a donc tout pour, au début de smoveXto :

Fixer a et t₁
Calculer t₂
Tabuler, en fonction de t, les valeurs de x, au mm près.
En fonction de t, calculer les valeurs de v.
Puis pendant smoveXto prendre la valeur de x (ou t si c'est plus commode) et imposer v.

La feuille Geogebra de mes errements

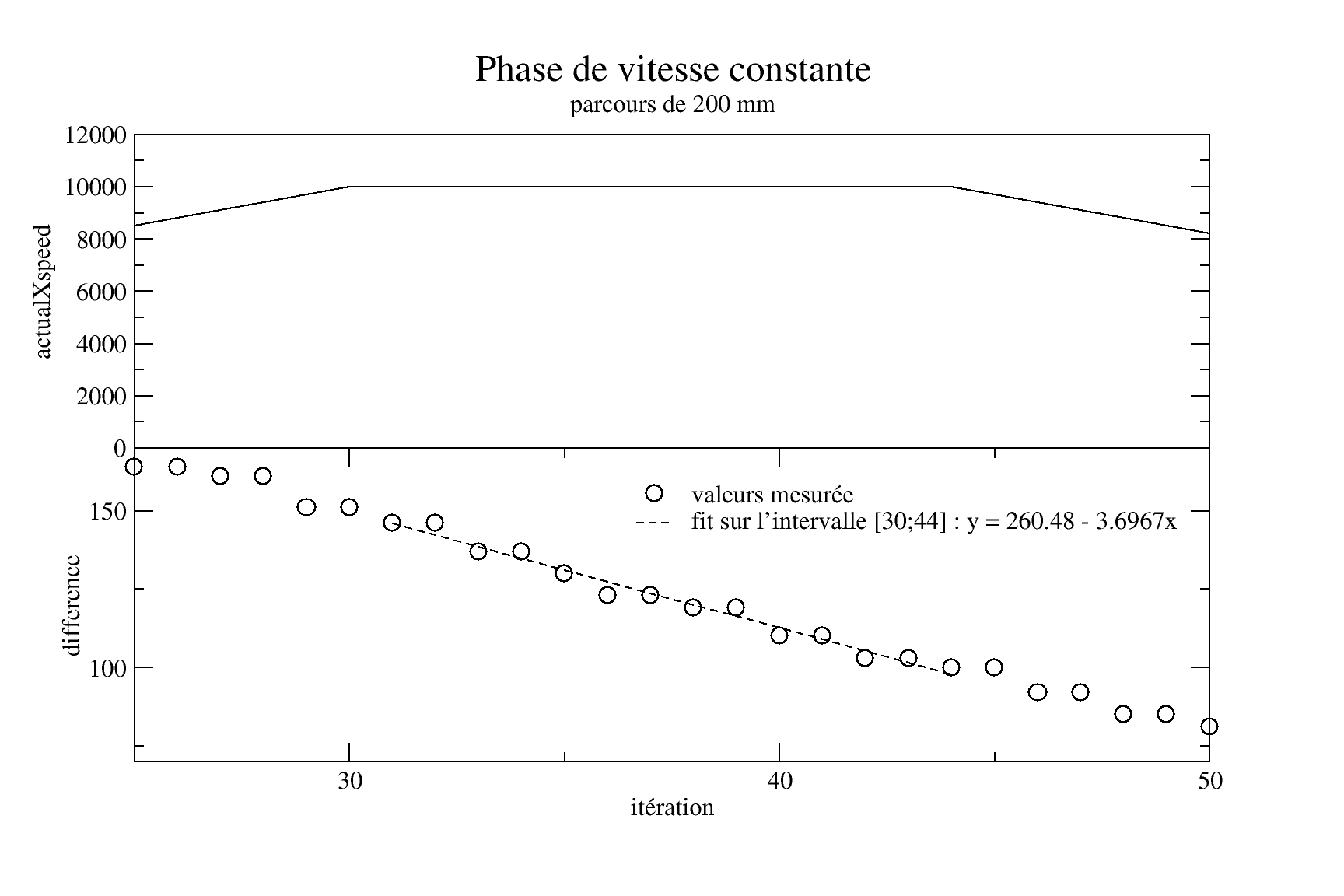
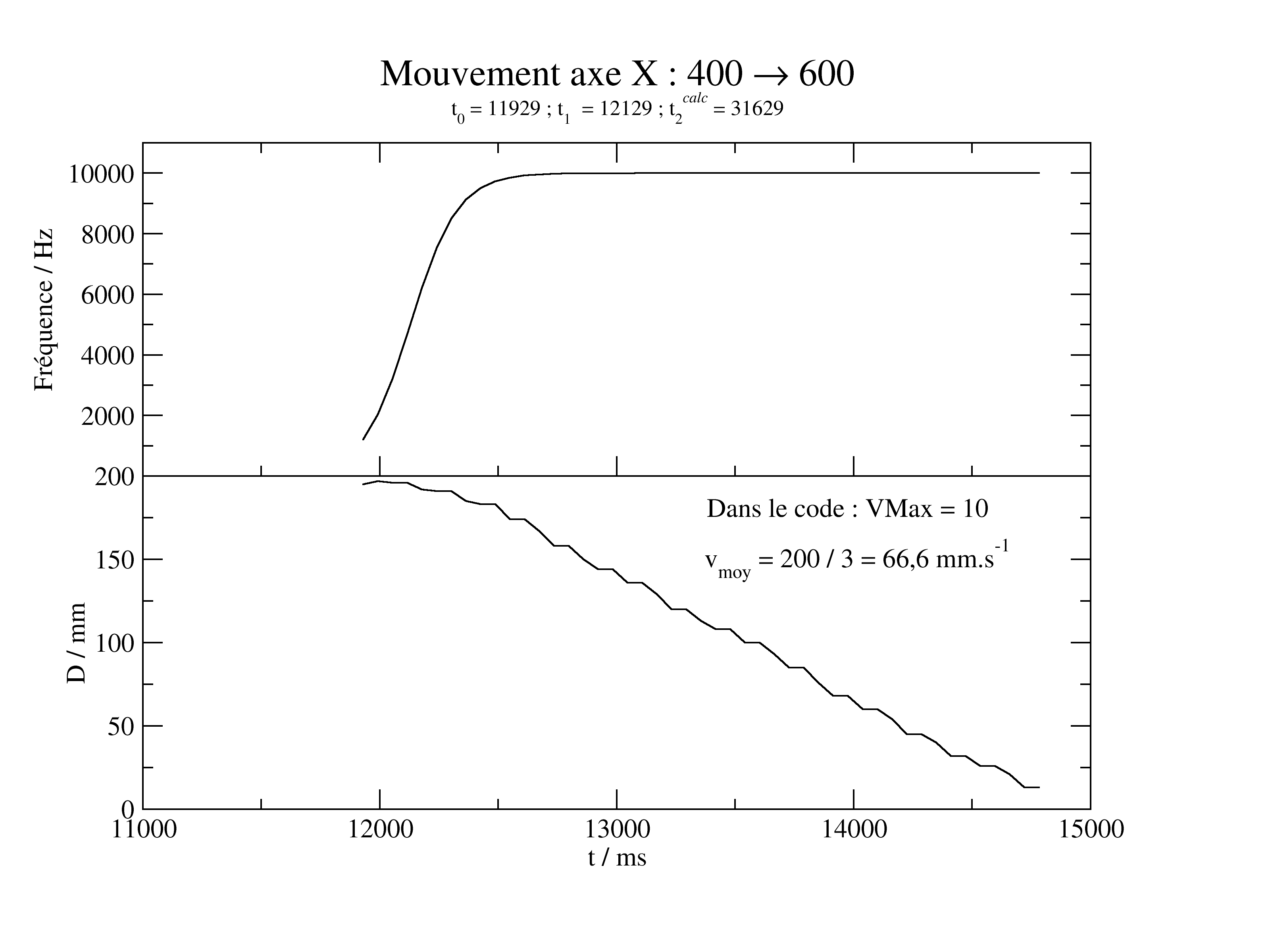
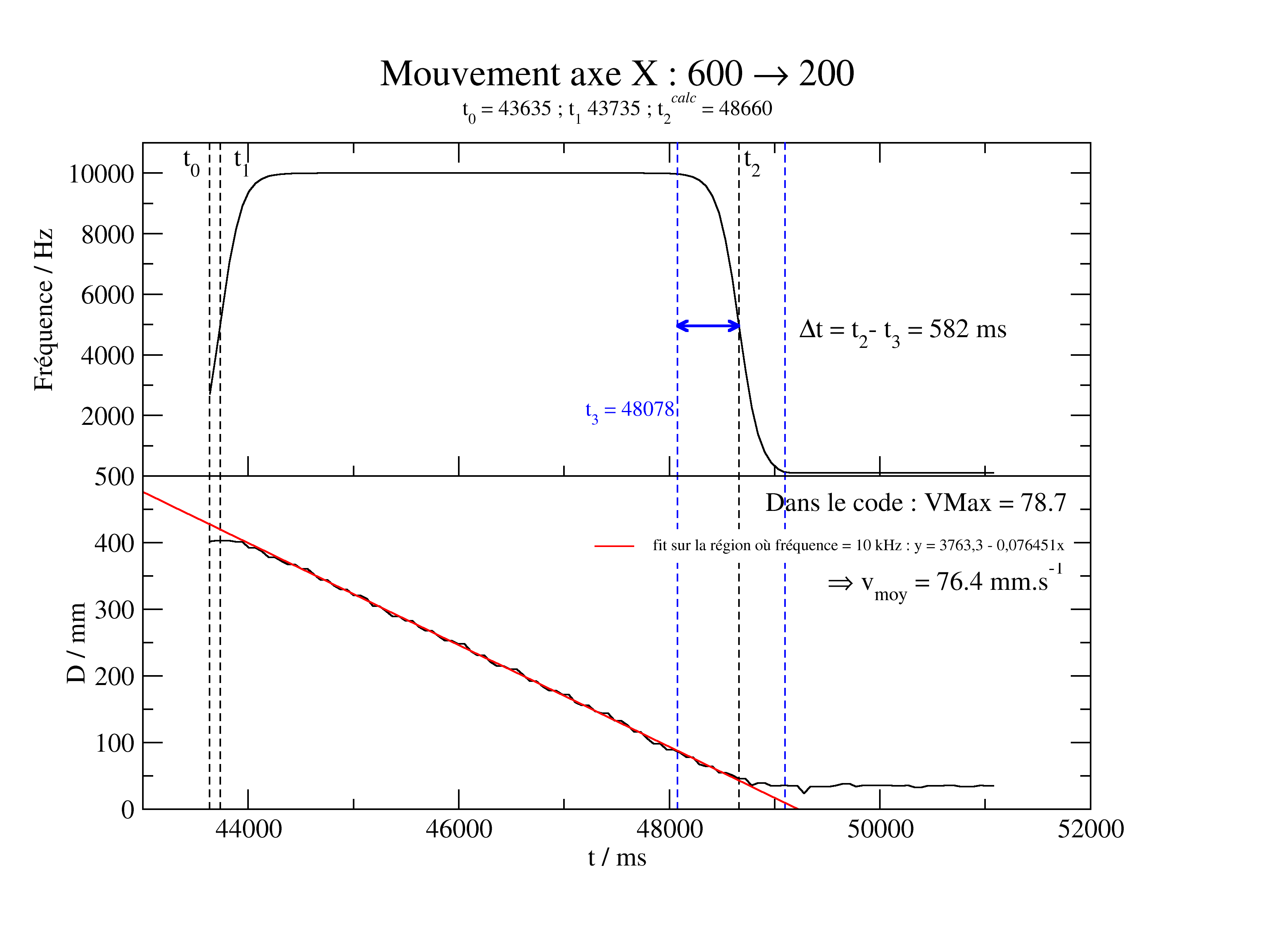
Au final, on fait deux parcours tests pour régler les paramètres t1 et V_max.

On fixe a = 0,01 et t₁ = t₀ + 100

D'abord grossièrement (à gauche, avec un arrêt brutal) puis finement (à droite) :

On déduit de la V_max = 76,4 mm.s^-1 (précédemment estimé à 80), et un temps d'accélération/décelération de 2x580 = 1160 ms

La distance restant à parcourir au début du freinage (dans la figure de droite) est de 84mm.

On en déduit donc que t₁ était sous estimé.

Après avoir un peu galéré et discuté avec les étudiants de TopAéro (qui sortiraient volontiers l'artillerie lourde), je reviens à l'idée d'indexer la fréquence (et donc la vitesse) sur la position mesurée.

On crée un tableau GLOBAL (sinon la pile réservée aux variables locales explose, même si le tableau ne fait que 40 ko, voir par exemple cette discussion). Le tableau est rempli en précalculant la trajectoire : on itère sur t suivant les explications ci-dessus, et à chaque t, on calcule à la fois v(t) et x(t), obtenu par l'intégration analytique. Dans certains intervalles, on obtient de trop nombreuses valeurs de x très proches les unes des autres. Mais comme la mesure de distance retournera un entier, c'est tout à fait inutile d'avoir une telle précision : on écrase donc les valeurs calculées de la vitesse jusqu'à ce qu'on passe à la distance entière suivante (je ne sais pas si c'est très clair).

int nb = 2000;

//Serial.println("preparing f array");
for (int i = 0 ; i < 2000 ; i++) {
  f[i] = 0;
}

int step = ( tf - t0 ) / nb ;

double deltat1 = (double) (t1 - t0) ;
double deltat2 = (double) (t2 - t0) ;
double cc = currentDistance - sens * VMax * ( log (1.0 + exp(a*(deltat1))) - log (1.0 + exp(a*(deltat2)))) / 10 ;

for (int i = 0 ; i < nb ; i++) {
  int t = t0 + i * step;
  double deltat1 = (double) (t1 - t) ;
  double deltat2 = (double) (t2 - t) ;
  double df = FreqMax * ( 1.0 / ( 1.0 + exp(a * deltat1) ) - 1.0 / ( 1.0 + exp(a * deltat2) )) ;
  double dd = sens * VMax * ( log (1.0 + exp(a*(deltat1))) - log (1.0 + exp(a*(deltat2)))) / 10 + cc ;

  f[constrain((int) dd, 0, 2000)] = constrain((int) df, FreqMin, FreqMax);
}

Ensuite, la modification de la fréquence se fait de manière directe :

    currentDistance = Xsensor.getDistance();
    int actualFreq = f[currentDistance];
    ledcSetup(pwmChannelX, actualFreq, 8);
    ledcSetup(pwmChannelY, actualFreq, 8);

Par ailleurs, c'est une bonne occasion de rappeler comment récupérer les infos venant du port série sur un Mac, autrement qu'en faisant des copier-coller à partir de l'IDE. Bien sûr, on peut installer des applications comme CoolTerm, ou SerialTools.

Mais on peut aussi faire les choses à la mode unix :

(stty speed 115200 >/dev/null && cat) </dev/cu.usbserial-54D80285741 | tee serial.log

C'est officiel, j'ai ré-inventé la roue, et je me suis cassé la tête pour rien : un trapèze simple (accélération / décelérations constantes) suffirait largement (discussion avec Guillaume Morel qui me suggère de lire le papier de Hogan et Flash sur le minimum jerk et le livre de Dombre et Khalil (ainsi que son cours).

C'est d'ailleurs ce qui est fait sans le dire dans la version précédente de la routine smoveXto.

Soit a l'accélération, x_i et x_f les positions et V_max. Il existe deux types de trajets : ceux pendant lesquels la vitesse maximale va être atteinte parce que la distance est suffisante (2) ; ceux pendant lesquels il faut commencer à freiner avant de l'avoir atteinte (1).

Cas 1 : x_f-x_i est insuffisante pour atteindre V_max.

$v (t) = a t p u i s v (t) = v (t_{1 / 2}) - a t$

soit $x (t) = a t^{2} + x_{i} p u i s x (t) = x_{i} + \frac{x_{f} - x_{i}}{2} + a t_{1 / 2}^{2} - a t^{2}$

On trouve t_1/2:

$x (t_{1 / 2}) = \frac{x_{f} - x_{i}}{2} = a t_{1 / 2}^{2} + x_{i}$

d'où $t_{1 / 2} = \sqrt{\frac{x_{f} - x_{i}}{2 a}}$

A la limite, où x_f-x_i est suffisante, on atteint V_max pile pour t_1/2 :

$V_{m a x} = a t_{1 / 2} = a \sqrt{\frac{x_{f} - x_{i}}{2 a}} = \sqrt{a \frac{x_{f} - x_{i}}{2}}$

Cas 2 : si x_f-x_i est supérieure à la valeur trouvée ci-dessus, alors il faut définir t₁ et t₂ qui délimitent le plateau parcouru à vitesse max.

Retour sur la vitesse en X

No Comments