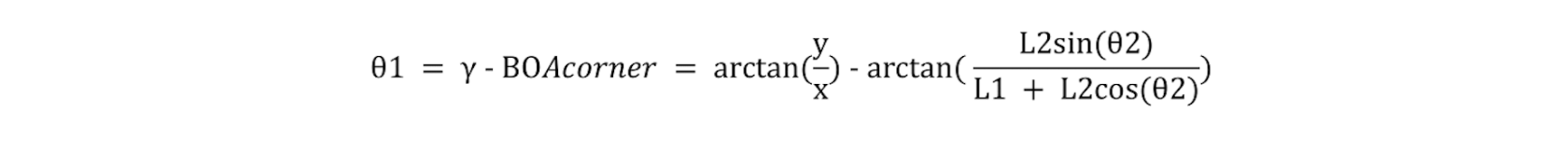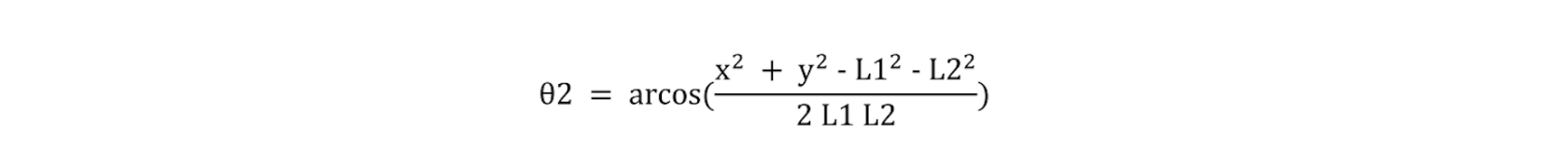Projet ROB3: Rami, Yannis, Vasilis
LineaScribe Robot
Informations
Membres
| Nom Prénom | |
| TOBBAL Yannis | tobbalya@gmail.com |
| ARIDI Rami | rami.aridi@etu.sorbonne-universite.fr |
| SKARLEAS Vasilis | vasileios.skarleas@etu.sorbonne-universite.fr |
Cursus
Polytech 3eme année | Spécialité: Robotique
Délais
Début: 14/02/24 | Fin: 23/05/24
But, objectifs et contexte
But
Le but est de créer un robot capable de dessiner différentes formes sur une feuille de papier. Il doit pouvoir réaliser des formes préprogrammée ainsi qu'être contrôlé manuellement.
Le robot est fixé sur un support carré horizontal comportant une zone de dessin de 10*10 cm. Il y a 2 exercice qu'il doit réussir. En outre, le robot faut être capable de répondre au cahier des charges disponible ici.
Exercice 1
Dessiner des formes prédéfinies
Le robot doit être capable de réaliser en 10 +- 0.2 secondes:
-Une ligne droite de 5cm
-Une ligne droite de 5cm en pointillés
-Un cercle de 2.5cm de rayon
-Un cercle de 2.5cm de rayon en pointillés
Exercice 2
Permettre à un utilisateur de dessiner
L'utilisateur doit être capable d'utiliser le robot pour dessiner la forme qu'il veut sur la zone de dessin. Le robot est contrôlé par un joystick qui doit donc être doté des fonctions utilisés dans l'exercice 1 (Déplacement, relever le stylo etc...)
Besoins
Il faut donc créer un robot qui:
- Maintienne un effecteur (le stylo) afin de dessiner
- Se déplace:
- Dans un plan horizontal: Créer les formes
- Verticalement: Dessiner ou non, pour les pointillés
- Enregistre des formes prédéfinies
- Soit capable d'être contrôlé précisément par le joystick
Matériel
Les moyens qu'on a à notre disposition sont les suivantes:
- Un crayon
- Interface de commande :
- Une carte arduino UNO avec câble USB-B;
- Un joystick:
- Une platine de protoypage;
- Alimentation régulée 5V ;
- Câbles, LEDs, boutons poussoirs, résistances.
- Motorisation :
- Deux servomoteurs HS422 180°;
- Un servomoteur Emax ES08A 180°.
- Mécanique :
- Matière PLA pour impression 3D;
- Feuilles MDF : 3mm et 6mm d'épaisseur;
- Vis et écrous : M2, M2.5, M3, M4.
- Roulements et axes de diamètre 4mm.
- Informatique
- Ressources CAO.zip contient les fichiers Solidworks pour les deux modèles de servomoteurs
- datasheets.zip contient les documentations de quelques-uns des composants fourni
Machines utilisées
Utilisation de l'impression 3D pour des pièces sophistiquée et éventuellement de la technologie de découpe laser pour les autres pièces.
Matière consommée:
MDF: 64 cm3 (Bras) + 302 cm3 (Tour): 366 cm3 total
PLA: 7.3 cm3 (Effecteur) + 9 cm3 (Actionneur) : 16.3 cm3 total
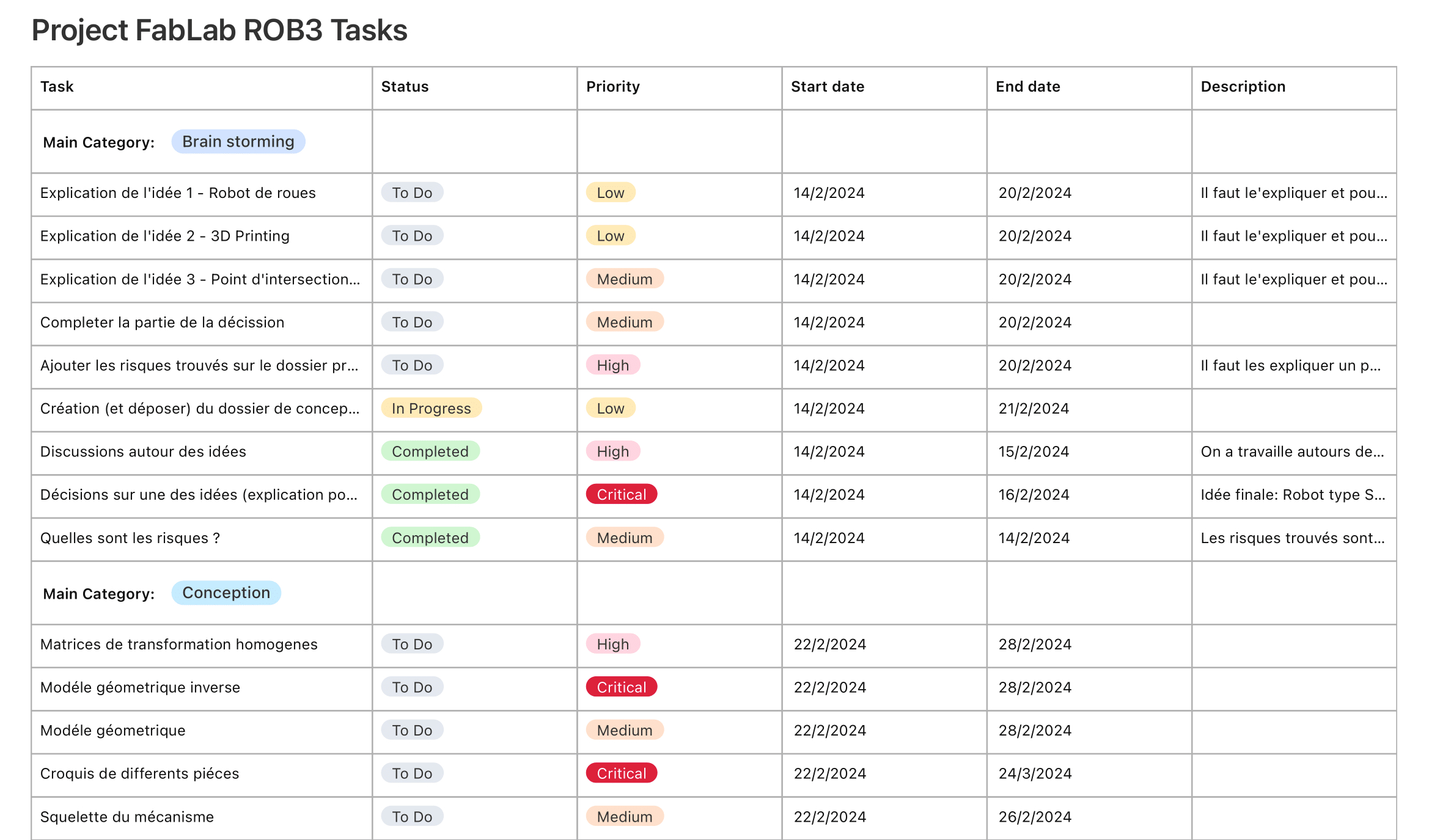
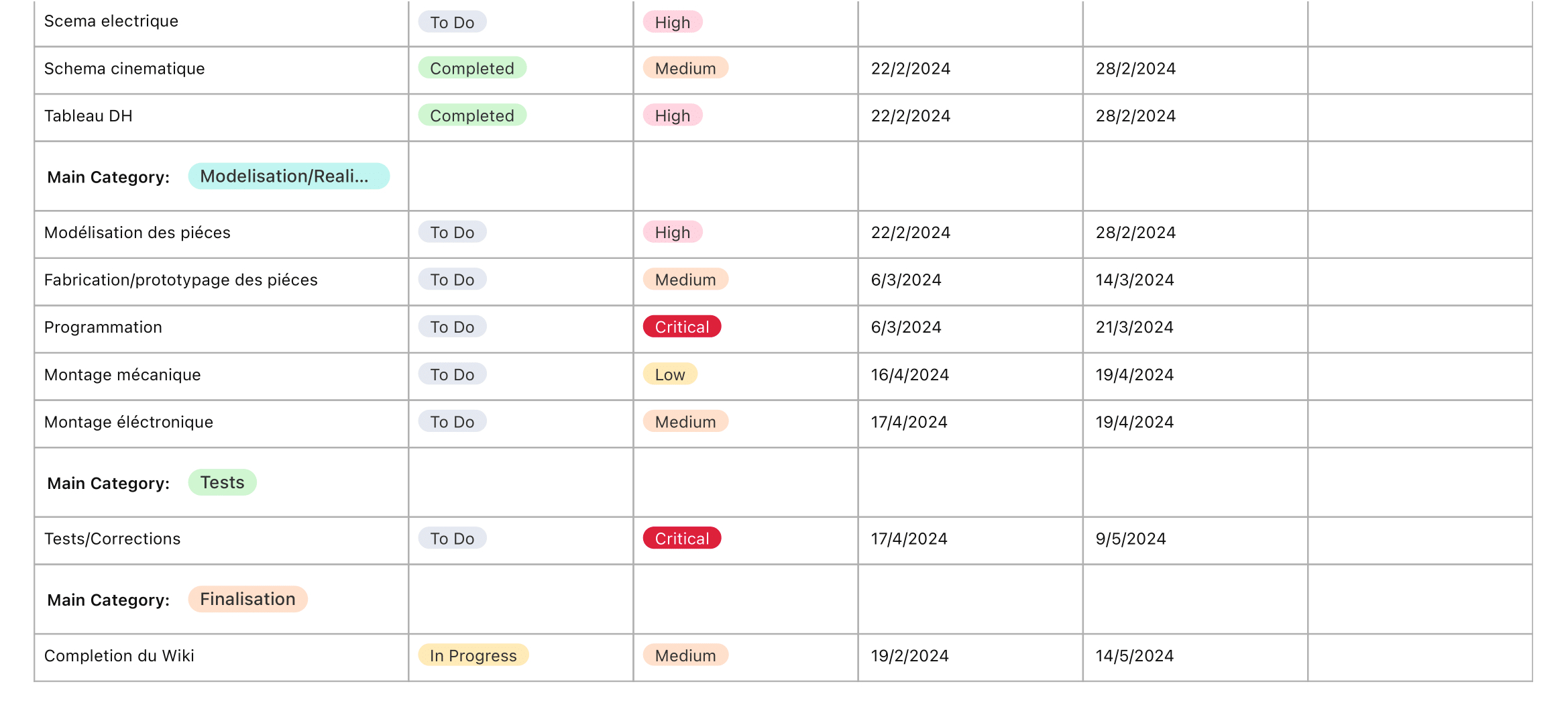
Diagramme de GANTT
Il y a un lien interactif qui est mis à jour à chaque modification via https://airtable.com/appVydj1BDLSFj432/shrm5Cjk0diMBPmgL
Nota bene
Ce diagramme de GANTT est donnée à titre indicatif
Project FabLab ROB3 Tasks (GANTT).pdf
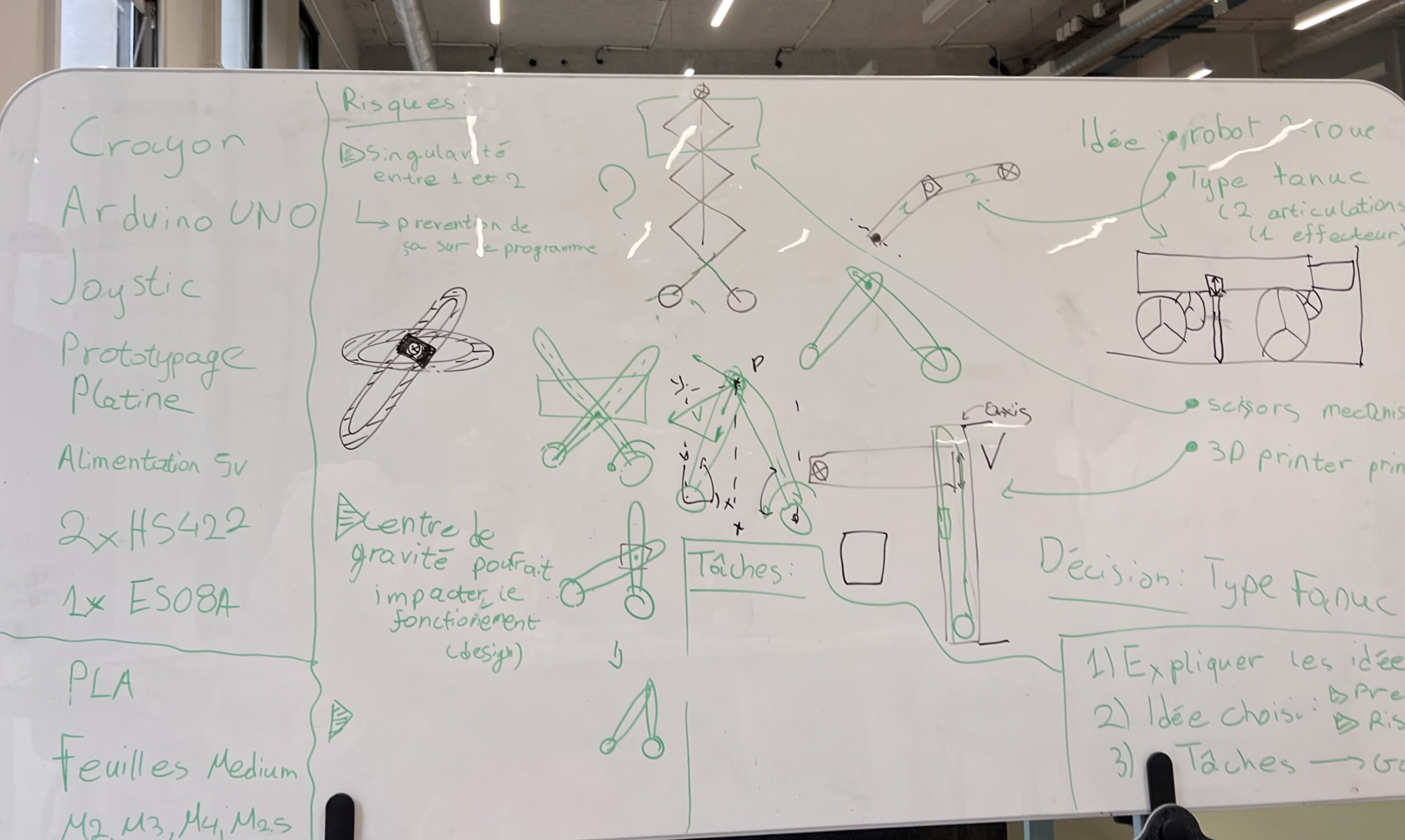
Étape 1: Brainstorming, idées de réalisation et analyse des risques
Durant notre brainstorming: nous eûmes 5 idées que nous avons ultimement rejetées:
Idée 1 - Robot de roues
Principe:
Un robot sur deux roues motorisées. Il peut faire de rotations en faisant tourner ses roues dans des directions opposées
- Le stylo est attaché au centre de de la plateforme.
- Les roues seraient contrôlées grâce aux 2 servomoteurs HS422 d'une façon similaire au robot E-PUC. Les servomoteurs sont connectés à la plateforme et aux roues via des biellettes ou des engrenages.
- Un servomoteur ES08A est utilisé pour contrôler le mécanisme de levée et de descente du stylo. Ce servomoteur est plus petit que les HS422 et peut être monté sur la plateforme à proximité du stylo.
Croquis:
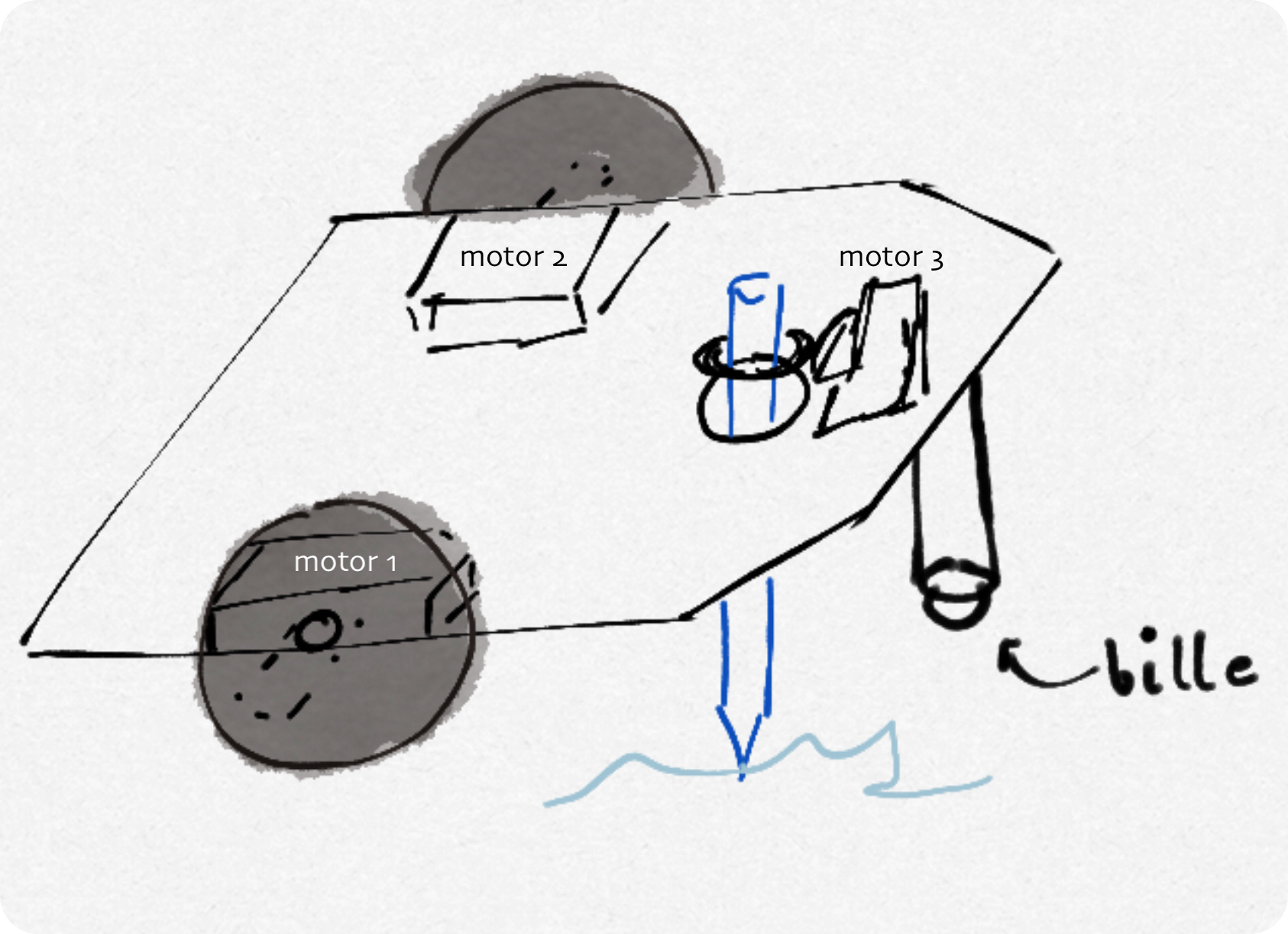 Figure 2: Croquis du robot de roues (type voiture avec une bille pour la stabilisation)
Figure 2: Croquis du robot de roues (type voiture avec une bille pour la stabilisation)
Avantages:
- Le robot est facile à contrôler avec un joystick (important pour la réalisation de l’exercice 2)
- Sa construction et modélisation est simple
Inconvénients:
- On ne peut pas réaliser de trajectoires complexes. Le robot ne peut pas suivre des trajectoires complexes sans l'aide de capteurs odométrique.
- L'utilisation des servomoteurs empêcherait de faire rouler le robot indéfiniment. Cela ne serait pas un problème avec l'exercice 1. L'exercice 2 pourrait se révéler impossible à faire (Prenons par exemple un cas hyperbolique et fantaisiste: La forme à dessiner au joystick est une réplique de la Joconde. Le robot ne pourrait jamais faire ceci). Pour dépasser cet obstacle, il faudrait utiliser de roues avec une diamètre assez grande entraînant des complications aux glissements sur la surface.
Idée 2 - Robot XY (cartésien)
Principe:
Un système similaire au fonctionnement d'une imprimante 3D:
- A l'aide d'un système de bielle manivelle, les deux servomoteurs HS422 commandent des liaisons glissières sur les axes x et y.
- La bielle tenant le stylo est elle même tenue par une bielle. Cette dernière se positionne sur la coordonnée de son axe, tandis que la bielle de l'effecteur choisit alors la deuxième coordonnée du point.
- Le servomoteur ES08A commande la levée et descente du stylo
Croquis:
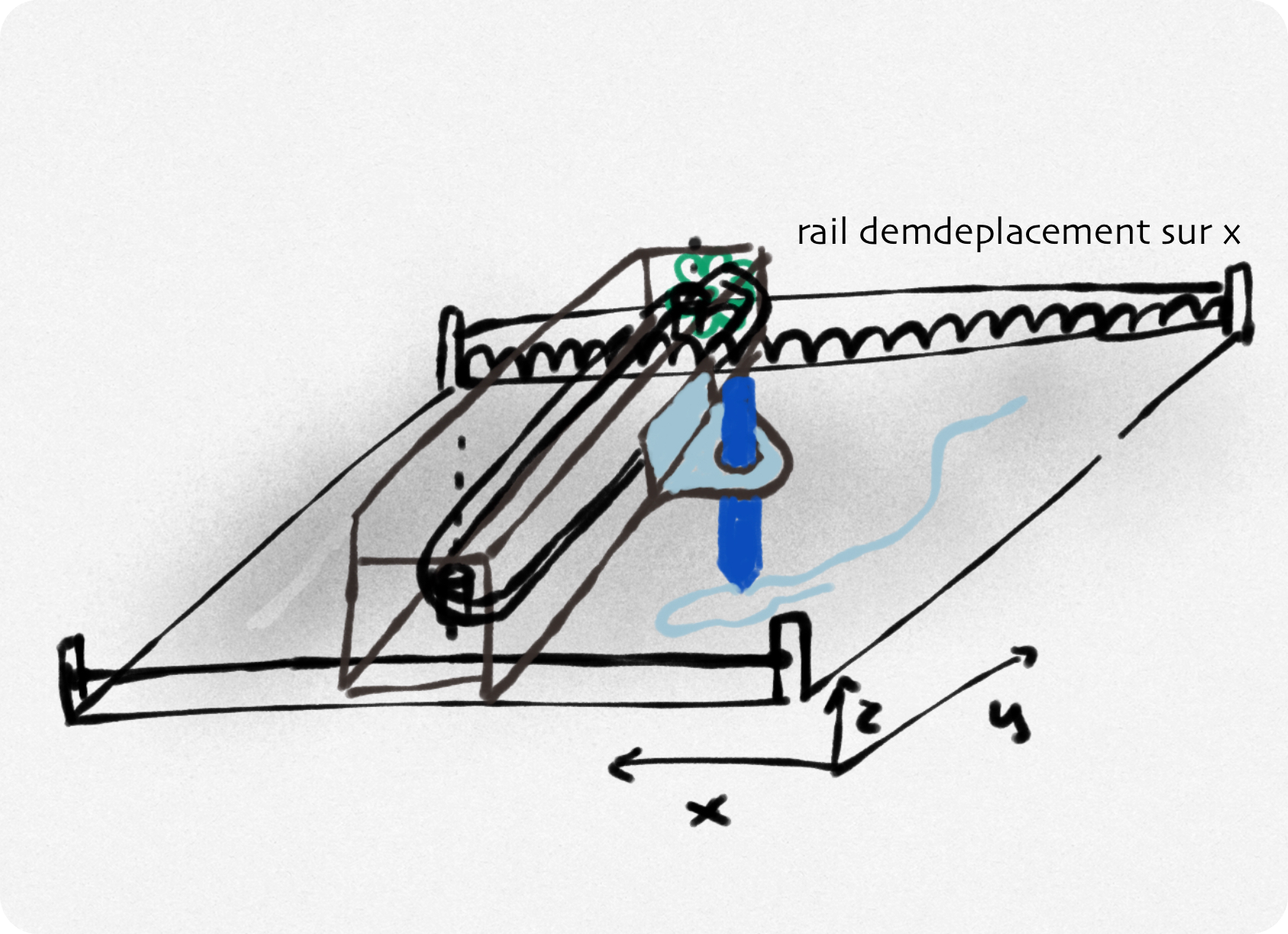 Figure 3: Le croquis d'un robot cartésien
Figure 3: Le croquis d'un robot cartésien
Avantages:
- Cette solution ne présente pas de singularités dans sa configuration. De plus, les calculs sont simplifiés par le fait qu'on ne réfléchisse que sur le plan cartésien. Ce qui signifie qu'il peut atteindre toutes les positions du plan cartésien.
- Ce système permet un mouvement fluide et précis du stylo.
- Les calculs pour contrôler le robot sont simplifiés par le fait qu'on ne réfléchit que sur le plan cartésien sans faire ce changements de bases.
Inconvénients:
- Le système de bielle-manivelle peut être plus lourd qu'un système à roues motorisées, ce qui peut affecter la performance du robot.
- Le système de bielle manivelle pourrait se révéler trop massif pour le robot.
- La solution consommerait beaucoup de matière
Idée 3 - Scissors mecanism
Principe:
Inspirés du "Scissors mechanism", on voudrait attacher deux servomoteurs à la base du mécanisme et un système de commande d'actionneur au point "STYLO". Cette solution présente des avantages telles que :
Croquis:
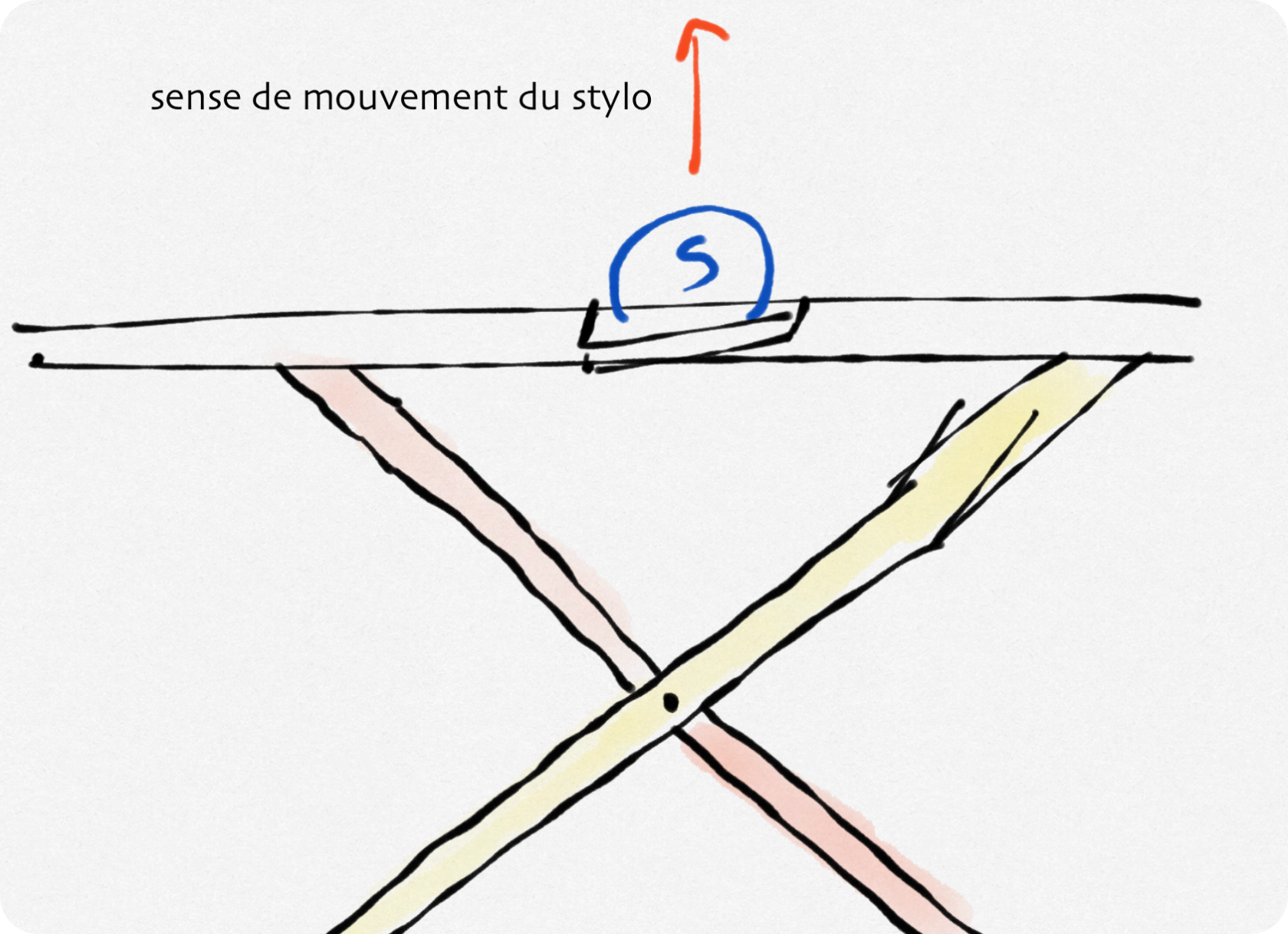 Figure 4: Démonstration du mécanisme de ciseaux
Figure 4: Démonstration du mécanisme de ciseaux
Avantages:
- Le mécanisme "Scissors" permet d'avoir un espace d'écriture plus grand que les systèmes à roues motorisées ou à bielle-manivelle. Cela est dû à la tendance du mécanisme à s'étendre.
- De plus, ce mécanisme est particulièrement adapté à la création de cercles. La rotation des bras permet de dessiner des cercles de différentes tailles avec précision.
- En outre, le mécanisme "Scissors" permet de dessiner des lignes droites très précises dans le sens du mouvement du stylo.
Inconvénients:
- Malheureusement, cette solution présente également un inconvénient. Les mouvements étant plutôt révolutionnaires, créer des lignes droites verticales du stylo semble limité et dans certains cas extrêmes impossible.
Idée 4 - Point d'intersection
Principe:
Le robot sera doté d'un mécanisme de ciseaux alimenté par deux servomoteurs positionnés aux coins de la base d'écriture. Chacun entraînera la rotation d'une poutre, permettant des mouvements de glissement dans les deux directions du vecteur r de rotation,. Le point d'intersection des deux poutres (créant ainsi une liaison glissière complexe) serait équipé du stylo, assurant une couverture totale de la feuille grâce à cette configuration ingénieuse.
Croquis:
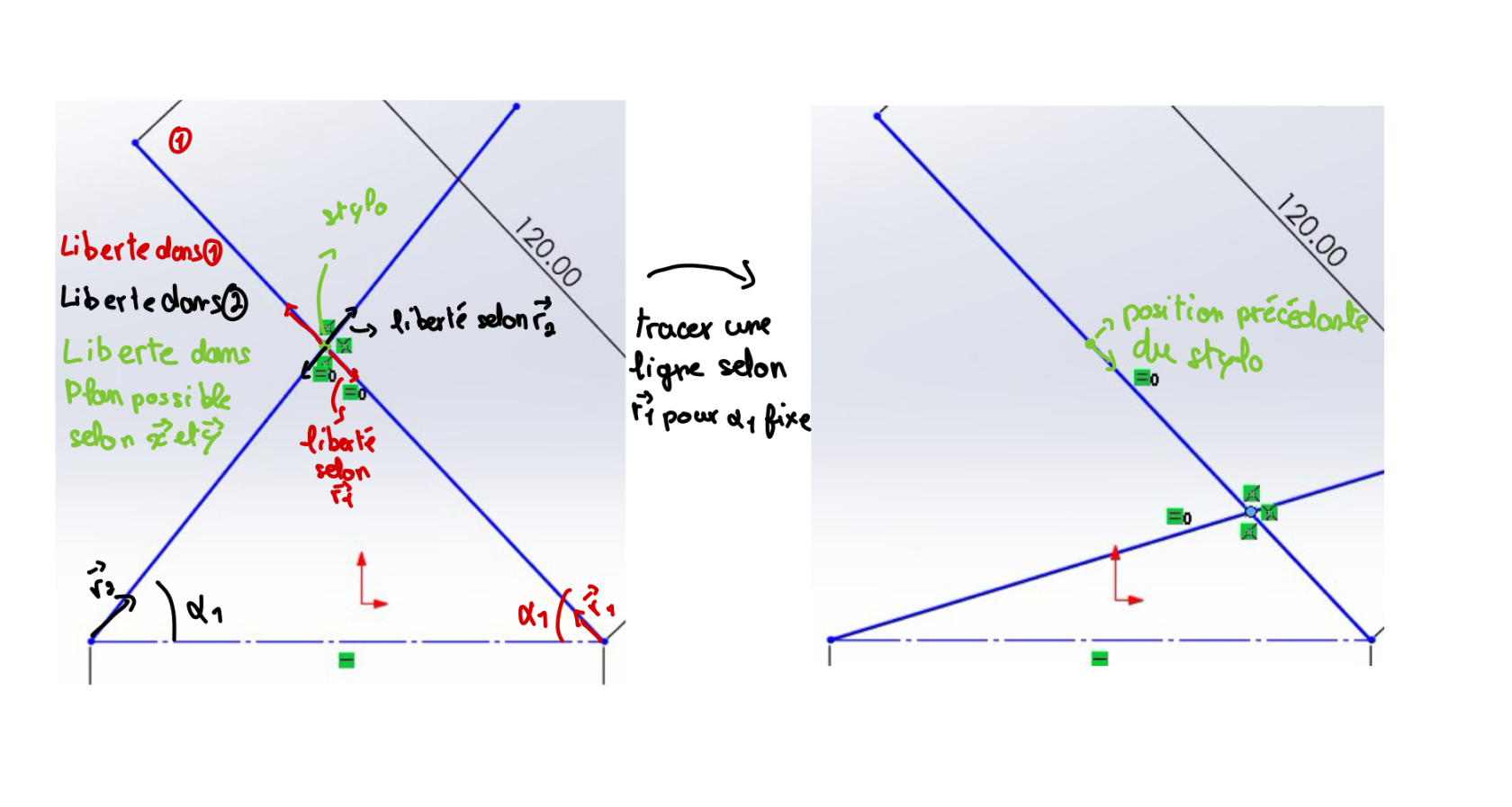 Figure 5: Une conception de l'idée de point d'intersection
Figure 5: Une conception de l'idée de point d'intersection
Inconvénients:
- L'effort tangent au mouvement du stylo généré par une poutre sur l'autre serait extrêmement important, dépassant probablement les limites de faisabilité. La nécessité d'un glissement ultra-lisse, sans aucun frottement, et d'une précision extrême dans les mouvements représente un défi technique considérable.
Idée 5 - Robot type SCARA
Principe:
On a pensé de faire un robot qui a deux axes de rotation verticales et une axe de rotation horizontale. En fait, il y aura deux rotations autour de deux axes Z (Z1 et Z2) verticales et une troisième rotation autour de Z3 qui est perpendiculaire au axe (Z2).
Croquis:
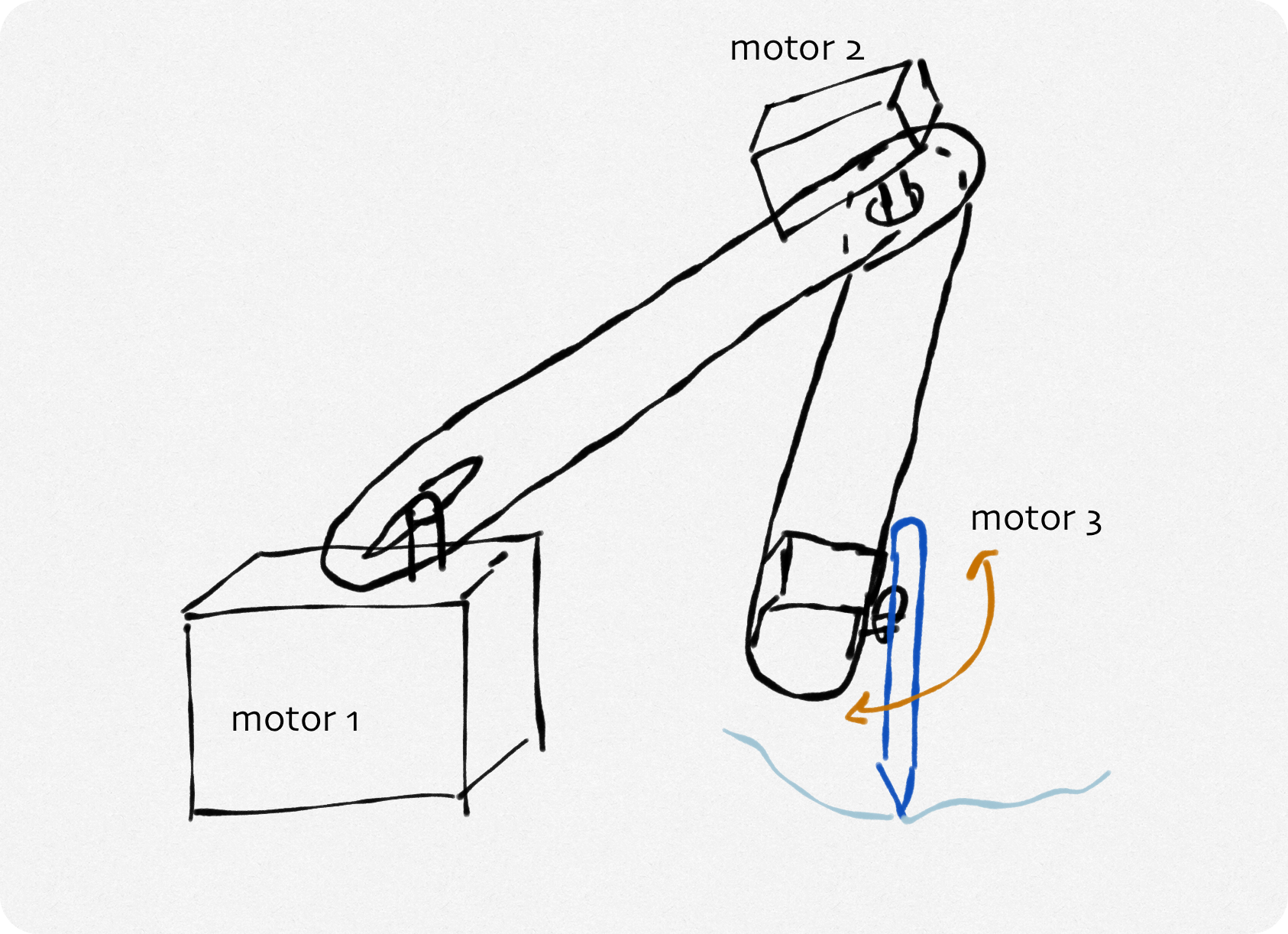 Figure 6: croquis du robot avec 2 dégrées de liberté
Figure 6: croquis du robot avec 2 dégrées de liberté
Avantages:
- C'est un modèle connu du groupe, la partie mathématique est donc plus simple à réaliser
- Il y a beaucoup de manières de retirer de la matière avec une modélisation intelligente.
Inconvénients:
- Poids excessive sur l'endroit du moteur 2, quelque chose qui pourrait impacter la précision de designs. Idéalement, on voudrait trouver une solution qui permettra de déplacer ce moteur sur le corps de la base principale du robot (où se trouve le moteur 1) en utilisant les outils qu'on a à notre disposition.
Idée 6 - Robot parallélépipède
Principe:
Inspiré par le mécanisme du robot type SCARA, on avait une réflexion: "Pourquoi on ne déplace pas le moteur de la 2éme rotation (moteur2), sur le même axe de rotation qui celui du moteur 1. Le résultat du mouvement sera la même tout en ayant déplacé la majorité du poids sur le corps principale du robot.
Croquis:
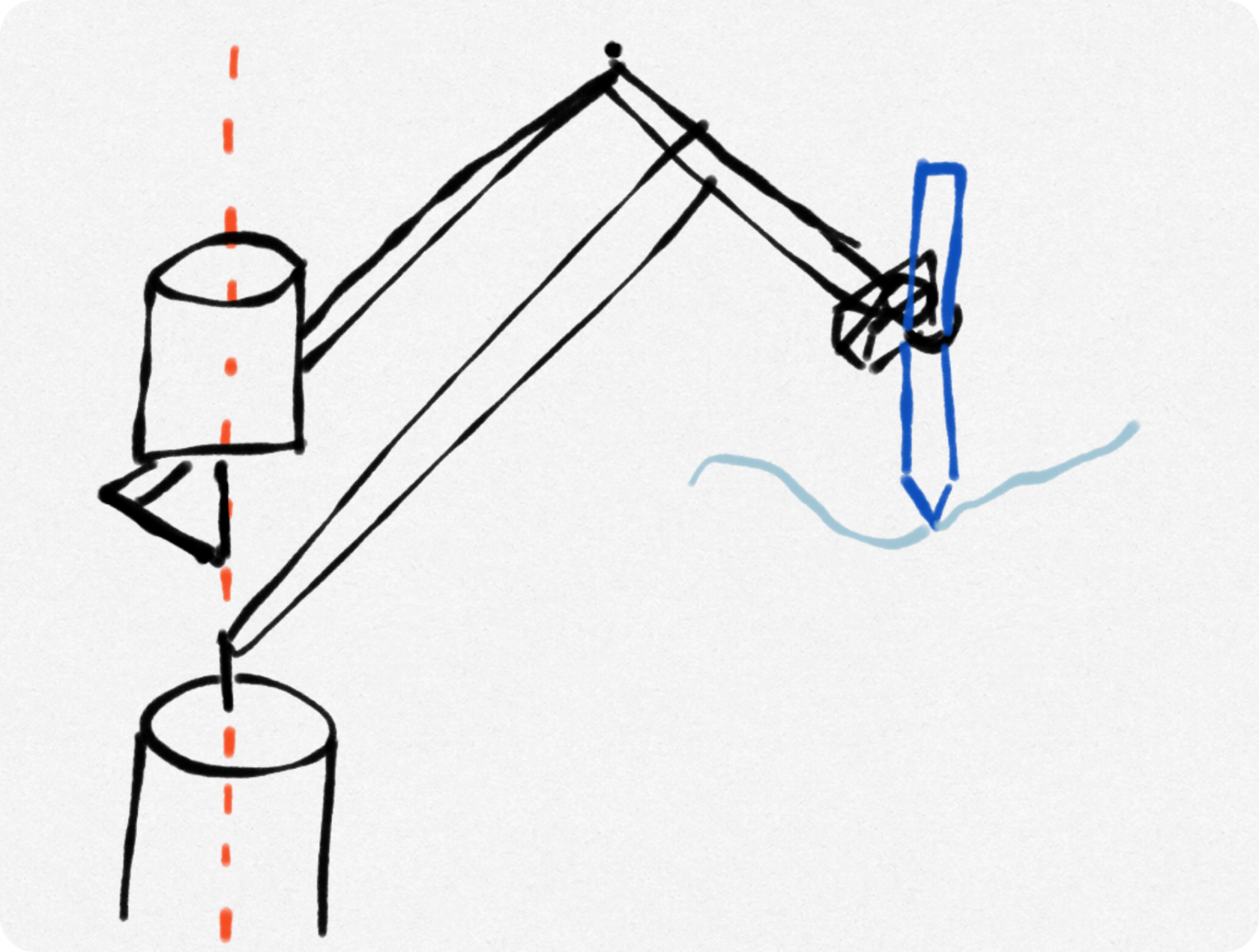 Figure 7: Croquis du robot parallélépipède
Figure 7: Croquis du robot parallélépipède
Avantages:
- Moins de poids sur les articulations mobiles du robot => meilleur précision par rapport l'idée d'avant.
Inconvénients:
- Selon la manière d'expression du modèle géométrique direct, le calcul du modèle géométrique inverse pourrait être compliqué.
- La modélisation des quelques pièces unique pour la réalisation de ce type du robot pourrait augmenter le temps de fabrication et l'utilisation de matière.
Solution retenue
Ayant effectué une évaluation approfondie des différentes alternatives, notre équipe a choisi de privilégier le développement d'un robot type parallélépipède pour la prochaine étape du projet. Cette décision est basée sur plusieurs points clés :
- Robot de roues
- Pour s'assurer de la validité de la trajectoire, il faudrait l’équiper de capteurs odométrique. Nous ne disposons pas de ce matériel
- L'utilisation des servomoteurs empêcherait de faire rouler le robot indéfiniment. Cela ne serait pas un problème avec l'exercice 1. L'exercice 2 pourrait se révéler impossible à faire (Prenons par exemple un cas hyperbolique et fantaisiste: La forme à dessiner au joystick est une réplique de la Joconde. Le robot ne pourrait jamais faire ceci)
- Pour s'assurer de la validité de la trajectoire, il faudrait l’équiper de capteurs odométrique. Nous ne disposons pas de ce matériel
- Robot XY
- Le système de bielle manivelle pourrait se révéler trop massif pour le robot.
- La solution consommerait beaucoup de matière
- Robot "scissors"
- Selon la mécanique de la pièce, la création des lignes droites perpendiculaires du stylo n'est pas toujours possible à cause des mouvements révolutionnaires du mécanisme
- Les déplacement sont limités à des trajectoires bien précises, ce qui rend le contrôle au joystick frustrant.
- Robot intersection
- Il s'agit d'une idée très complète. Cependant, lorsque l'effecteur se trouve à l'extrémité des deux axes de guidage, il faut exercer une force massive pour l'en sortir et le faire revenir près des moteurs.
Nous pourrions contourner ce problème en faisant en sorte que les axes soient bien plus grand que la zone de travail. Mais:- Cela impliquerait un ajout de matière, et donc de masse
- Cela n'empêcherait pas un utilisateur au joystick de bloquer le robot
- Il s'agit d'une idée très complète. Cependant, lorsque l'effecteur se trouve à l'extrémité des deux axes de guidage, il faut exercer une force massive pour l'en sortir et le faire revenir près des moteurs.
- Robot type SCARA
- Il s'agit de notre idée de départ de base, mais à la découverte de l'idée numéro 6 qui nous permettra de déplacer les deux moteur sur le corps de la base du robot, on a décidé de développer le robot type parallélépipède.
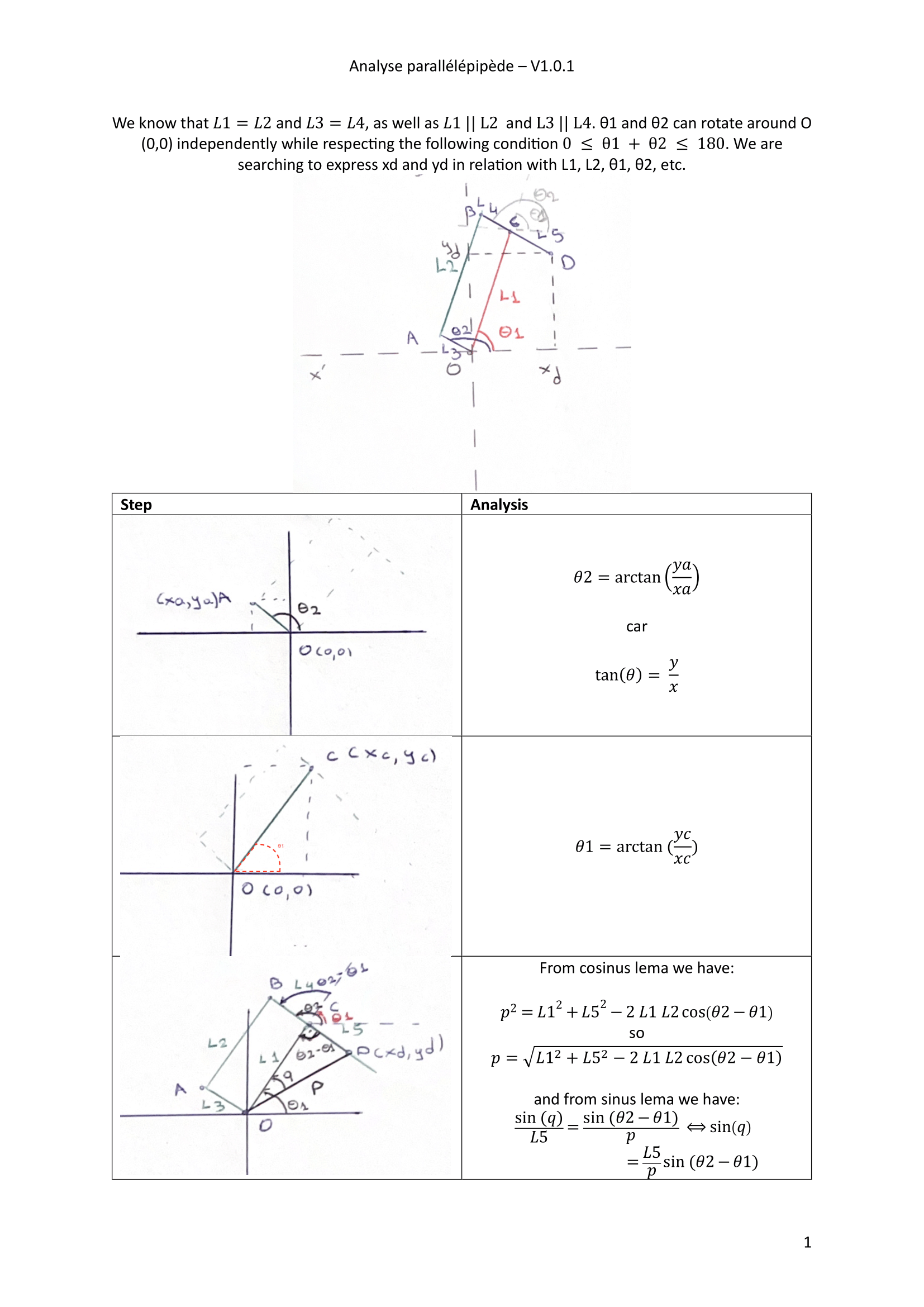
Étape 2: Conception détaillée
Modèle géométrique
Nota bene
On avait déjà commencé l'analyse du modèle cinématique du robot de l'idée numéro 5 (type SCARA). Ci-dessous vous allez trouver l'option également de visualiser et voir le calcul qui était effectué pour ce robot, ainsi que pour le robot type parallélépipède (idée numéro 6).
Les équations trouvées dans le modèle parallélépipède étant impossible à résoudre, on se base d'abord sur celles du SCARA tout en adaptant ces-dernières aux spécificités de notre modèle
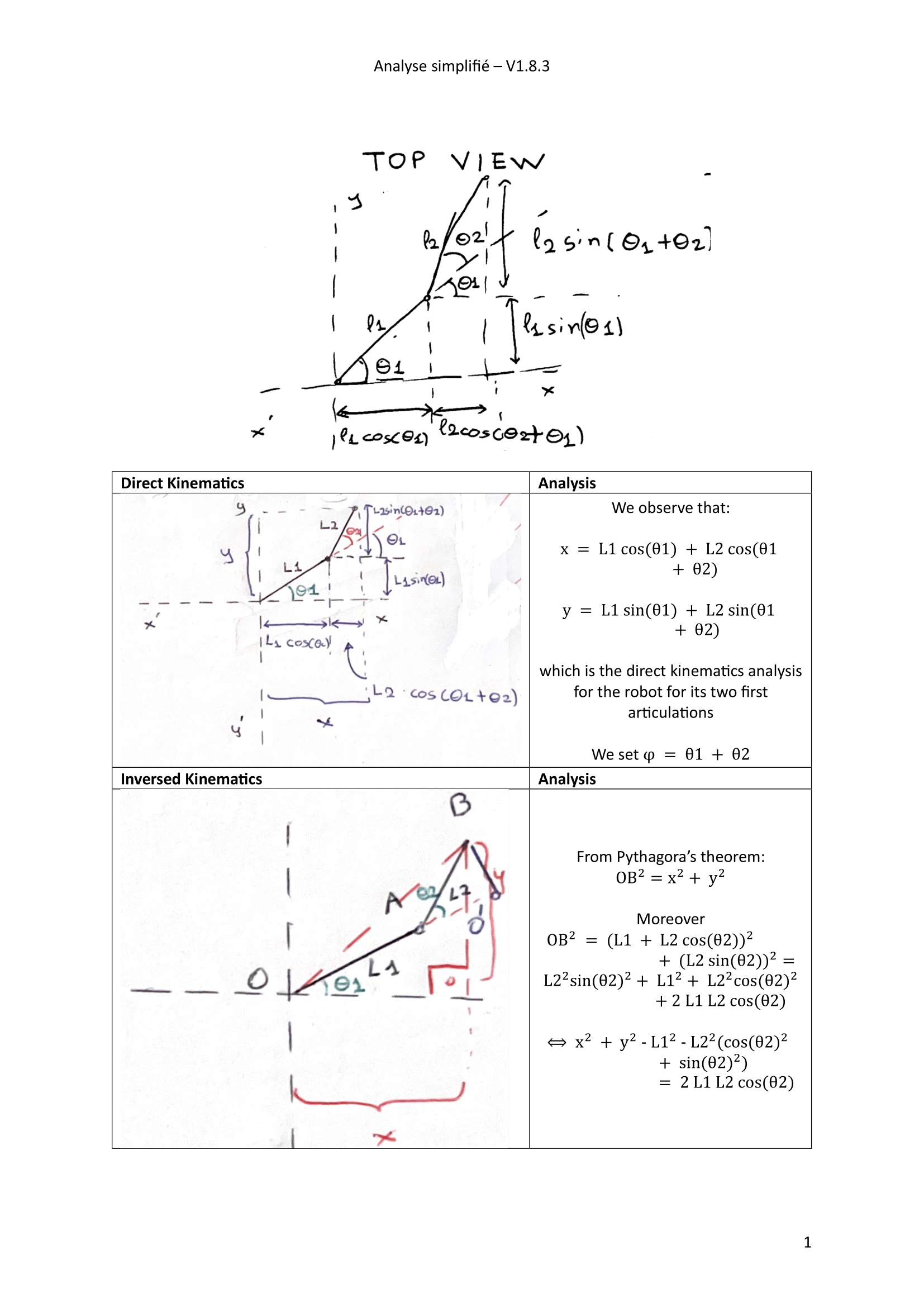
Robot type SCARA
Cinématique
Schéma Cinématique + Tableau DH
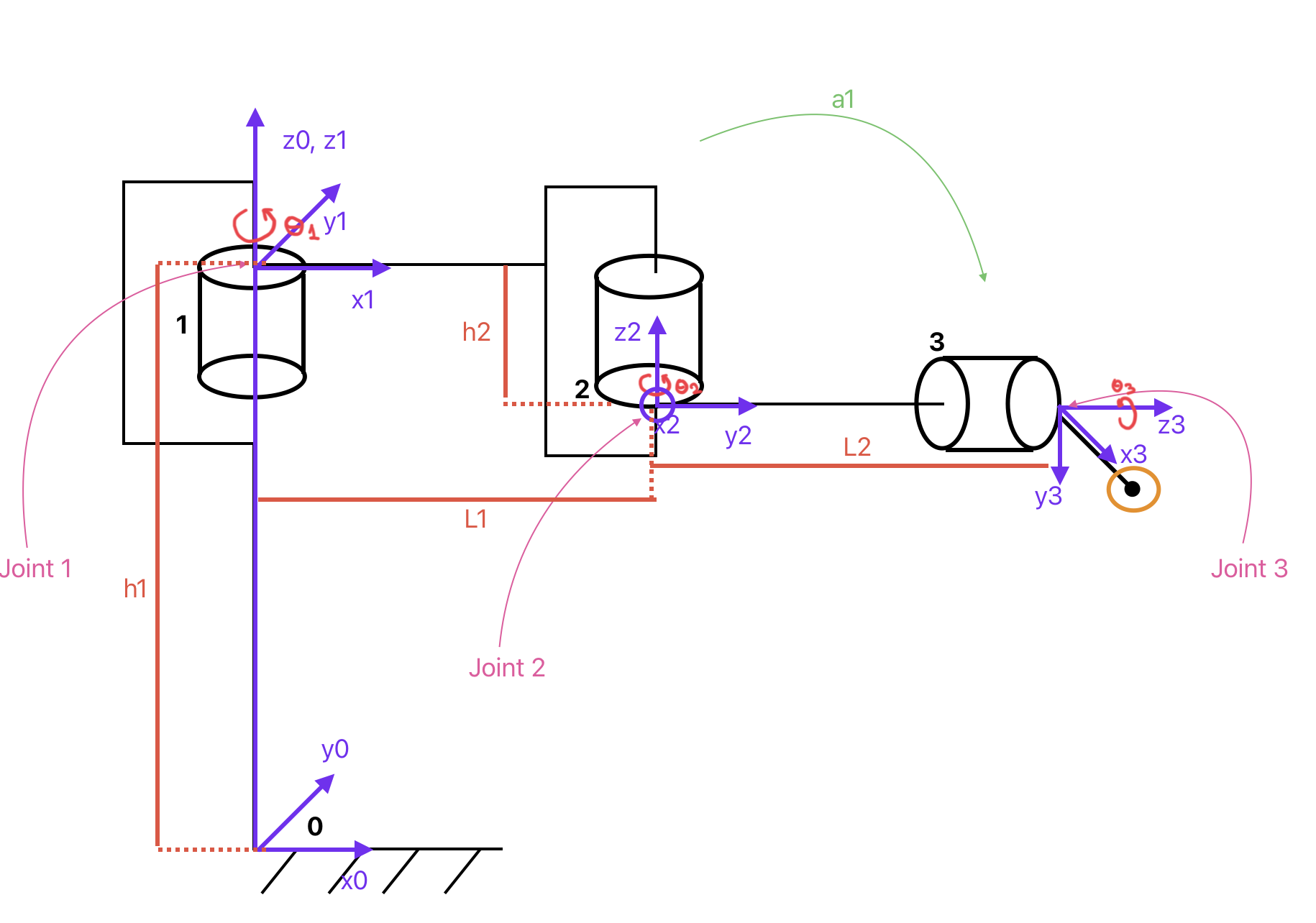 Les deux premières liaisons, pour 𝑖∈{1,..,2}, sont des liaisons pivot d’axe (𝑂𝑖,𝑧𝑖). La troisième liaison est une liaison pivot d'axe aussi selon z3.
Les deux premières liaisons, pour 𝑖∈{1,..,2}, sont des liaisons pivot d’axe (𝑂𝑖,𝑧𝑖). La troisième liaison est une liaison pivot d'axe aussi selon z3.
Modèle géométrique directe (complet)
Calculant T0->1, T1->2, T2->effector, ainsi que T0->effector.
Les résultas sont disponibles en PDF sur: Matrices de transformation homogene.pdf
Modèle géométrique directe (simplifié)
On peut aussi se concentrer uniquement sur les deux premières rotations car ce sont elles qui donneront la position finale du stylo. Après un moment donné pour écrire ou non, on peut configurer cela en programmation. De cette façon, nous pouvons simplifier le calcul comme ci-dessous :
Les résultats sont disponibles en PDF sur: SCARA Simplified Robot.pdf
Modèle géométrique inverse
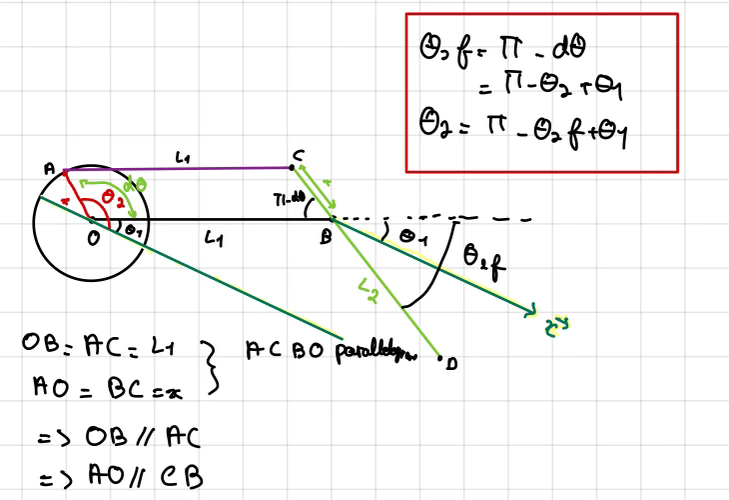
Ainsi selon le modèle géométrique directe et le la trigonométrie du systéme:
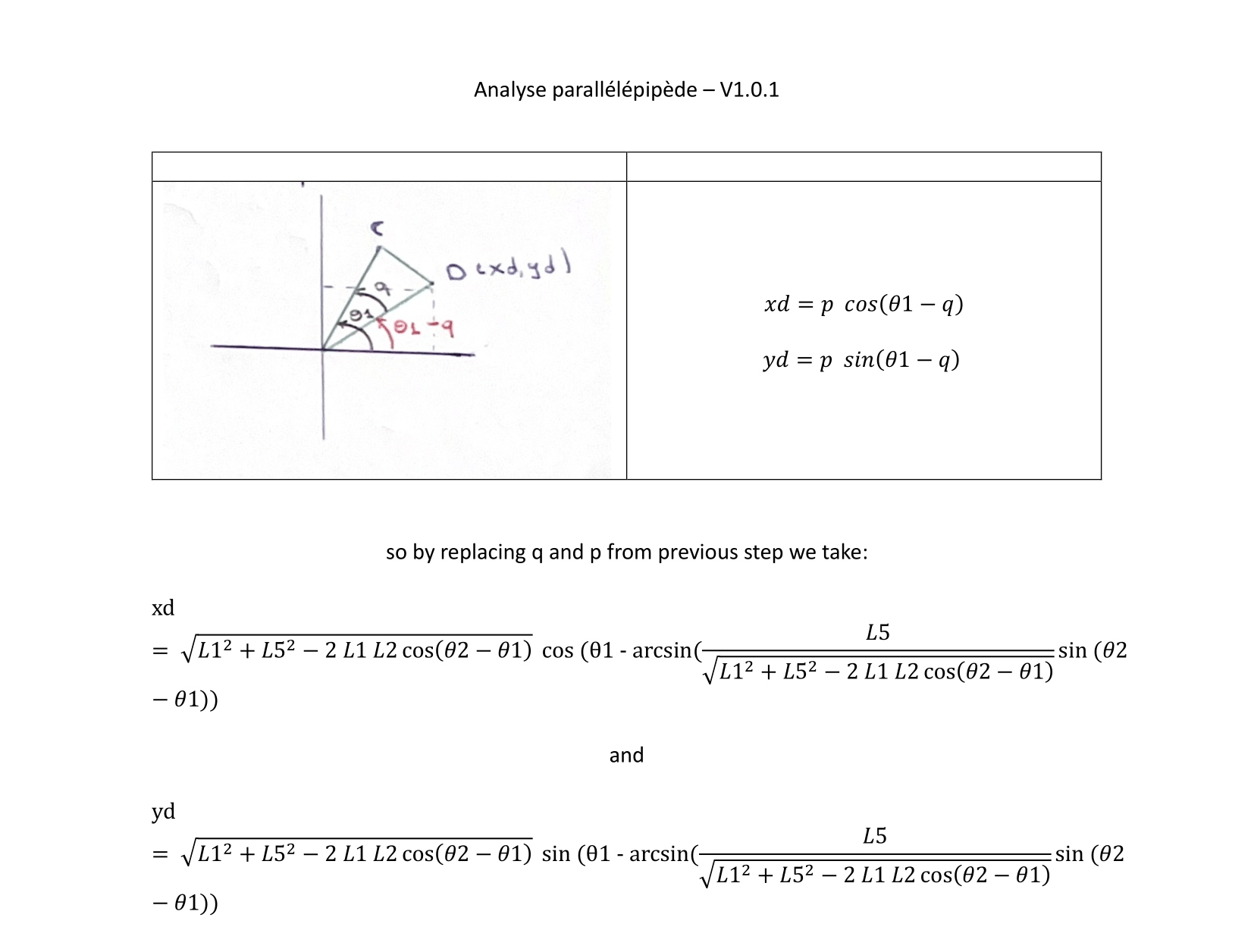
Robot type parallélépipède
Modèle géométrique directe
Ci-dessous, vous trouverez l'approche mathématique du robot type parallélépipède pour sa modèle géométrique directe.
Les résultats sont disponibles en PDF sur: Parallélépipède Robot.pdf
Spécifications de notre modéle
Avant trouver l'angle θ2 final, il faut procéder au choix de notre sens du plan, qui dépend de la configuration du robot et de l'angle θ1. Le calcul suivant nous permet d'obtenir la formule final de l'angle θ2:
Schéma électronique
Sur notre schéma électronique il y a un bouton qui permet de changer entre mode manuelle et mode automatique. De plus, il y a deux LED qui indiquent sur quel mode on est un moment donné. Par exemple si on est en mode manuelle, la LED bleue est allumée, sinon la LED verte est allumée. En outre, vous pouvez aussi trouver la connexion du joystick analogique dont on a besoin pour la réalisation de l'exercice 2. Il faut noter que le joystick à un fonctionnement de bouton intégré. On peut utiliser cette fonctionnalité pour contrôler plein de différentes choses, par exemple:
- Le stylo écrit ou pas.
- On fait un dessin avec le joystick qu'on visualise sur l'écran de l'ordinateur et on tape le bouton pour confirmer le dessin afin qu'il est créé par le robot.
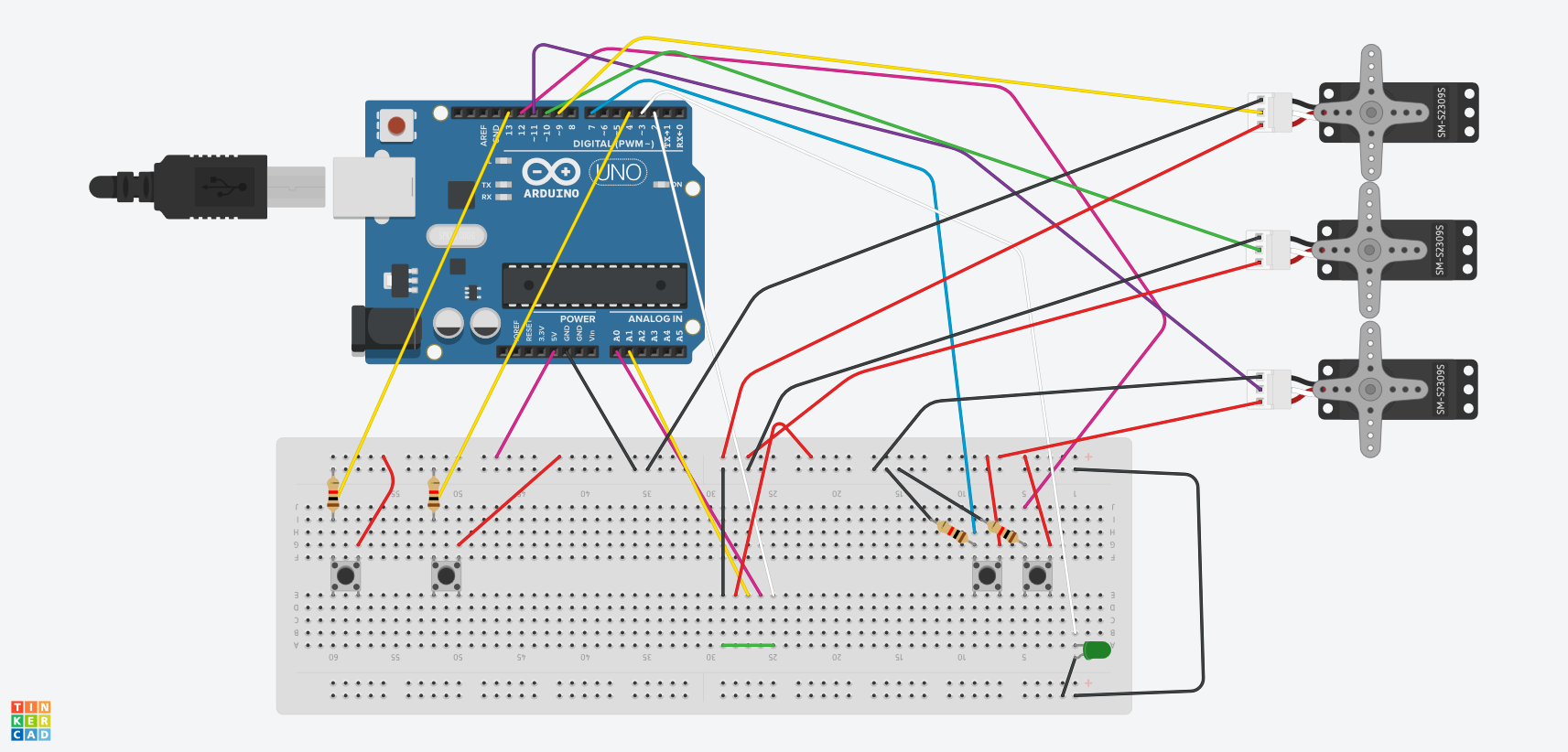 Figure 8: Schéma électronique V1.5.0
Figure 8: Schéma électronique V1.5.0
Modélisation
Notre objectif principal était de modéliser le robot selon un design à la fois compact et rigide. Un autre aspect important était de minimiser la quantité de matière utilisée et de réduire au maximum le temps de fabrication. Un modèle assemblé sur SolidWorks est disponible ci-dessous.
 Figure 9: Démonstration du mécanisme du robot LineaScribe
Figure 9: Démonstration du mécanisme du robot LineaScribe
Sous-assemblages
- Bâti support
- Articulations parallèles
- Pivot joint
- Pivot motor
- Axe d'effecteur
- Effecteur
Bâti support
C'est le corps principal du robot. Son objectif principal est de maintenir les deux moteurs sur le même axe de rotation. Il doit être capable de supporter les forces exercées par les moteurs vers les articulations parallèles ainsi que le retour des forces de frottement.
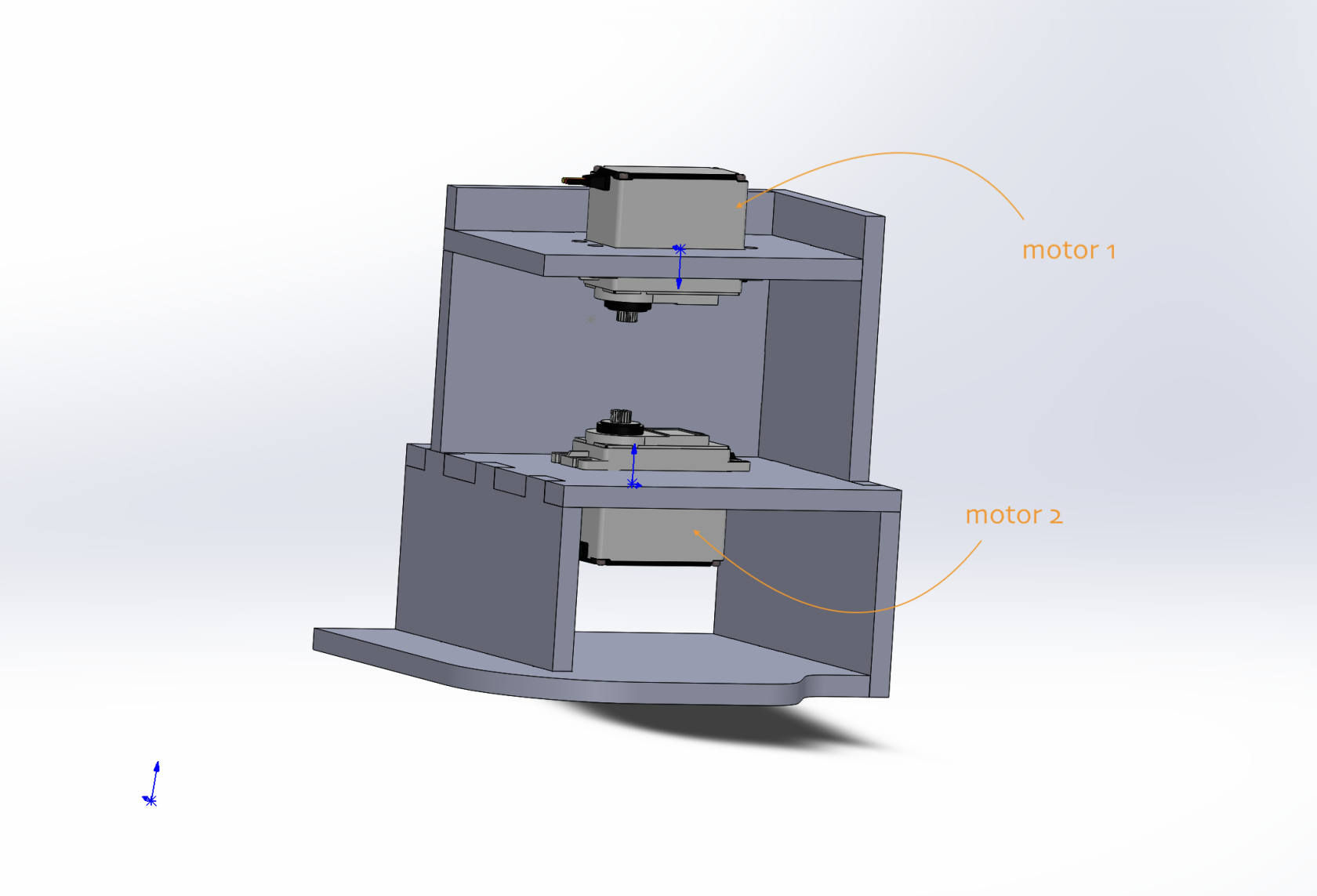 Figure 10: Bâti support du robot avec les moteur assemblés
Figure 10: Bâti support du robot avec les moteur assemblés
Le bâti est entièrement créé en utilisant la découpe laser. Concernant la conception de la pièce, il faut noter que le plan du moteur du haut (moteur 1) est conceptualisé de manière à ne pas permettre le détachement des pièces tout en acceptant un stress excessif par les articulations principales du robot.
Articulations parallèles (billettes)
Elles sont également entièrement conceptualisées pour la découpe laser (3 couches différentes de 3 mm). Elles sont montées sur les pièces "pivot joint" et "pivot motor" en utilisant des roulements 7201 BEGAP. Elles sont:
| Billette Principale | Billette Secondaire |
 |
 |
Pivot joint
Son rôle et la précision d'application sont essentiels pour le bon fonctionnement du robot. Il nous permet d'obtenir la distance correcte en parallélisme, comme indiqué dans le design ci-dessous. Il est entièrement créé en utilisant la découpe laser (2 couches de 3 mm).
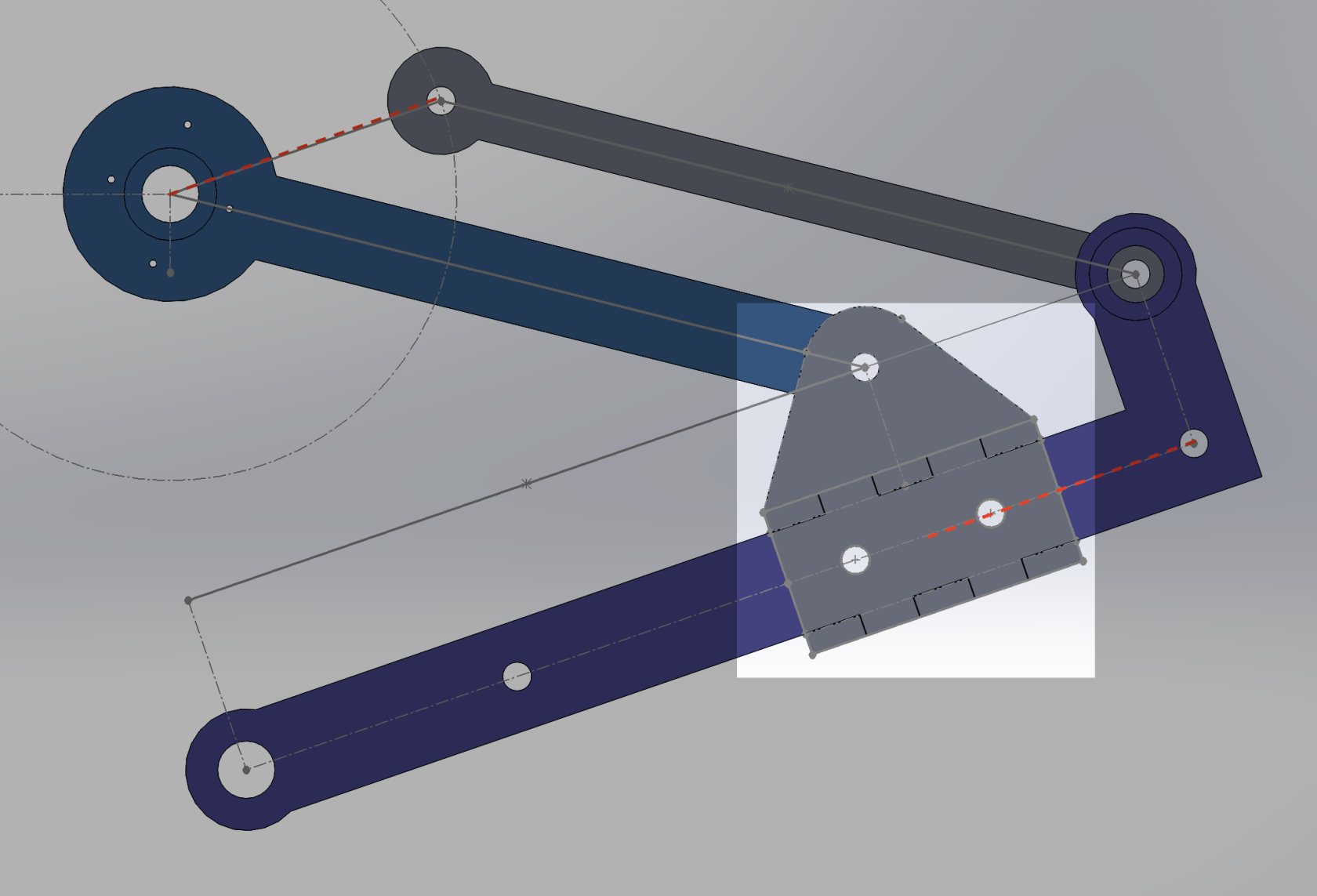 Figure 11: Focalisation sur la pièce "pivot joint"
Figure 11: Focalisation sur la pièce "pivot joint"
Pivot motor
C'est la seule pièce qui est modélisée pour l'impression 3D. Son rôle est le même que celui de la pièce "pivot joint". Elle est directement montée sur le moteur du bas (moteur 2). Pour renforcer la partie de la pièce qui recevra les forces de frottement du stylo, un triangle de renfort a été ajouté, comme vous pouvez le voir ci-dessous.
 Figure 12: Triangle de renfort de "pivot motor"
Figure 12: Triangle de renfort de "pivot motor"
L'axe centrique est un détail et il n'est pas requis pour le fonctionnement correct du mécanisme.
 |
 |
 |
Axe d'effecteur (billette Emax)
Il s'agit de l'axe qui supporte l'outil de l'effecteur. Il est guidé par les axes parallèles et mis en position (MIP) par la pièce "pivot joint". Le moteur est mis en position grâce à "Pignon Servo Emax". C'est la plateforme sur laquelle on fixe le moteur Emax comme on peut observer ci-dessous :
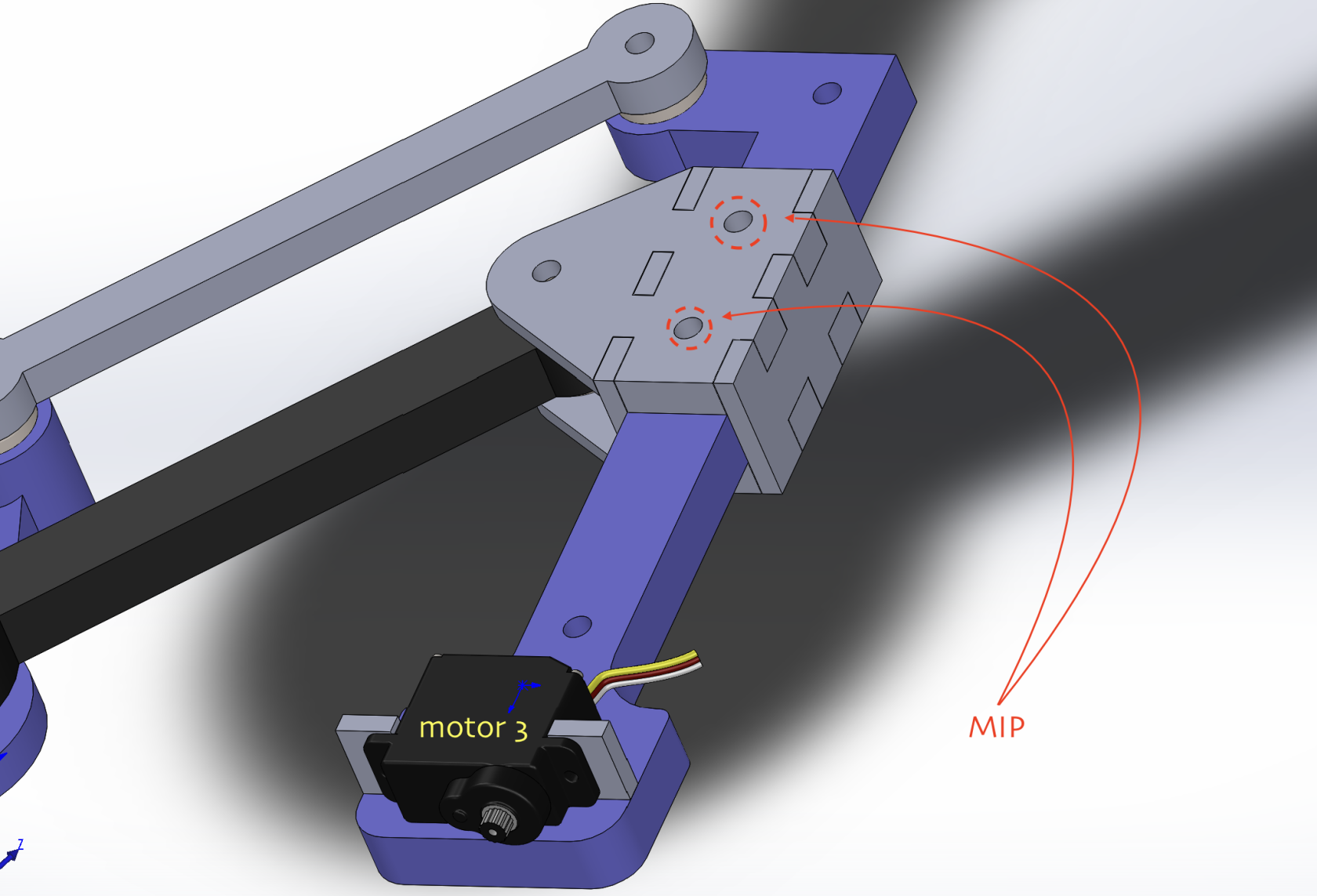 Figure 13: Billette Emax en assemblage avec le moteur 3 (Emax)
Figure 13: Billette Emax en assemblage avec le moteur 3 (Emax)
 Figure 14: Modèle d'un pignon servo Emax
Figure 14: Modèle d'un pignon servo Emax
Effecteur
L'outil de l'effecteur est l'élément terminal du robot qui entre en contact direct avec la surface d'écriture. Son rôle principal est de tracer des lignes en utilisant un stylo. Voici la deuxième pièce en impression 3D :
 Figure 15: La pièce qui va soutenir l'outil (le stylo dans notre cas)
Figure 15: La pièce qui va soutenir l'outil (le stylo dans notre cas)
Solidworks
Tous les fichiers et les fichiers d'assemblage sont disponibles sur: LineaScribe Robot.zip. Voici l'organisation des fichiers :
- Architecture : il s'agit d'un fichier squelette des différentes configurations. Si vous changez les dimensions des pièces présentes dans ce squelette, elles sont mises à jour dans tous les assemblages.
- Assemblage bras > Pièce Liaison Billette Principale - Billette Emax : C'est notre "pivot joint"
- Assemblage bras > ActionneurServo : C'est notre "motor joint"
- Assemblage bras > Billette * : ils sont les différents billettes du robot
- Assemblage bras > Pignon servo max : c'est pour la mise en position du moteur Emax commet on peut voir à la figure
- Assemblage bras > Liaison axe : il s'agit de l'assemblage complet du mécanisme qui va se visser sur les actionneurs.
- Assemblage > Assemblage1 : il s'agit de l'assemblage total du robot.
- Assemblage bras > Effecteur : C'est notre "effecteur"
Fichiers SVG & STL
- batis.svg (MDF 6mm)
- pivot joint.svg (MDF 3mm)
- bilette1.svg - articulation parallèle 1 - billette principale (MDF 3mm)
- bilette2.svg - articulation parallèle 2 - billette secondaire (MDF 3mm)
- pivot motor.STL (3D Maker PLA 30% infill - no support)
- bilette3 et pignon EMAX.svg (MDF 3mm)
- Effecteur.STL (PLA 1.75mm)
Modèle géométrique inverse: vérification
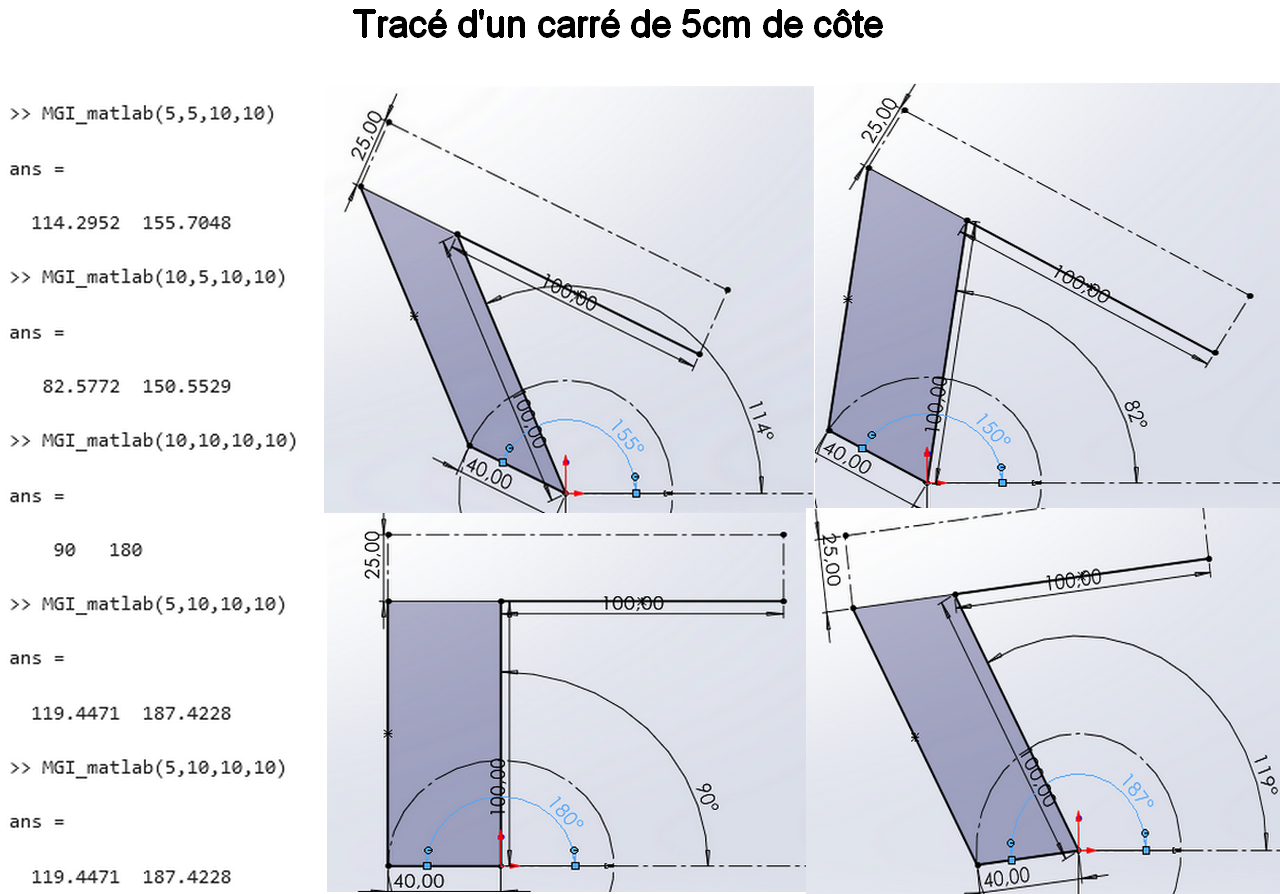
D'après le calcul des robots de type parallélépipède et SCARA, nous avons développé un script sur MATLAB permettant de vérifier le calcul des coordonnées du plan cartésien x, y en fonction des angles θ1 et θ2.
Notre analyse a permis de conclure que :
- Dans le cadre de la limitation de l'espace d'écriture de la plateforme, il existe parfois plusieurs solutions possibles pour atteindre une position spécifique. Il ne s'agit pas de singularités, mais plutôt de libertés de rotation autour des axes des moteurs. Cependant, le robot ne peut pas se placer à certains endroits en raison de la modélisation (support du moteur 1).
- Il est donc nécessaire de trouver une procédure permettant de choisir la solution du système qui est acceptable.
Voici le fichier MATLAB: MGI_matlab.m
Pour utiliser le fichier il suffit d'appeler la fonction MGI_matlab, et passer comme arguments les coordonnées x, y et L1 et L2 les longueurs des articulations du robot. On a ci-dessous le résultat lorsqu'on exécute la fonction pour obtenir les 4 sommets d'un carré (5cm) et qu'on entre les angles renvoyés dans notre esquisse du bras.
Pistes de programmation
Organigramme:
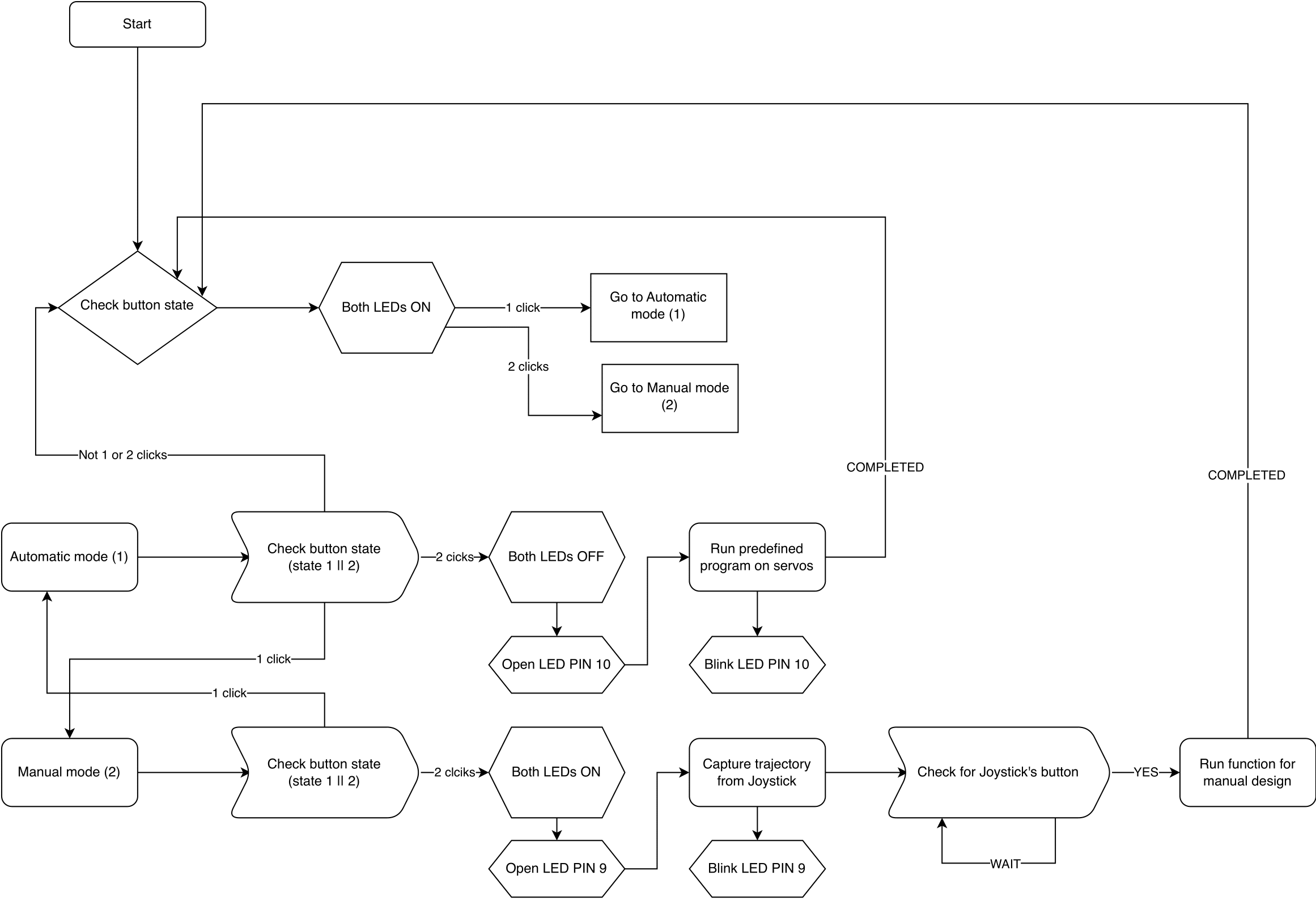 Figure 16: Pistes de programmation version 1.0.0
Figure 16: Pistes de programmation version 1.0.0
Document PDF V1.0.0: FlowChart.pdf
Programmation
Application du modele géométrique inverse pour calculer les angles de control de moteurs
/* Takes a cartesien position (x,y) and updates the angles teta1 and teta2 that control the two motors (located on the same r) */
void get_angles(double x, double y, float L1, float L2, double* teta1, double* teta2){
//Distance between the center of the robot and the starting point of the writing area
x+=dx;
y+=dy;
//Geometric inveresed model available under teh section "Robot type SCARA"
co2 = (x*x+y*y-L1*L1-L2*L2)/(2*L1*L2);
teta2prec = atan2((-sqrt(1-co2*co2)),co2); //The root decides the orientation according to the configuration
//Calculating the angle 1
*teta1 = atan2(y,x) - atan2((L2*sin(teta2prec)),(L1+L2*cos(teta2prec)));
teta2prec = teta2prec*180/pi; //rad to degrees
*teta1 = *teta1*180/pi;
*teta2 = *teta2*180/pi;
//teta2 is the final corrected angle according to "Specifications de notre modele" available on the Robot's documentation -> voir wiki
*teta2=-abs(teta2prec)+*teta1+180;
*teta2 = 180-*teta2;
}Control du stylo
/* Controls the tool's position [choose between UP and DOWN] */
void pen_control(int control, int *penstate) //Down, up, swithc state
{
if (control == DOWN) //write with pen [pen is down]
{
servo3.writeMicroseconds(pen_down);
*penstate=0;
}
if (control == DOWN_) //write with pen [pen is down]
{
servo3.writeMicroseconds(pen_down_);
*penstate=0;
}
else if (control == UP) //disable writing [pen is up]
{
*penstate=1;
servo3.writeMicroseconds(pen_up);
}
else if (control == UP_) //disable writing [pen is up]
{
*penstate=1;
servo3.writeMicroseconds(pen_up_);
}
else if (control == SWITCH) //disable writing [pen is up]
{
switch(*penstate){
case 0:
servo3.writeMicroseconds(pen_up);
*penstate=1;
break;
case 1:
servo3.writeMicroseconds(pen_down);
*penstate=0;
break;
}
}
else
{
printf("An error occured on controling the pen\n");
}
}
Designer une ligne
/* Draws a straight line in a specific length and to a given angle */
void straight_line(double *x_start, double *y_start, float length, double angle)
{
//Note: We divide the distance in multiple subpoints to be acquired. The greater the number, the most precision we can achieve of course with some limitations
for (double i = 0; i < length*900; i++)
{
*x_start = *x_start + cos(angle)/900; //Current position + shift
*y_start = *y_start + sin(angle)/900;
get_angles(*x_start,*y_start,L1,L2,&teta1, &teta2); //calculation of motors' angles
servo1.write(teta1); //Sending data to the motors
servo2.write(teta2);
delay(1);
}
}Designer un
#include/* <Servo.h>Designing consta circle in a specific radius and a specific starting point */
void circle(double x_center, double y_center, double angle_start, double angle, double radius, double *x, double *y, int buttonPininit, int res)
{
//Placement in a specific starting point
if(init==0){
*x = 8;x_center const+ (radius * cos(radians(angle_start)));
*y = y_center + (radius * sin(radians(angle_start)));
get_angles(*x,*y,L1,L2,&teta1, &teta2);
servo1.write(teta1);
servo2.write(teta2);
delay(1000);
//Get into writing position
pen_control(DOWN,&penstate);
delay(500);
}
//Repetead calculation different points between a starting angle and a final angle
for (double i = (angle_start*res); i < (angle*res); i++)
{
*x = x_center + (radius * cos(radians(i/res))); //Formula of finding the position of a point is based on the tan function decomposed in x and y axis
*y = y_center + (radius * sin(radians(i/res)));
get_angles(*x,*y,L1,L2,&teta1, &teta2); //Calculation of angles for the motors
servo1.write(teta1); //Sending data to the motors
servo2.write(teta2);
delay(1);
}
}Designer un circle en pointilles
/* Designs a dotted circle in a specific radius and a specific starting point */
void dotted_circle(double x_center, double y_center, double angle_space, double angle_dot, double radius, double *x, double *y)
{
*x = x_center + (radius * cos(radians(0)));
*y = y_center + (radius * sin(radians(0)));
get_angles(*x,*y,L1,L2,&teta1, &teta2);
servo1.write(teta1);
servo2.write(teta2);
delay(1000);
//It's a recursive loop leading to a 360 degrees circle that calls circle function with a starting and final point
double i=0.0;
while(i < 360) {
pen_control(DOWN_, &penstate);
delay(200);
circle(x_center, y_center,i, angle_dot+i, radius, x, y, 1, 10);
delay(200);
i = i + angle_dot; //update of the current position - required to verify of a circle of 360 degress has been designed
if(i>=360) break;
//Between delays we chage writing mode in order to create a dotted effect
pen_control(UP, &penstate);
delay(200);
circle(x_center, y_center,i, (angle_space+i), radius, x, y, 1, 10);
i = i + angle_space;
delay(200);
}
}Designer un carre
/* Designs a square of a given length and in a given angle */
void square(double *x, double *y, int ledAutoPin = 10;
constlength, int ledManualPinangle)
={
9;//Square constis composed of four straight lines of a given length and they are vertical between them
straight_line(x,y,length, radians(angle));
delay(1000);
straight_line(x,y,length, radians(angle+90));
delay(1000);
straight_line(x,y,length, radians(angle+180));
delay(1000);
straight_line(x,y,length, radians(angle+270));
delay(1000);
}Logic du Joystic
/* Logig for joystick manipulation */
void Joystick(double *x, double *y)
{
int servo1Pin = 6;
const int servo2Pin = 5;
const int servo3Pin = 3;
const int joystickButtonPin = 7;
const int verticalJoystickPin = A1;
const int horizontalJoystickPin = A0;
Servo servo1;
Servo servo2;
Servo servo3;
int buttonState = dimx=0;
int previousButtonStatet=0;
=//Sending mode on, sending joystick data to processing
int out=0;
int clickCountout1=0;
while(out==0){
//We check if we read the values of the Joystick where the user decided to stop (On verifie si on Lit les valeurs du Joystick ou l'utilisateur a decide d'arrete)
if (Serial.available() > 0) {
String response = 0;Serial.readStringUntil('\n');
int currentState = 0;
int trajectoryPoints[100][2]response.trim(); // ArrayRemove toany storeleading trajectoryor pointstrailing intwhitespace
trajectoryIndexif = 0;
void setup((response.equals("Done")) {
pinMode(buttonPin, INPUT_PULLUP)//digitalWrite(13,LOW);
pinMode(ledAutoPin,break; OUTPUT);// pinMode(ledManualPin,Stop OUTPUT);sending pinMode(joystickButtonPin,data INPUT_PULLUP);to servo1.attach(servo1Pin);
servo2.attach(servo2Pin);
servo3.attach(servo3Pin);processing
}
void}
loop(//Reading Joysticks values
xtemp = analogRead(pinx);
ytemp = analogRead(piny);
buttonval1 = 1-digitalRead(pinbutton1);
buttonval2 = digitalRead(pinbutton2);
//Sending Joysticks values to processing
Serial.print(xtemp);
Serial.print("\t");
Serial.print(ytemp);
Serial.print("\t");
Serial.print(buttonval1);
Serial.print("\t");
Serial.println(buttonval2);
//This loop prevents the overlap of several values given that the frequency of sending data from the Arduino is higher than the frequency of receiving processing (Cette boucle empeche le chevauchement de plusieur valeur etant donne que la frequence d';envoi de donne de l'arduino est plus eleve que la frequence de recoit de processing)
//We therefore wait until the data is read by processing before sending another data (On attend donc jusqu'a ce que la donnee est bien lu par processing avant d'envoyer une autre donne)
out1=0;
while (out1 == 0) {
checkButton()//digitalWrite(13,LOW);
if (clickCountSerial.available() > 0) {
String response == 1)Serial.readStringUntil('\n');
{response.trim(); // ChangeRemove stateany onleading singleor presstrailing currentStatewhitespace
=if (currentStateresponse.equals("Done")) =={
1) ? 2 : out=1; clickCount//get =out 0;of the loop //checck andif we really get out of the loop check if it doesnt give another line of data after i wanted to start
out1=1;
}
else if (clickCountresponse.equals("Received")) == 2) {out1=1; // ExecuteExit currentwhile state on double press
clickCount = 0;
if (currentState == 1) {
runAutomaticProgram();
blinkLED(ledAutoPin);
} else if (currentState == 2) {
if (digitalRead(joystickButtonPin) == LOW) {
executeTrajectory();
blinkLED(ledManualPin);loop
}
}
}
//tab Lightdata
bothdouble*** LEDstab;
//Receive tab dimensions
while waiting for a state selection
digitalWrite(ledAutoPin, HIGH);
digitalWrite(ledManualPin, HIGH);
}
void checkButton()(true) {
buttonStateif (Serial.available() > 0) {
String receivedString = digitalRead(buttonPin)Serial.readStringUntil('\n'); // Read until newline character
//decode data
int rowIndex = 0;
int colIndex = 0;
int depthIndex = 0;
String buffer = ""; // Buffer to hold the float string
//premier element
int i = 0;
while(1){
char c = receivedString.charAt(i);
if (buttonState != previousButtonState && buttonStatec == LOW)',') {
clickCount+dimx = buffer.toInt();
buffer = ""; // Reset buffer
}
else if (c == ';') {
t = buffer.toInt();
buffer = ""; // Reset buffer
i++;
break;
}
else {
buffer += c; // Add character to buffer
}
i++;
}
previousButtonStateif(t==1) digitalWrite(ledPin, LOW);
tab = buttonState;(double ***)malloc(t * sizeof(double **));
for (int l = 0; l < t; l++) {
tab[l] = malloc(2 * sizeof(double*)); //tableau de donne
for (int j = 0; j < 2; j++) {
tab[l][j] = malloc(dimx * sizeof(double));
}
}
for (i; i < receivedString.length(); i++) {
char c = receivedString.charAt(i);
if (c == ',') {
tab[depthIndex][rowIndex][colIndex] = buffer.toDouble();
colIndex++;
buffer = ""; // TurnReset off LEDs after button press is detected
digitalWrite(ledAutoPin, LOW);
digitalWrite(ledManualPin, LOW);buffer
} voidelse runAutomaticProgram(if (c == ';') {
//tab[depthIndex][rowIndex][colIndex] Your= codebuffer.toDouble();
torowIndex++;
movecolIndex the= servos0;
inbuffer a= predefined way""; // Example:Reset buffer
} else if (c == '|') {
tab[depthIndex][rowIndex][colIndex] = buffer.toDouble();
depthIndex++;
rowIndex = 0;
colIndex = 0;
buffer = ""; // Reset buffer
} else {
buffer += c; // Add character to buffer
}
}
// Capture the last float value
tab[depthIndex][rowIndex][colIndex] = buffer.toDouble();
break;
}
}
for (int j = 0; j < t; j++) {
get_angles(tab[j][0][0],tab[j][1][0],L1,L2,&teta1, &teta2); //Position initiale
servo1.write(teta1);
servo2.write(teta2);
delay(1000);
pen_control(DOWN,&penstate);
delay(500);
for (int i = 0; i < 10;dimx; i++) {
double xt = tab[j][0][i];
double yt = tab[j][1][i];
if(xt!=-1 && yt!=-1){
get_angles(xt,yt,L1,L2,&teta1, &teta2);
servo1.write(i * 10)teta1);
servo2.write(90 - i * 5);
servo3.write(180 - i * 15);
delay(500);
}
}
void captureTrajectory() {
trajectoryPoints[trajectoryIndex][0] = analogRead(verticalJoystickPin);
trajectoryPoints[trajectoryIndex][1] = analogRead(horizontalJoystickPin);
trajectoryIndex++;
if (trajectoryIndex >= 100) {
trajectoryIndex = 0;
}
}
void executeTrajectory() {
for (int i = 0; i < 100; i++) {
// Use trajectoryPoints[i][0] and trajectoryPoints[i][1] to move servos
// Example:
servo1.write(trajectoryPoints[i][0]);
servo2.write(trajectoryPoints[i][1]);
servo3.write(map(trajectoryPoints[i][1], 0, 1023, 0, 180))teta2);
delay(100);
}
}
void blinkLED(int ledPin) {
for (int i = 0; i < 5; i++) {
digitalWrite(ledPin, HIGH)pen_control(UP,&penstate);
delay(100)500);
}
}
Journal de bord / Calendrier
Avancée du projet à chaque étape, difficultés rencontrées, modifications et adaptations
14/02/2024
Discussion autour du Projet Robotique ROB3 - différents idées, décision, planning.
16/02/2024
Création du schéma cinématique, de la table DH. Etablissement d'un premier modèle géométrique
19/02/2024
Finalisation du dossier de conception préliminaire. Mise a jour du modèle géométrique et de la table DH, création du modèle géométrique inverse
22/02/2024
Début de modélisation des pièces du robot
24/02/2024
Recherche sur les méthodes de géométrie inverse du robot
02/03/2024
Finalisation de la partie modèle géométrique directe et inverse
08/03/2024
Impression des pièces du bâti support et on a lancé l'impression 3D du "pivot motor"
24/04/2024
Programmation des fonctions lignes et carré (pour tests) et connexion au joystick.
25/04/2024
Début de la fonction joystick. Assemblage et câblage définitif du robot. Programmation du cercle pour l'exercice 1
22/05/2024
Finalisation du joystick. Programmation de la fonction pointillés
23/05/2024
Tests finaux et présentation.