LU3SV564 : impact des vibrations du métro parisien sur le développement des plantes

Informations

• Jolhan Perrin, Gaspard Rollin, Violette Noël, Shan-ning Phillipot
• jolhan.perrinpro@gmail.com, 
• L3 Sciences de la Vie - Projet d'UE - Démarche scientifique en Écologie urbaine (LU3SV564)
• Septembre 2025 - Décembre 2025

Contexte

[INTRODUCTION] 

Objectifs

Nulla imperdiet mattis neque non vehicula. Aliquam aliquam ac lectus non euismod. Nulla facilisi. Fusce fermentum enim magna, vel consectetur sem malesuada eu. Integer ac iaculis magna, dictum posuere neque. Sed pretium dignissim arcu, vel maximus felis cursus in.

Ajouter au moins une image de votre projet

----

Construction du générateur de vibrations 

Pour toute personne débutant en Arduino, comme nous l’avons été, n’hésitez surtout pas à regarder des vidéos et à vous aider de l'intelligence artificielle, surtout pour la programmation. Si vous utilisez une pièce électronique particulière, regardez sur Google sa “datasheet”, cela vous aidera énormément à comprendre ou brancher quoi. 

Afin de reproduire artificiellement les fréquences vibratoires émises par les métros parisiens, nous avons décidé d’utiliser un programme Arduino. Ceci nous permet de facilement contrôler les vibrations de manière à reproduire les heures de passage des métros et leur durée de “ressenti” sur un point fixe; le tout pour un coût relativement bas. 

La programmation Arduino devait aussi servir à programmer un capteur de vibration, sur la base du projet Sismomètre Vibrasense. Nous devions programmer l’arduino de manière à n’utiliser qu’un seul capteur Vibrasense (l’Axe Z), mais ceci a été abandonné car le capteur n’était pas assez précis. Il reste cependant efficace pour détecter une vibration. 

Nous avons tout d’abord commencé par suivre un cours d’initiation à l’arduino, afin de comprendre le fonctionnement de la carte Arduino UNO, les fondamentaux sur les branchements et sa programmation sur le logiciel Arduino IDE. 

Ensuite, nous avons commandé 8 shakers (des hauts-parleurs sans membrane) Monacor AR30, sur la base d’un article similaire à notre projet (https://doi.org/10.3390/acoustics7030045) 

L’arduino UNO seul n’apporte pas suffisamment de puissance pour faire fonctionner les 8 shakers. Il ne permet pas non plus de tous les connecter. Nous avons donc décidé d’utiliser une puce LM386 qui est un amplificateur sonore, accompagnée d’une alimentation 12 V-3 A. 

Nous avons utilisé un oscilloscope et un générateur de fréquence, avant d’utiliser l’arduino, pour visualiser la fréquence que l’on souhaitait programmer et vérifier si l’application Phyphox du téléphone reconnaissait correctement la fréquence produite par le générateur. 

Nous devons avant tout connaître la puissance nécessaire pour faire fonctionner correctement les shakers : 

P = Ri^2

i = sqrt(P/R) = sqrt(15/8) ≈ 1,4A (15 car 15W et 8 car 8 Ohm pour un shaker) 

U = Ri = 11V 

Même si cela est valable pour un seul shaker, nous nous sommes rendu compte qu’une seule alimentation suffisait (sûrement du fait qu’une simple fréquence ne demande que très peu de puissance). Chaque shaker branché n’ajoutait pas 1,4A

Il nous était toutefois nécessaire d’utiliser l’arduino et non le générateur car ce dernier ne nous permet que de produire une fréquence sans arrêt. De plus, nous souhaitons générer plusieurs fréquences en même temps, ce que le générateur ne peut pas faire (nous utiliserons in fine qu’une seule fréquence, expliquée plus bas). 

Avec l’arduino et la puce LM386, le branchement pour un seul shaker était le suivant : 

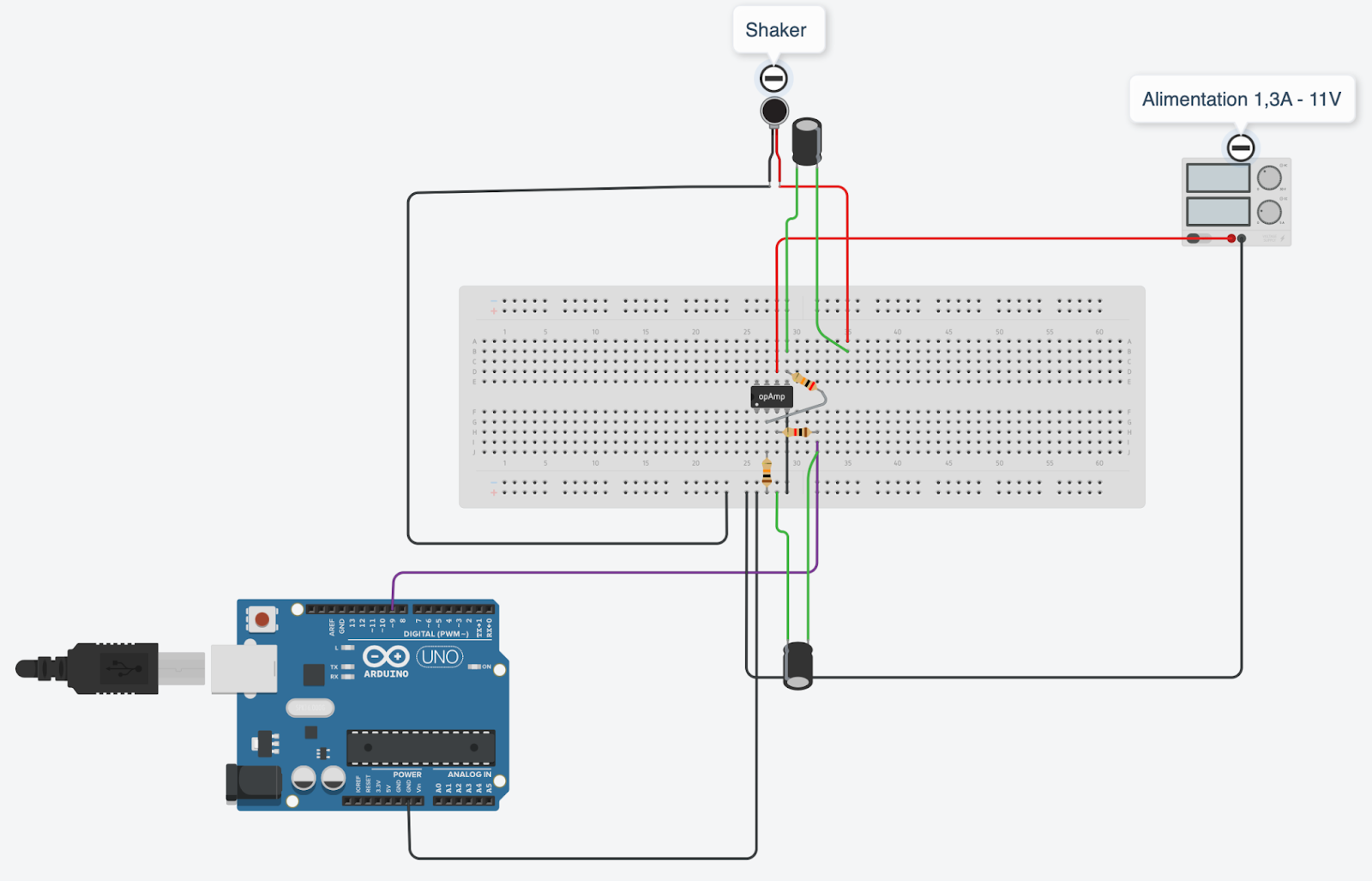
Nous avons utilisé un condensateur d'entrée de 0,25uF et un condensateur de sortie de 225uF (pourquoi ces valeurs ?), une résistance de 10KΩ sur l’entrée + du LM386, une résistance de 20KΩ la broche de sortie du LM386, et une résistance de 1,8KΩ à l’entrée - du LM386 ( pourquoi je ne sais pas non plus, il y a une histoire de R2 divisé par R1,mais c’est tout ce que je sais) 

Bien que fonctionnelle, la puce s’est mise à court-circuiter. Nous avons effectué plusieurs changements de branchement, notamment l’ajout de condensateur,  afin d’apporter un pic de fréquence plus “jolie” sur Phyphox, mais, nous supposons surtout que le problème venait du fait que la puce ne pouvait dégager que 1W de puissance max. Il tournait donc constamment à plein régime, ce qui l'a probablement fait cramer. 

Entre-temps, nous avions commandé des moteurs Driver L298N, qui ne semblaient pas le plus optimal pour l’amplification de son; là où  le LM386 est son principal objectif. Mais face au manque de temps et de budget, nous nous sommes rabattus sur ceux-là, pouvant accepter plus de puissance (15-25 W). Nous avions en tout 4 L298N, 1 pour 2 shakers. (le passage d’un métro n’est pas sinusoïdal, donc cela nous arrange en quelque sorte que la fréquence émise ne soit pas parfaite).

Voici donc le branchement pour 2 shakers. Nous avons utilisé un arduino pour 4 shakers, soit pour 2 L298N, soit pour 1 plaque :

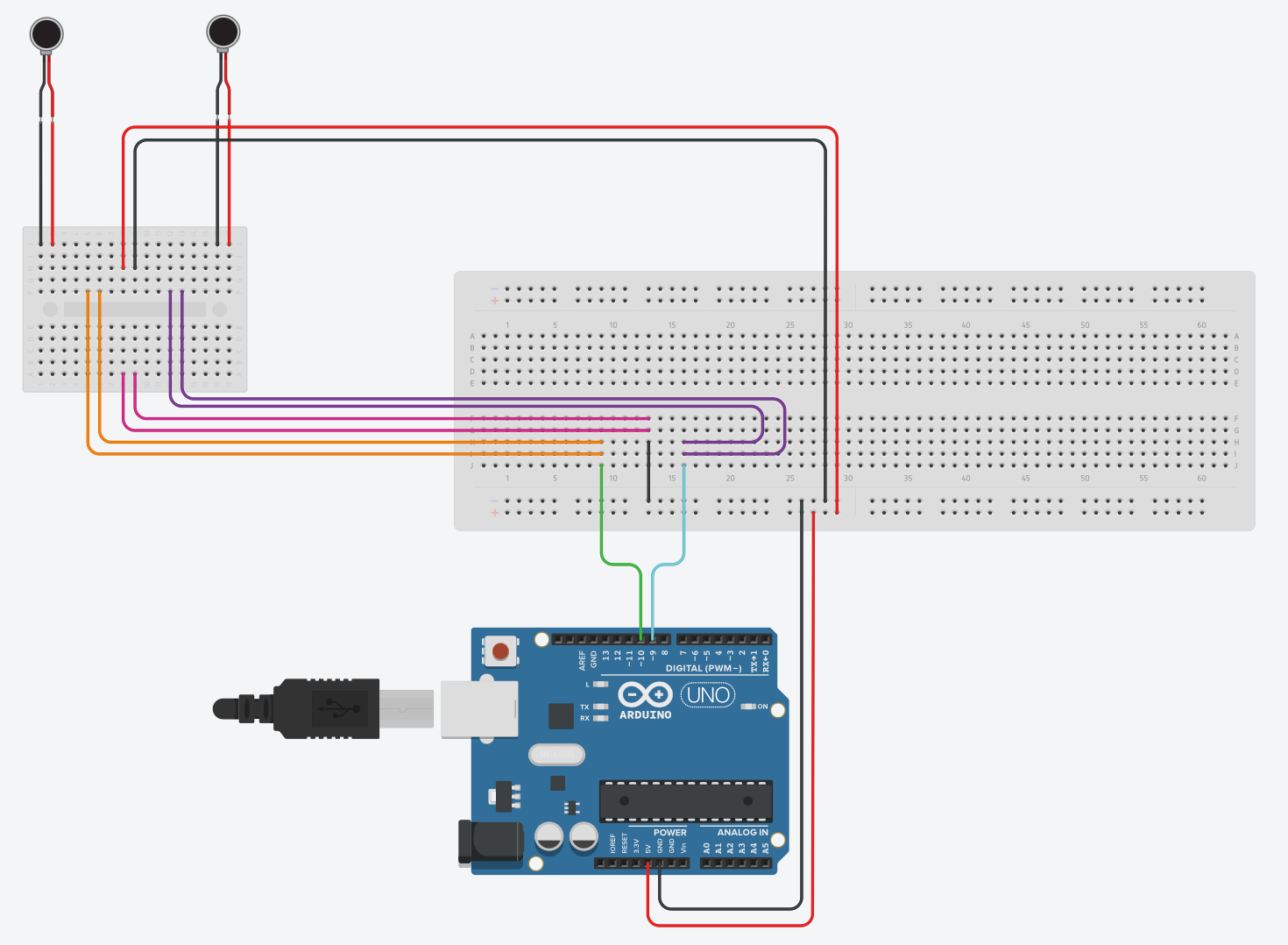
Info complémentaire à la compréhension du montage 

Le logiciel tinkercad ne permet pas d’ajouter le module L298N, il est représenté ici par la petite breadboard, à gauche. Les branchement dessus sont les suivants (se référer à la datasheet): 

• Shaker 1 sur OUT1 et OUT2 (peu importe le câble)

• Shaker 2 sur OUT3 et OUT4 (peu importe le câble)

• Câble rouge sur 5V (pas celui du shaker !)

• Câble noir sur GND (pas celui du shaker !)

• Câbles oranges sur IN1 et IN3

• Câbles violets sur IN2 et IN4 

• Câbles rôses sur ENA et ENB

Les broches 9 et 10 de l’arduino ne sont pas choisies au hasard : ce sont des broches PWM qui permettent de simuler une onde analogique (via un (cos) dans le programme), au lieu d'être bloquées à 'pleine puissance ON' ou 'pleine puissance OFF'.On essaye de reproduire au mieux une onde sinusoïdale, il nous faut donc un signal normal et son exact opposé (d’où l’utilisation de 2 broches). Le souci est que ce hachage apporte une fréquence de 490hz qui est audible lorsque l’on lance l’arduino et nous avons donc un son  d’au moins 80 dB, ce qui n’est pas du tout agréable. Pour résoudre ce souci. Nous avons changé la fréquence de hachage à une fréquence inaudible dans le programme, ce qui a considérablement diminué le bruit émis par les shakers. D’autres broches sont PWM sur l’arduino UNO mais fonctionnent par paire. En utilisant les broches 9 et 10 spécifiquement, on change dans le programme la fréquences des 2 broches, connecté entre elle par TIMER 1 : TCCR1B = TCCR1B & 0b11111000 | 0x01; (01 pour TIMER 1, il ya 3 TIMER car 6 PWM sur l’arduino UNO) 

À notre grande surprise, l’alimentation n’était pas nécessaire pour produire la fréquence que l’on souhaitait (l’amplitude de fréquence étant très basse, et le L298N ayant un” boost de puissance”, il se suffisait à lui tout seul pour fournir la puissance nécessaire). 

Du fait qu’il n’est pas optimisé pour l’amplification sonore, nous avons dû nous contenter d’une fréquence que l’on programme. Sans ça l’amplitude de nombreuses fréquences non désirées devenait importante (ce n’était pas des harmoniques, normalement). 

Le programme repose sur plusieurs principes : 

• Une durée de vibration de 7 secondes (temps durant lequel nous avons ressenti les vibrations du métro sur un point fixe) 

• Absence de vibration pendant 2 min (un métro passe toutes les 2 min en moyenne sur un même point, selon la RATP)

• Absence de vibration entre 1h30 et 5h30 du matin (les métros ne passent pas sur ces heures-ci, en moyenne, selon la RATP)  

https://www.bonjour-ratp.fr/horaires-metro/

• Nous comptions initialement simuler plusieurs pics de fréquences, mais face au matériel peu adapté, nous avons dû utiliser qu’une seule fréquence (sans ça nous obtenions des amplitudes très importantes de fréquences non souhaitées). 

On utilise aussi l’opérateur modulo pour que le temps se réinitialise toutes les heures (3 600 000ms). C’est quelque chose que l’on avait pas pris en compte en début de l’expérience mais l’arduino avait tendance à ne plus vibrer, probablement parce que le temps devenait trop important. 

Le programme arduino est le suivant : 

// --- Bibliothèques ---

#include <math.h> // Pour cos() et M_PI

const int brochePWM_A = 9; 

const int brochePWM_B = 10;

const float frequence = 60.0;   

// Ton réglage d'amplitude (volume)

const float amplitude = 100; // L’amplitude ici n’est pas celle que l’on a sur pyphox, mais c’est en la modifiant que l’on arrive à celle désirée

// --- PARAMÈTRES DU CYCLE ---

const unsigned long DUREE_ON = 7000UL;    // 7 secondes

const unsigned long DUREE_OFF = 120000UL; // 2 min

// --- CONSTANTES PRÉ-CALCULÉES ---

const float omega = 2.0 * M_PI * frequence;

const float MILLIS_EN_SECONDES = 1000.0;

const unsigned long PERIODE_LOOP = 3600000UL; // (60 * 60 * 1000)

// --- VARIABLES GLOBALES ---

unsigned long debutCycle = 0; // Chronomètre pour le cycle ON/OFF

void setup() {

 pinMode(brochePWM_A, OUTPUT);

 pinMode(brochePWM_B, OUTPUT);

 Serial.begin(115200);

 // --- LIGNE MAGIQUE (PWM Ultrasonique Timer 1) ---

 TCCR1B = TCCR1B & 0b11111000 | 0x01;

 // Initialise le début du premier cycle

 debutCycle = millis();

}

void loop() {

 unsigned long tempsActuel = millis();

 unsigned long tempsDansCycle = tempsActuel - debutCycle;

 if (tempsDansCycle < DUREE_ON) {

   // --- PÉRIODE "ON" (Vibration pendant 7s) ---

   // On utilise l'opérateur modulo (%) pour que le temps "boucle"

   float t_secondes = (float)(tempsActuel % PERIODE_LOOP) / MILLIS_EN_SECONDES;

   float cosValue = cos(omega * t_secondes);

   float V_float = 127.5 + (amplitude * cosValue);

   int V_pwm = (int)V_float;

   analogWrite(brochePWM_A, V_pwm);      

   analogWrite(brochePWM_B, 255 - V_pwm); 

 }

 else if (tempsDansCycle < (DUREE_ON + DUREE_OFF)) {

   // --- PÉRIODE "OFF" (Pause pendant 2min

   int pointMilieu = 128;

   analogWrite(brochePWM_A, pointMilieu);

   analogWrite(brochePWM_B, pointMilieu);

 }

 else {

   // --- FIN DU CYCLE (7s + 2min écoulées) ---

   // Le cycle est terminé, on le redémarre

   debutCycle = tempsActuel;

 }

}

----

Étape 3

Code R : 

Test pour les bôites de pétri 

# On importe les données excel dans Rstudio 

library(readxl)

Donnee_excel <- read_excel(file.choose())

# On renomme les colonnes pour plus de simplicité 

colnames(Donnee_excel) <- c("Boite", "Traitement", "Heures", "Nb_Graines", "Total")

library(tidyr)

Donnee_excel <- uncount(Donnee_excel, weights = Nb_Graines)

# On retire les 168 première heures, là où il n'y a pas eu de germination, et on considère que la première mesure de germination est au temps 0

Donnee_excel$Heures<-Donnee_excel$Heures-168

# On vérifie la distribution des données

hist(Donnee_excel$Heures)

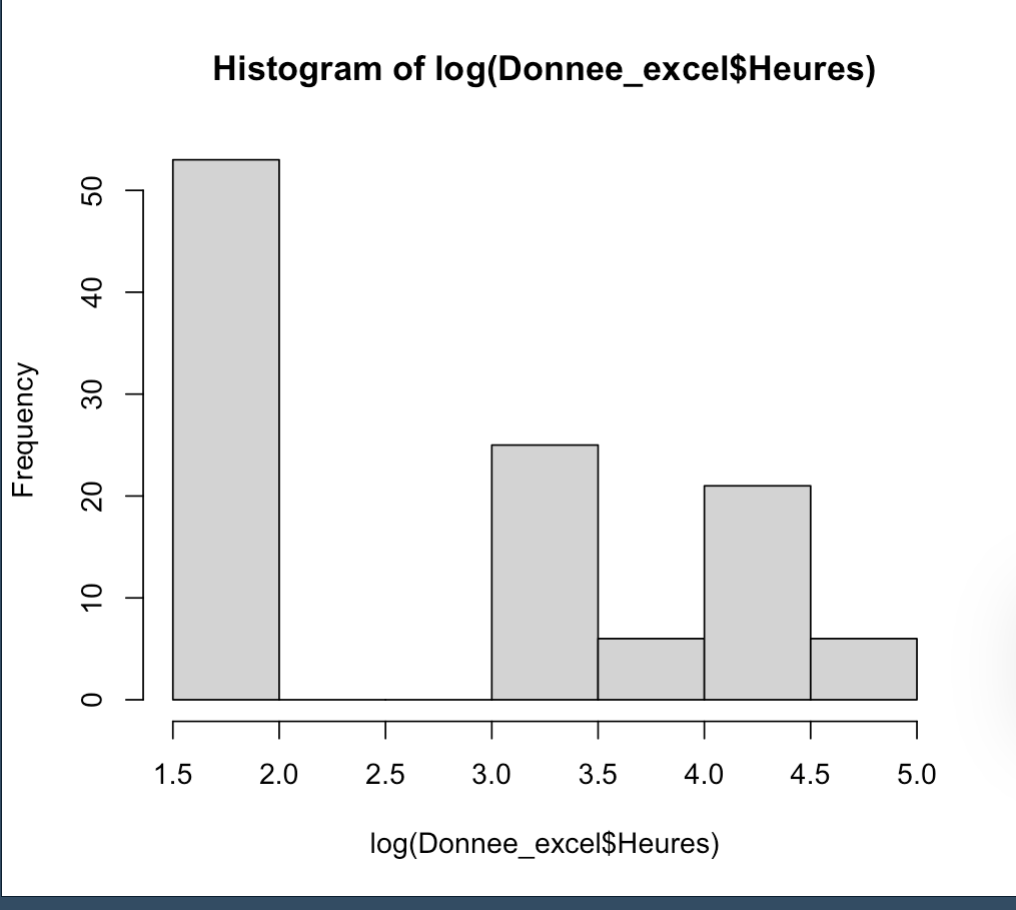
hist(log(Donnee_excel$Heures))

# La distribution ne suit pas une loi normale, on doit alors utiliser un test non paramétrique 

# On utilise alors le test de Wilcoxon afin de comparer les rangs plutôt que la moyenne 

wilcox.test(Heures ~ Traitement, data = Donnee_excel)

# On représente les données

library(ggplot2)

couleurs <- c("Contrôle" = "red", "Vibration" = "blue")

ggplot(Donnee_excel, aes(x = Traitement, y = Heures, fill = Traitement)) +

  geom_jitter(alpha = 0.3, width = 0.2, color = "black") +

  geom_boxplot(alpha = 0.7, outlier.shape = NA) +

  labs(y = "Heures après premier relevé", 

       x = "Traitement")

scale_fill_manual(values = couleurs) + 

  theme_minimal() +

  theme(legend.position = "none")

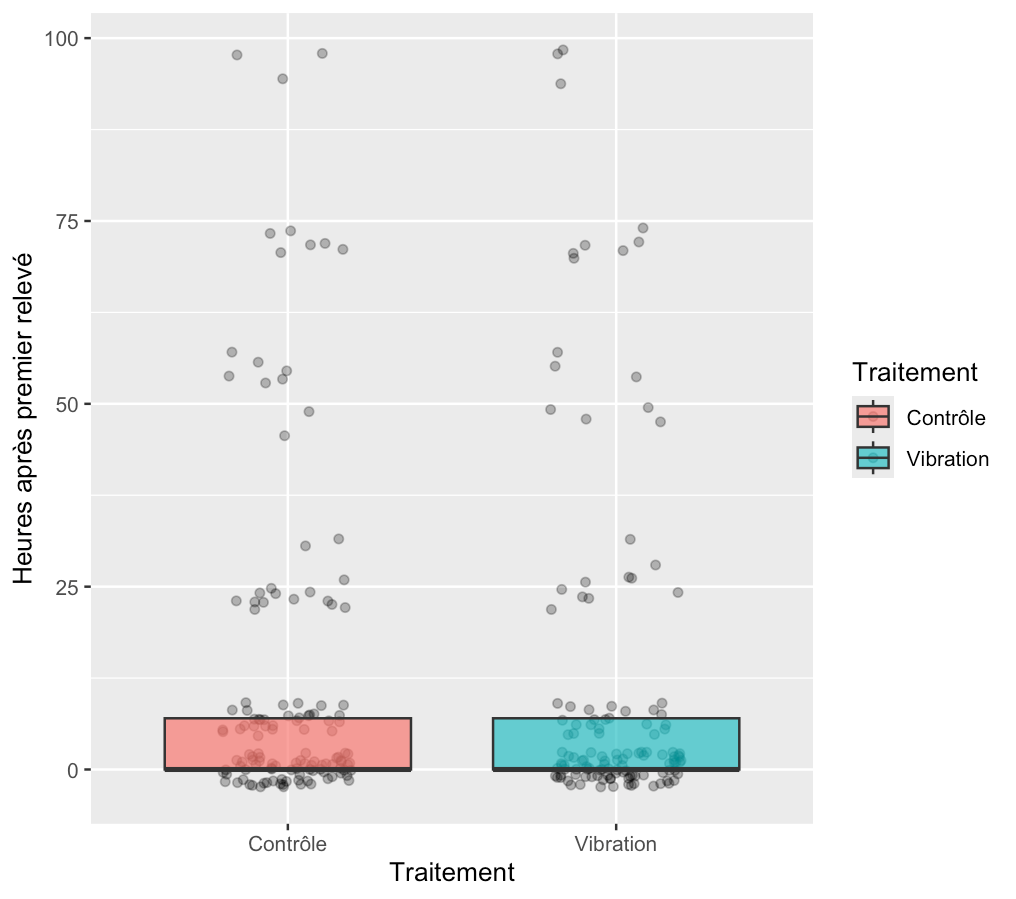
Wilcoxon rank sum test with continuity correction

data:  Heures by Traitement

W = 9185.5, p-value = 0.1384 ; alternative hypothesis: true location shift is not equal to 0 

Test pour la taille d’hypocotyle

# on importe les données excel dans Rstudio

library(readxl)

donne_excel_hypocotyle_feuille <- read_excel(file.choose(), sheet = "pousse")

donne_excel_masse <- read_excel(file.choose(), sheet = "Masse")

# On renomme les colonnes pour pouvoir les étaler et obtenir une graine par ligne 

colnames(donne_excel_hypocotyle_feuille) <- c("pot", "traitement", "longeur_hypocotyle", "Nb_feuille")

## Analyse de la longueur des hypocotyles 

# On regarde la distribution des données 

hist(donne_excel_hypocotyle_feuille$longeur_hypocotyle)

# La longueur d'un hypocotyle est un Reel Positif, on applique alors la loi GAMMA

glmG <- glm(longeur_hypocotyle ~ traitement, family = "Gamma", data = donne_excel_hypocotyle_feuille)

anova(glmG, test = "Chisq")

# On regarde le sens de significativité

tapply(donne_excel_hypocotyle_feuille$longeur_hypocotyle, donne_excel_hypocotyle_feuille$traitement, mean)

# On représente les données 

library(ggplot2)

couleurs <- c("Contrôle" = "red", "Vibration" = "blue")

ggplot(donne_excel_hypocotyle_feuille, aes(x = traitement, y = longeur_hypocotyle, fill = traitement)) +

  geom_jitter(width = 0.2, size = 2, alpha = 0.4, color = "black") +

  # alpha = 0.7 pour voir un peu les points derrière

  # outlier.shape = NA car on affiche déjà tous les points

  geom_boxplot(alpha = 0.7, outlier.shape = NA) +

   labs(

       y = "Longueur de la hypocotyle (cm)",

       x = "Traitement") +

  scale_fill_manual(values = couleurs) +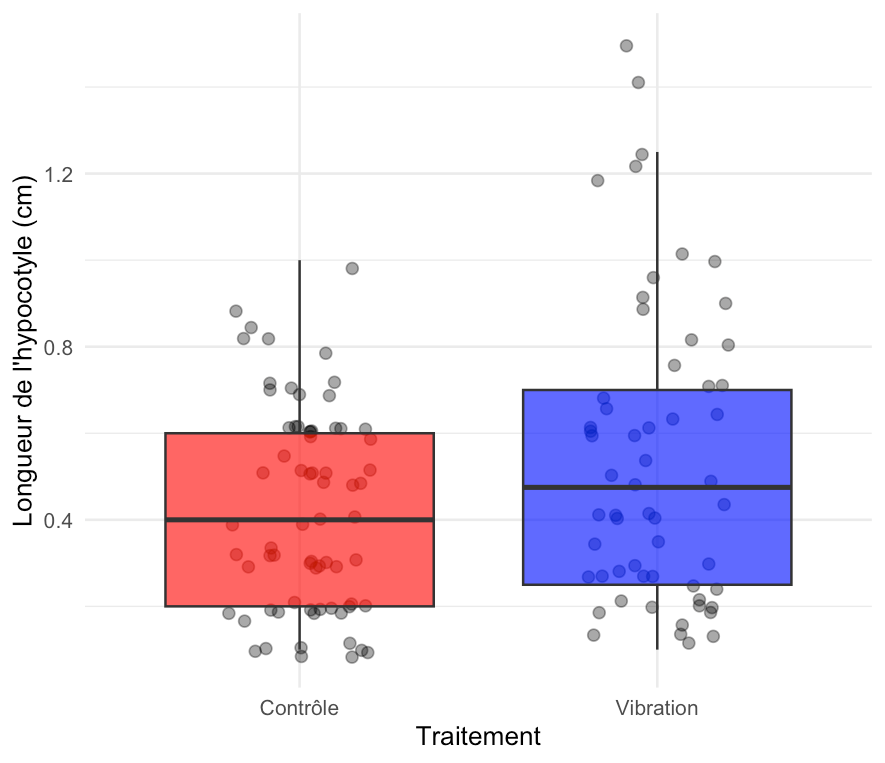

  theme_minimal()

   Df Deviance Resid. Df Resid. Dev Pr(>Chi)  

NULL                         127     51.952           

traitement  1   1.8966       126     50.056  0.02002 *

---

Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Mean “Contrôle” : 0.4228571 ; Mean “Vibration” : 0.5396552 

# Dans cette démarche, nous avons considéré les cotylédons comme des feuilles. Comme certaines feuilles ont uniquement

# des cotylédons (Nb_feuille = 2), il serait intéréssant de regarder le nombre de plantes ayant eu de vraies feuilles. 

# On crée une colonne binaire : Si Nb_feuille est strictement supérieur à 2, on met 1 (Succès).

# Sinon (donc si c'est égal à 2), on met 0 (Échec) → cotyledon

donne_excel_tige_feuille$cotyledon <- ifelse(donne_excel_tige_feuille$Nb_feuille > 2, 1, 0)

glmB <- glm(cbind(Nb_feuille, cotyledon)~ traitement,

            family = binomial(link = "logit"), data = donne_excel_tige_feuille)

anova(glmB, test = "Chisq")

 Df Deviance Resid. Df Resid. Dev Pr(>Chi)

NULL                         127     42.198         

traitement  1  0.44514       126     41.753   0.5046

Test pour le nombre de feuille 

## Analyse du nombre de feuille 

# On regarde la distribution des données 

hist(donne_excel_hypocotyle_feuille$Nb_feuille)

# La distribution ne suit pas une loi normale, on doit alors utiliser un test non paramétrique 

# On utilise alors le test de Wilcoxon afin de comparer les rangs plutôt que la moyenne 

wilcox.test(Nb_feuille ~ traitement, data = donne_excel_hypocotyle_feuille)

# On représente les données

library(ggplot2)

couleurs <- c("Contrôle" = "red", "Vibration" = "blue")

ggplot(donne_excel_hypocotyle_feuille, aes(x = traitement, y = Nb_feuille, fill = traitement)) +

  geom_jitter(alpha = 0.3, width = 0.2, color = "black") +

  geom_boxplot(alpha = 0.7, outlier.shape = NA) +

  labs(y = "Nombre de feuille par plante", 

       x = "Traitement")

scale_fill_manual(values = couleurs) + 

  theme_minimal() +

  theme(legend.position = "none")

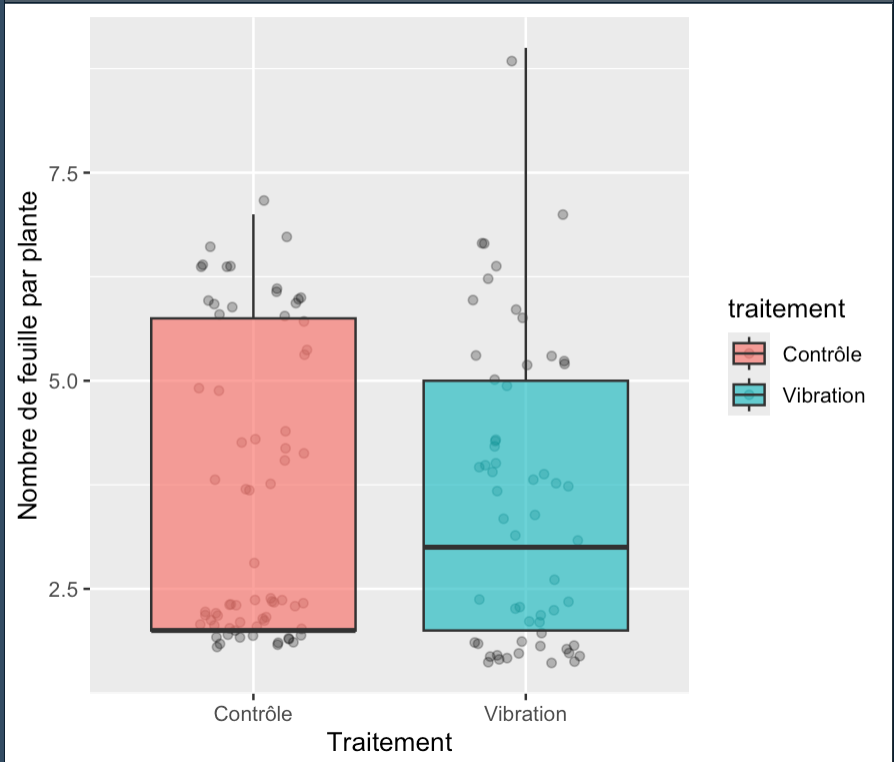
Wilcoxon rank sum test with continuity correction

data:  Nb_feuille by traitement

W = 1971, p-value = 0.7649

alternative hypothesis: true location shift is not equal to 0

Test pour la masse fraîche par plante 

## Analyse de la masse fraiche aérienne par pot 

# On regarde la distribution des données 

hist(donne_excel_masse $`masse/Nb`)

# La distribution ne suit pas une loi normale, on doit alors utiliser un test non paramétrique 

# On utilise alors le test de Wilcoxon afin de comparer les rangs plutôt que la moyenne 

wilcox.test(`masse/Nb` ~ traitement, data = donne_excel_masse)

# On change l'unité de le masse en mg

donne_excel_masse$masse_mg <- donne_excel_masse$`masse/Nb` * 1000

# On représente les données 

library(ggplot2)

couleurs <- c("Contrôle" = "red", "Vibration" = "blue")

ggplot(donne_excel_masse, aes(x = traitement, y = masse_mg, fill = traitement)) +

  geom_jitter(alpha = 0.3, width = 0.2, color = "black") +

  geom_boxplot(alpha = 0.7, outlier.shape = NA) +

  labs(y = "Masse par plante (mg)", 

       x = "Traitement")

scale_fill_manual(values = couleurs) + 

  theme_minimal() +

  theme(legend.position = "none")

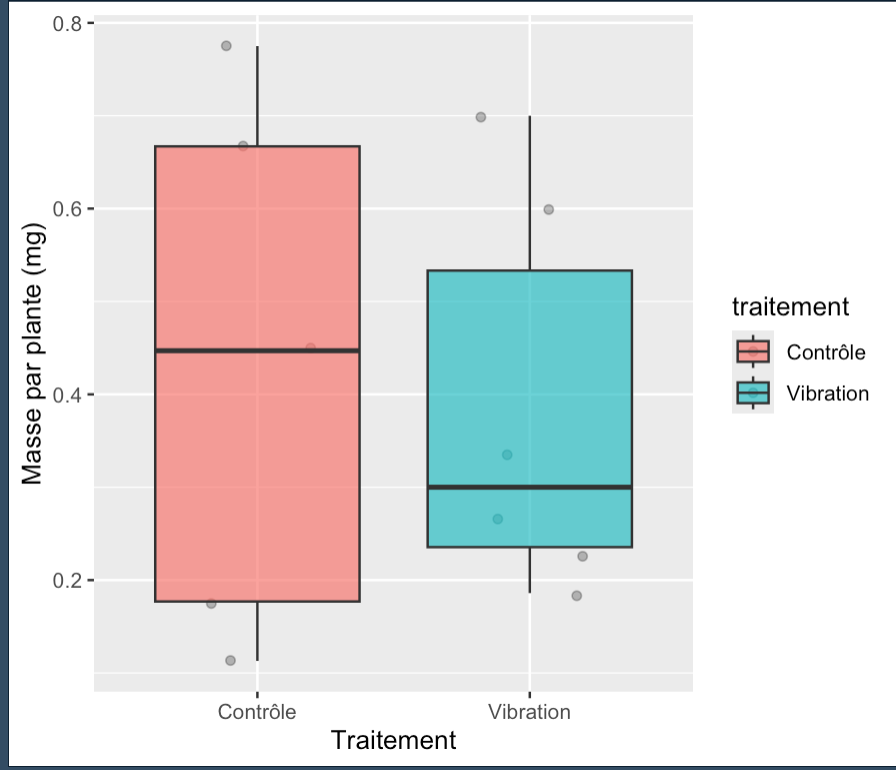
Wilcoxon rank sum exact test

data:  masse/Nb by traitement

W = 15, p-value = 1

alternative hypothesis: true location shift is not equal to 0