Plis en mousse ⛰️
Informations
- Contacts : Elphège et Ludivine (ludivine.fars@etu.sorbonne-universite.fr)
- Etudes : Licence 3 - Majeure Biologie, Mineure Sciences de la Terre
- Dates du projet : 24 Janvier 2025 au 24 Mai 2025
- Responsables de l'UE LU3ST062 : Loïc Labrousse et Pierre Théry
- Responsable Projet Plis en Mousse : Claudio Rosenberg
Pli en Mousse
Présentation
Ce projet est né suite à la demande de Claudio Rosenberg de faire un modèle pédagogique de pli ayant les caractéristiques suivantes : une couche de viscosité (µ1) différente de sa matrice (µ2), matrice pouvant être modélisée par deux couches d'un même constituant.
En géologie, les matériaux terrestres peuvent être déformés de manière continue de 2 façons : par des déformations homogènes et/ou hétérogènes. Une déformation homogène, c'est quand deux surfaces parallèles dans l'état initial restent parallèles dans l'état final, on peut le modéliser par une translation. Ces déformations sont soit associées à un aplatissement/étirement (cisaillement pur, coaxial), soit s'accompagnent d'une composante rotationnelle (cisaillement simple, non coaxial).
Cependant, les matériaux terrestres ne s'harmonisent que rarement à une déformation dite homogène. En effet, de part le fait qu'ils soient de composition donc de viscosité et résistance différentes, ils auront tendance plutôt à induire des déformations hétérogènes. Les structures produites les plus classiques formées par ces déformations hétérogènes sont les plis. Ces derniers se forment lorsqu'une surface, initialement plane, modifie sa forme sous l'effet de contraintes tectoniques sans casser. Les plis sont des déformations périodiques qui résultent d'instabilités de cisaillement dues à des contrastes de résistance et qui se développent selon une certaine longueur d'onde.
Plus il y a un contraste de viscosité entre la matrice et la couche au sein de cette matrice, plus la longueur d'onde du pli formé sera importante lorsqu'il y a contrainte mise sur la structure. Cela est notamment modélisé par une relation, établie par Biot (en 1961) :
Pour étudier des plis, on doit regarder la longueur d'onde des plis (distance entre les lignes d‘inflexion d‘un couple antiforme-synforme), leur amplitude (demi-distance entre les tangentes des charnières des antiformes ou synformes), mais aussi la disposition des plans axiaux des plis.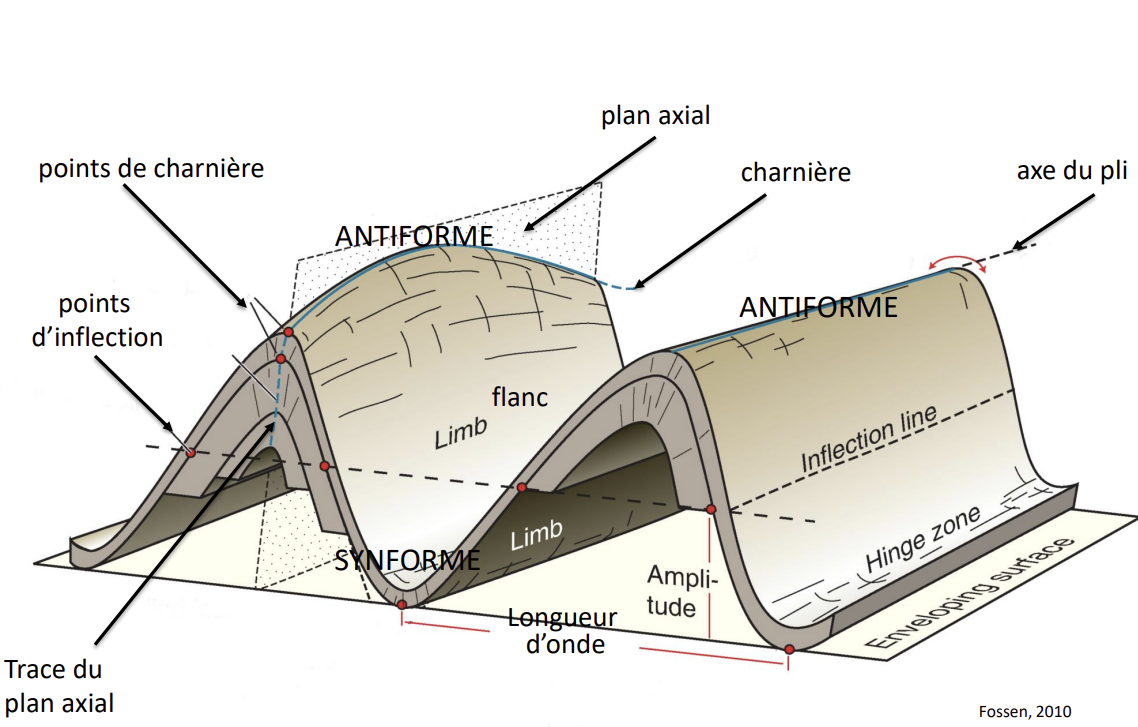
Dans notre cas, nous allons essayer de produire un modèle avec une couche d'une certaine viscosité (µ1) se retrouvant plissée entre deux couches (considérées ici comme un encaissant ou une matrice) d'une viscosité différente (µ2) sous d'un raccourcissement parallèle.
Nous avons choisi, pour avoir 2 viscosités différentes, de la mousse comme matrice et du silicone comme couche à plisser. Notre idée d'utiliser de la mousse et du silicone, vient quant à elle du visionnage d'une vidéo (sur Youtube) de modélisation d'un pli grâce à de la mousse et du silicone, modélisation produite par Markus Beckers, Michael Ketterman, Dennis Laux et Janos Urai : https://youtu.be/jd3hG2PNdUo?si=tqjAjx20PR8gEWnk
![]()
Nous rajouterons un cadrillage, dessiné sur chacun de nos modèles, permettant d'avoir des points d'intersections disposés sur la mousse et à la limite mousse/silicone afin de suivre les déplacements de ces points et ainsi mieux comprendre et visualiser les déformations du silicone, mais aussi de la mousse lorsque les contraintes sont effectives. Nous allons, par la suite, utilisé un code informatique Python, créé par Loïc Labrousse, que nous allons modifié afin qu'il soit plus simple d'utilisation, afin de créer des ellipses de vitesses de déformations déduites des points d'intersections précédemment dessinés, permettant d'avoir des données calculées plus précises que de simples observations visuelles.
Matériel
Pour le 1er modèle
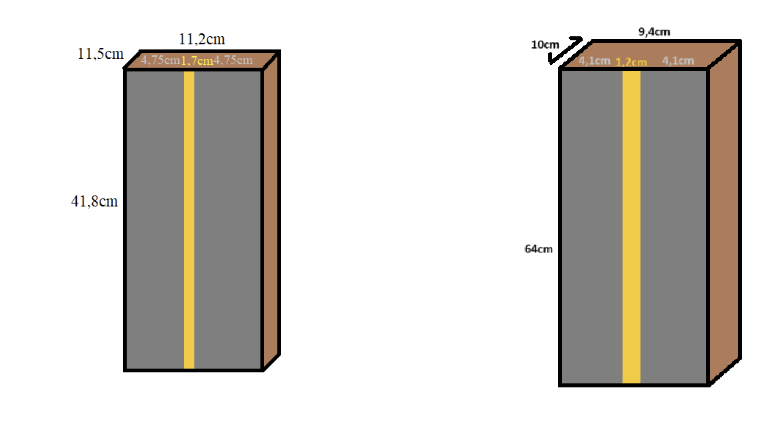
- 2 plaques de mousse synthétique d'isolation à cellules ouvertes avec un diamètre cellulaire ~ 1mm (1000 µ) de dimension : 41.8 cm x 4.75 cm x 11.5 cm
- Du silicone RTV 151 (Esprit Composite) dans l'espace de la couche de dimensions 41.8 cm x 1.7 cm x 11.5 cm (donc de volume d'environ 820cm3) + dans le fond de dimension 41,8 cm x 11,2 cm x 0,5cm (donc de volume d'environ 235cm3), de densité d=1,25 et d'une viscosité de 8000 mPa.s et d'une dureté de (Shore A) 20. Sa durée de durcissement est de 12h
- Le catalyseur/durcisseur correspondant (vendu avec)
- Talc
- Plaques en cartons
- Scotch
- Cutter et paire de ciseaux
- Colle forte
- Feutres marqueurs de couleurs (notamment pour le cadrillage)
- Une balance
- Un contenant pour mélanger le silicone et le catalyseur
- Quelque chose pour mélanger le silicone et le catalyseur (cuillère, agitateur)
Pour le 2nd modèle
- 2 plaques de mousse synthétique d'isolation à cellules ouvertes avec un diamètre cellulaire ~ 1mm (1000 µ) de dimension : 64 cm x 4,1 cm x 10 cm
- 1 couche de silicone RTV 151 au centre de dimension : 64 cm x 1.2 cm x 10 cm , de densité d=1,051 à 20°C, d'une viscosité 27,95 mPa.s, et d'une dureté de (Shore A) 13
- Le catalyseur/durcisseur correspondant (vendu avec)
- Talc
- Plaques en cartons
- Scotch
- Cutter et paire de ciseaux
- Colle forte
- Feutres marqueurs de couleurs (notamment pour le cadrillage)
- Une balance
- Un contenant pour mélanger le silicone et le catalyseur
- Quelque chose pour mélanger le silicone et le catalyseur (cuillère, agitateur)
Protocole de Fabrication des Modèles
Dimensions de notre premier modèle (à gauche) puis pour notre second modèle (à droite) :
Protocole :
0 - Créer un carton avec les dimensions voulues où nous y calleront les 2 mousses et où nous feront couler le silicone. Dans notre cas, nous avons juste, à partir de plaques de cartons coupées avec les dimensions voulues (voir par exemple image ci-dessus) et de scotch, formé un moule. L'utilité du carton comme moule est qu'il suffit de couper le scotch avec un cutter à la dernière étape pour démouler certaines faces.
1 - Mettre du talc au fond du carton/du moule
1' - Couler du silicone mélangé à son catalyseur sur le fond (pour éviter que le silicone central coule totalement vers le bas)
Protocole Masse Silicone et Catalyseur
Pour avoir la bonne masse de silicone et de catalyseur, il faut prendre en compte plusieurs données. Le rapport silicone/catalyseur en premier lieu, ici de 100:5 (c'est-à-dire que pour 100g au total, il faut 5g de catalyseur et 95g de silicone), la densité du silicone et du catalyseur, ainsi que le volume dans lequel il sera versé (selon les dimensions de notre moule, c'est-à-dire selon le volume de silicone que l'on souhaite au fond permettant l'accrochage des mousses (étape 1') ou les dimensions de la place qu'aura la couche de silicone centrale (étape 3)). Autrement dit, on a m = ρ*V avec m en g, ρ en g/cm3 et V en cm3 . En rajoutant les proportions, cela donne m=0,95(ρsilicone*Vsilicone) + 0,05(ρcatalyseur*Vcatalyseur).
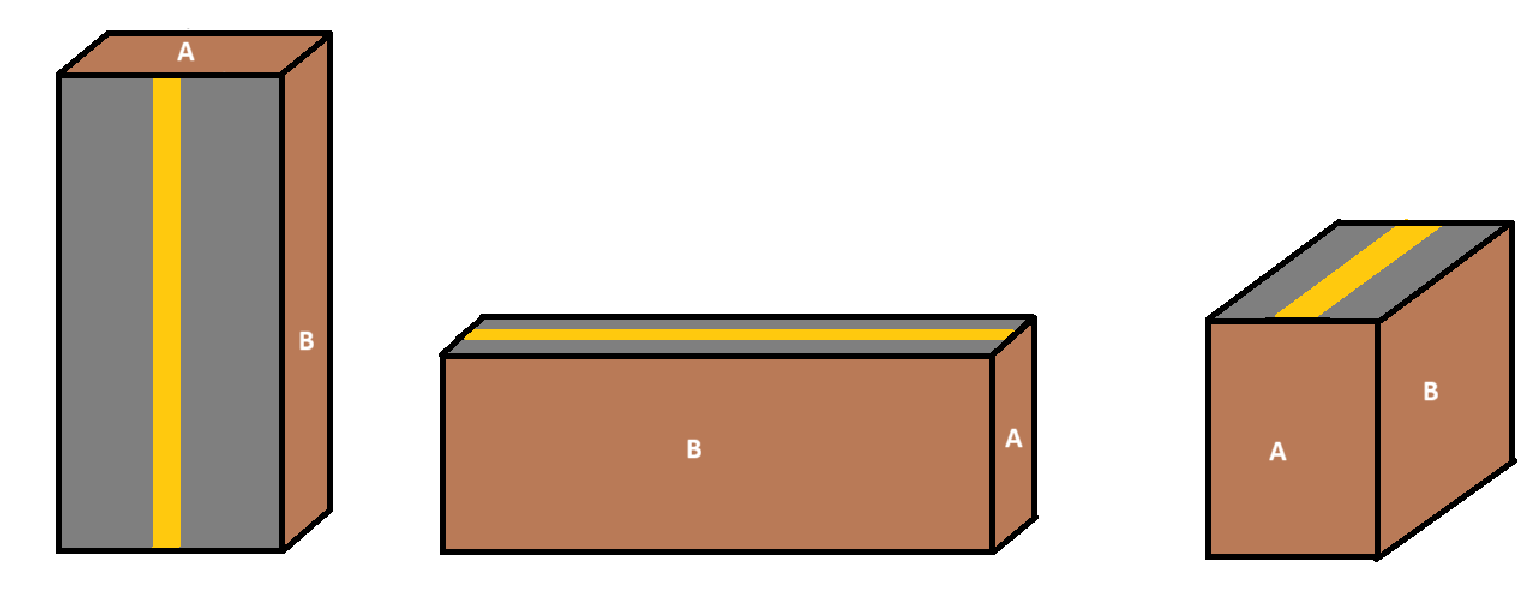
2 - Enduire généreusement de talc les mousses les faces qui seront en contact avec le silicone : les faces du bas en contact avec la base et celles, plus grandes, qui seront en contact avec la couche centrale du silicone (c'est-à-dire sur les schémas ci-dessus les faces entre le gris de la mousse et le jaune du silicone)
2' - Avant de poser les 2 mousses sur le fond, ajouter de la colle forte sur les faces de mousse qui seront en contact avec les côtés extérieurs du modèles (face A sur schémas ci-dessus) où seront appliquées les contraintes (pour meilleures préhension du modèle)
2'' - Poser des 2 mousses sur le fond (avant que le silicone se soit trop rigidifié de telle sorte que le silicone colle bien aux mousses) en vérifiant bien que la colle agit des deux côtés extérieurs également
3 - Couler le silicone entre les 2 mousses peu à peu
4- Après avoir attendu (au moins 24h) que le silicone se soit rigidifié, enlever le moule, c'est-à-dire décoller les deux faces les plus grande du moule/ du carton (faces B sur les schémas ci-dessus) ainsi que la base. Si suffisamment de talc a été mis au fond, normalement enlever la base n'est pas compliqué, et les deux faces les plus grandes étant celles sans contact avec silicone ou colle, il est normalement simple de les enlever aussi.
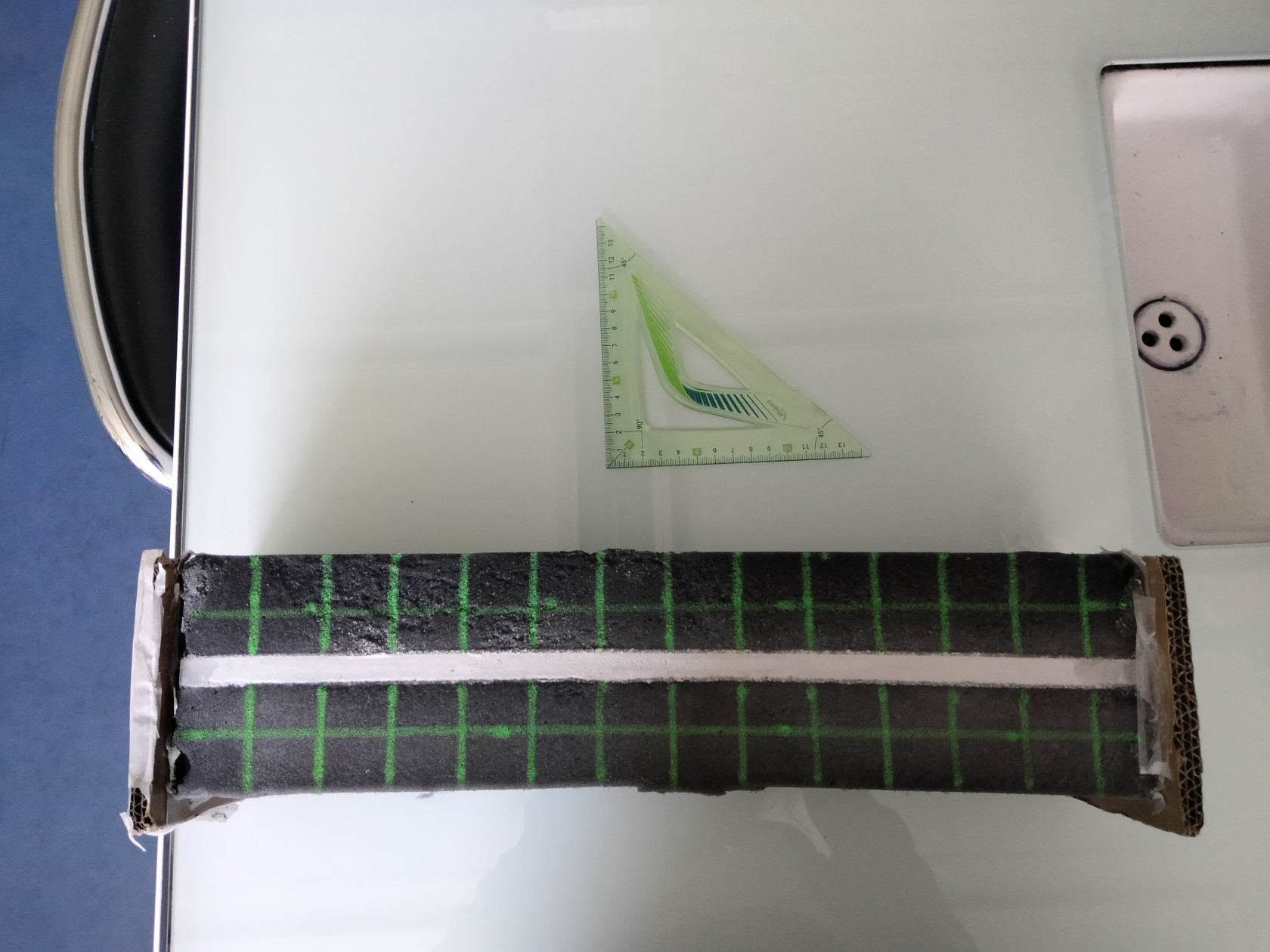
5 - Dessiner le cadrillage avec un feutre marqueur de couleur différente de la mousse
 Schéma du montage étape par étape puis schéma du cadrillage
Schéma du montage étape par étape puis schéma du cadrillage
Code Informatique
Code Python
import numpy as np
from matplotlib import pyplot as plt
from matplotlib import image as img
from scipy.spatial import Delaunay # pour tracer les triangles
from matplotlib import colormaps as cmp
from matplotlib import colors as cl
from matplotlib import cm
import matplotlib
matplotlib.use('Qt5Agg')
def pick_points(image, n):
# Permet de piquer les points d'un repère et de les mettre à l'échelle
fig, ax = plt.subplots()
plt.imshow(image)
# Pointer le repère dans cet ordre : origine, axe des x, axe des y
plt.title('Cliquer sur les 3 points du repère O, X, Y')
R = plt.ginput(3, show_clicks=1)
print("Points sélectionnés pour le repère (O, X, Y) :")
print(R) # Affiche la structure exacte des points
R = np.array(R)
print("Structure de R après conversion en numpy array :")
print(R)
# Vérification des dimensions
if R.ndim != 2 or R.shape[1] != 2:
print(f"Erreur dans la structure de R : R.ndim={R.ndim}, R.shape={R.shape}")
raise ValueError("Les points sélectionnés ne sont pas sous forme de coordonnées 2D")
ax.plot(R[:, 0], R[:, 1], 'r+')
# Pointer les noeuds de la grille (clics illimités jusqu'à touche)
plt.title("Cliquez les noeuds de la grille, puis appuyez sur Entrée pour terminer")
print("🖱 Cliquez les noeuds... puis appuyez sur Entrée quand vous avez terminé.")
points = []
compteur = 1
while True:
pts = plt.ginput(1, timeout=0)
if not pts:
break
points.append(pts[0])
print(f"🖱 Point {compteur} cliqué : {pts[0]}")
ax.plot(pts[0][0], pts[0][1], 'g+')
plt.draw()
compteur += 1
plt.show()
N = np.array(points)
print("✅ Total de points cliqués :", len(N))
# Vérification des dimensions
if N.ndim != 2 or N.shape[1] != 2:
print(f"Erreur dans la structure de N : N.ndim={N.ndim}, N.shape={N.shape}")
raise ValueError("Les noeuds sélectionnés ne sont pas sous forme de coordonnées 2D")
ax.plot(N[:, 0], N[:, 1], 'r+')
plt.show()
# Fermer la fenêtre après l'affichage
plt.close(fig) # Ajout de plt.close pour fermer la fenêtre après que l'utilisateur ait sélectionné les points.
# Mettre les distances à l'échelle
unite_x = R[1, 0] - R[0, 0]
unite_y = R[2, 1] - R[0, 1]
N[:, 0] = N[:, 0] / unite_x
N[:, 1] = N[:, 1] / unite_y
return N
def vdef_de_deplt(xi, yi, xf, yf):
# calcule les vitesses de deplacements a partir des positions et vitesses des stations
xi = xi - np.mean(xi)
yi = yi - np.mean(yi)
xf = xf - np.mean(xf)
yf = yf - np.mean(yf)
A = np.array([[np.sum(xi*xi), np.sum(xi*yi)],
[np.sum(xi*yi), np.sum(yi*yi)]])
B1 = np.array([np.sum(xi*xf), np.sum(yi*xf)])
B1 = B1.transpose()
B2 = np.array([np.sum(xi*yf), np.sum(yi*yf)])
B2 = B2.transpose()
X1 = np.linalg.lstsq(A,B1,rcond = None)
X2 = np.linalg.lstsq(A,B2,rcond = None)
ab = X1[0]
cd = X2[0]
D = ab[0]*cd[1] - ab[1]*cd[0]
C = ab[0]**2 +ab[1]**2 + cd[0]**2 + cd[1]**2
X = np.sqrt(0.5*(C + np.sqrt(C**2 - 4*D**2))) # étirement
Z = np.sqrt(0.5*(C - np.sqrt(C**2 - 4*D**2))) # raccourcissement
Theta = 0.5*np.arctan2(2*(ab[0]*cd[0] + ab[1]*cd[1]),(ab[0]**2 +ab[1]**2 - cd[0]**2 - cd[1]**2))
dil = D - 1
return X, Z, Theta, dil
def plot_fleche(x, y, val, angle, coul): # dessine les axes de l'ellipsoide de deformation
echelle = 0.1 # pour mettre à l'echelle
taille_fleche = 0.01 # taille de la fleche
dx = val*echelle*np.cos(angle)
dy = val*echelle*np.sin(angle)
plt.arrow(x, y, dx, dy, color = coul, length_includes_head = True, width = taille_fleche)
plt.arrow(x, y, -dx, -dy, color = coul, length_includes_head = True, width = taille_fleche)
n_n = 90 # nombre de noeuds à pointer
init = img.imread('SansContraintes.jpg') # nom des fichiers ... ils doivent etre ds le meme rep que le .py
fin = img.imread('AvecContraintes.jpg')
N_init = pick_points(init,n_n)
N_fin = pick_points(fin,n_n)
# generer les triangles de Delaunay
triangles_i = Delaunay(N_init)
# inverser la matrice de déplacement
X, Z, Theta, dil = [], [], [], []
for tri in triangles_i.simplices:
xi, yi = N_init[tri,0], N_init[tri,1]
xf, yf = N_fin[tri,0], N_fin[tri,1]
r1, r2, r3, r4 = vdef_de_deplt(xi, yi, xf, yf)
X.append(r1)
Z.append(r2)
Theta.append(r3)
dil.append(r4)
X = np.array(X)
Z = np.array(Z)
Theta = np.array(Theta)
dil = np.array(dil)
norm_def = np.hypot(X,Z) # hypothenuse
# trouver les barycentres des triangles
coordc = []
for tri in triangles_i.simplices:
xc = np.mean(N_fin[tri,0])
yc = np.mean(N_fin[tri,1])
coordc.append([xc, yc])
coordc = np.array(coordc)
cmap = cmp['RdBu']
cmap = cmap.reversed()
lim_coul = [1, 2] # a modifier
fig1, ax1 = plt.subplots()
ax1.axis('equal')
plt.plot(N_fin[:,0], N_fin[:,1], 'ko')
plt.tripcolor(N_fin[:,0], N_fin[:,1], triangles_i.simplices, norm_def,
color = 'black', linewidth = 0.5, cmap=cmap, vmin=lim_coul[0], vmax = lim_coul[1])
norm = cl.Normalize(lim_coul[0], lim_coul[1])
fig1.colorbar(cm.ScalarMappable(norm=norm, cmap=cmap), ax=ax1,
orientation = 'horizontal', location = 'bottom', label = 'deformation finie')
for x, y, v, Th in zip(coordc[:,0], coordc[:,1], X, Theta):
plot_fleche(x, y, v, Th, 'white')
for x, y, v, Th in zip(coordc[:,0], coordc[:,1], Z, Theta+np.pi/2):
plot_fleche(x, y, v, Th, 'black')
plt.show()
Les fichiers "SansContraintes.jpg" et "AvecContraintes.jpg" sont les images du modèle quadrillé sans contraintes puis avec (le deuxième étant le prototype à l'état plissé) suivantes
Pour faire fonctionner le code avec un autre modèle, donc d'autres photos, il suffit soit de renommer les photos avec ces noms, soit de modifier le code. Par exemple, nous, nous avons reproduit l'expérience avec notre 2nd prototype :
Résultats
Pour le premier modèle :
Le talc a bien fonctionné, il n'y a pas de gradient de silicone dans la mousse. Cela permet de vraiment bien coller la couche de silicone et les mousses sans décollement. Cela fonctionne relativement bien, mais nous ne pouvons pas faire plus de 2 plis (et pour 2 plis, seul Claudio a réussi, nous on n'est pas assez fortes pour faire plus d'un seul pli). Claudio propose d'essayer, pour un 2ème prototype, un silicone moins visqueux.
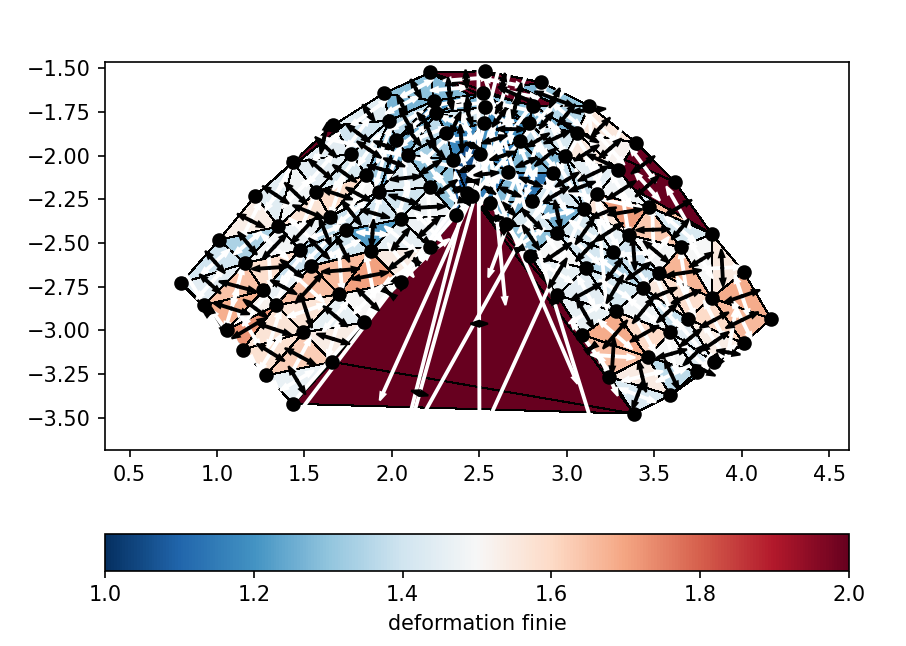
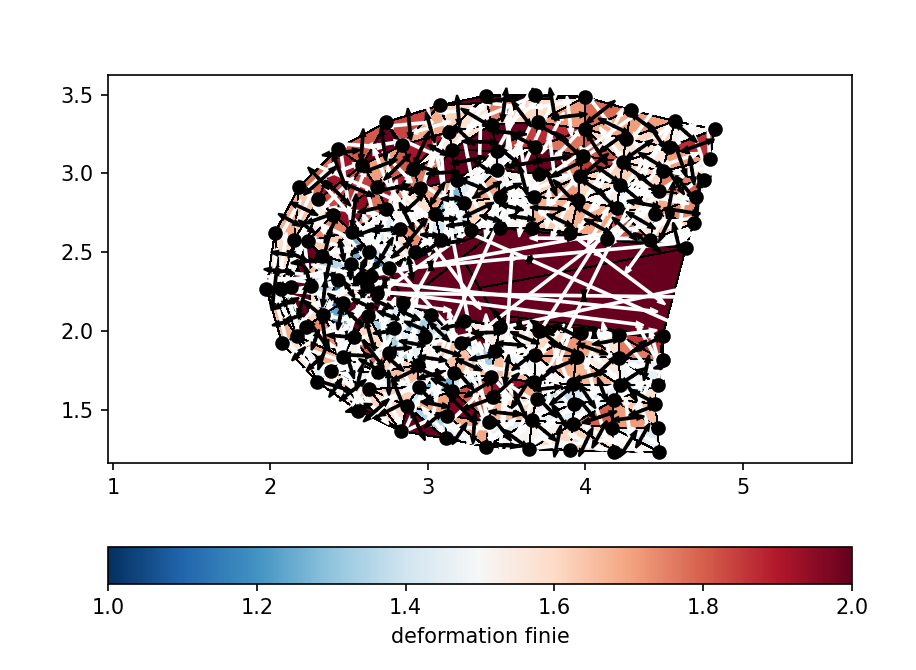
Avec le quadrillage, on voit qu'il y a plus de déformation au niveau de l'axe du pli que sur les côtés. Maintenant, observons ce que donne le code python :
On a ici une représentation par triangulation (de Delaunay) de la translation et de la déformation entre le prototype non plissé et le prototype plissé. Les flèches noires et blanches indiquent les sens de raccourcissement et d'allongement respectivement. Le gradient de couleur représente quand à lui la vitesse de déformation, donc indique les endroits qui ont été plus affecté par les contraintes. On observe que la déformation est plus importante sur la mousse que sur le silicone (couche centrale), notamment au niveau de la charnière du pli.
Pour le deuxième modèle :
Nous arrivons à faire plusieurs plis mais le talc a mal fonctionné, il y a un gradient de silicone dans la mousse... De plus, nous avons dû utiliser plus de silicone que prévu (peut-être est-ce dû à ce gradient ? d'erreurs de calculs de notre part, ou de biais physico-chimiques que nous ne maitrisons pas ? de mauvaises données sur le site du vendeur ?) La silicone au fond à par conséquent trop collé à la mousse, nous n'avons pas réussi à bien décoller sans arracher la mousse. Ainsi, problématique de talc ou problématique de silicone ? Conclusion : prototype à améliorer. De plus, le silicone semble plus dur que le premier, il est plus complexe que plisser l'objet car le silicone n'est pas assez souple, mais encore une fois, cela peut être dû au gradient.
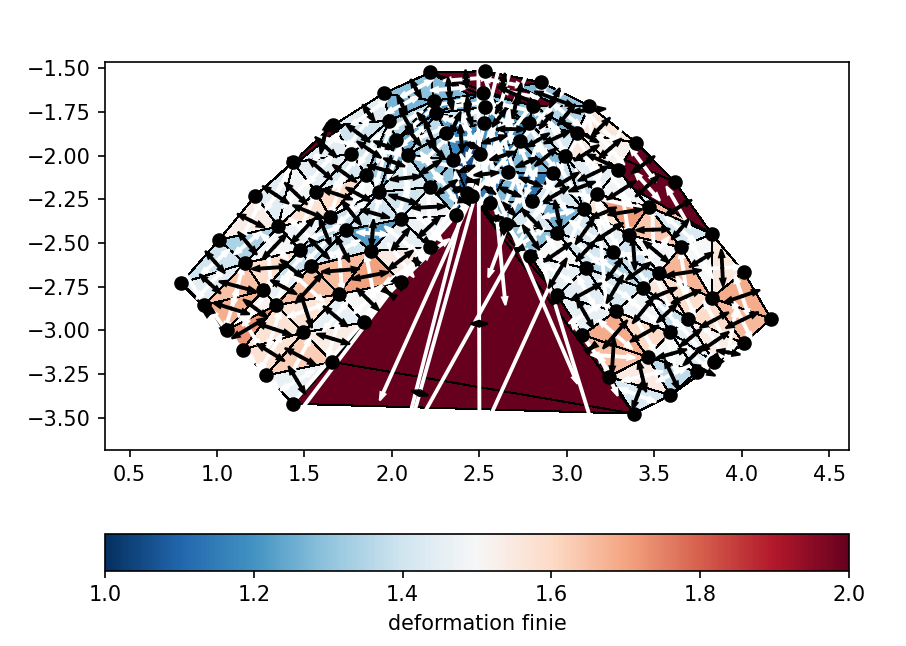
Concernant le résultat avec le code informatique, nous observons ceci :
On observe ici pour ce modèle qu'il y a plus de déformation, notamment dû au fait que nous avions mis plus de contraintes. Mais cela permet aussi de voir qu'il semble y avoir, encore une fois, moins de déformation au niveau du silicone que de la mousse. Ainsi, le silicone étant plus visqueux que la mousse, il résiste mieux à la contrainte et se déforme moins, ayant pour effet de mettre plus de contraintes (pour équilibrer) sur sa matrice, ici la mousse, qui se déforme ainsi plus distinctement. D'ailleurs, dans les deux modèles, on peut même observer qu'il semblerait y avoir plus de déformations sur la mousse proche du silicone, confirmant cette théorie.
Ce qui peut être amélioré
- Il serait intéressant de trouver quelque chose pour stabiliser la structure si utilise la structure de haut en bas en longueur et ainsi permettre de plus facilement faire 2 plis de suite, sinon c'est compliqué de créer une contrainte suffisante avec seulement notre propre force personnelle
- La colle ne fonctionne pas sur la mousse, ou pas longtemps, trouver une autre solution
- Trouver quelque chose pour éviter le gradient produit par certains silicones (le talc n'ayant pas suffit pour le modèle 2) -> peut-être reprendre les silicones de Esprit Composite répondant mieux au talc .
- Peut-être créer un modèle moins haut ? faire une couche de silicone moins épaisse (c'est compliqué cependant, au moment du coulage du silicone)
Bibliographie
- Claudio Rosenberg (2024) - Cours de Tectonique de Licence 2 de Géosciences à Sorbonne Université
- Loïc Labrousse, Philippe Yamato (2024) - La déformation des roches, De l'analyse structurale à la définition mécanique de la lithosphère - Collection Sciences Sup, Edition Dunod
- Janos Urai, Markus Beckers, Michael Ketterman, Dennis Laux (2010) - Folding of a single, thick silicone layer (Structural Geology, analogue modelling) : https://youtu.be/jd3hG2PNdUo?si=tqjAjx20PR8gEWnk
- Abe, Steffen, et Janos L. Urai. « Discrete Element Modeling of Boudinage: Insights on Rock Rheology, Matrix Flow, and Evolution of Geometry ». Journal of Geophysical Research: Solid Earth, vol. 117, no B1, janvier 2012, p. 2011JB008555. DOI.org (Crossref), https://doi.org/10.1029/2011JB008555.
- Bons, Paul D., et Janos L. Urai. « An Apparatus to Experimentally Model the Dynamics of Ductile Shear Zones ». Tectonophysics, vol. 256, no 1‑4, mai 1996, p. 145‑64. DOI.org (Crossref), https://doi.org/10.1016/0040-1951(95)00161-1
- Livio, Franz, et al. « Growth of Bending-Moment Faults Due to Progressive Folding: Insights from Sandbox Models and Paleoseismological Implications ». Geomorphology, vol. 326, février 2019, p. 152‑66. DOI.org (Crossref), https://doi.org/10.1016/j.geomorph.2018.02.012.
- Poulet, M. « Apport des expériences de mécaniques des roches à la géologie structurale des bassins sédimentaires ». Revue de l’Institut Français du Pétrole, vol. 31, no 5, septembre 1976, p. 781‑822. DOI.org (Crossref), https://doi.org/10.2516/ogst:1976026.
Journal de Bord
24 Janvier 2025
Explication du Projet : Modélisation de plis à partir de 3 couches de 2 viscosités différentes (afin de déterminer des longueurs d'onde en fonction des différences de viscosité) telle que :
Idées Hypothèse 1 :
- Coudre 2 types de mousses entre elles
- Utiliser 1 couche de silicone entre 2 couches de mousses différentes
- Utiliser 4 couches de silicone avec 2 viscosités différentes
- Utiliser une résine qui rentrerait dans la mousse poreuse - mais attention à ne pas créer de gradient
Références données par Claudio :
- Janos Urai -> Aachen = Aix-La-Chapelle -> Rwth
Vidéos trouvées :
“Pliage d'une couche de silicone unique et épaisse, intégrée dans une matrice de mousse isolante. Cette playlist présente quelques films sur le pliage analogique de couches de silicone intégrées dans une matrice de mousse. Nous avons construit ces modèles pour démontrer le pliage d'une et de plusieurs couches dans des roches en classe, en suivant plus ou moins les figures du livre de John Ramsay. Ils sont suffisamment grands pour être utilisés en classe, assez légers et peuvent être déformés à la main devant la classe. Ils peuvent être réutilisés. Nous avons utilisé des élastomères compressibles plutôt que des matériaux visqueux pour obtenir le bon effet, car cela permet de modifier le volume et même de former une sorte de clivage dans le plan axial. Si l'intérêt est suffisant, nous pourrions envisager d'offrir ces modèles sous la forme d'un kit d'enseignement et de demander à une entreprise de produire un lot”
Articles de Janos Urai pouvant être intéressants :
- Abe, Steffen, et Janos L. Urai. « Discrete Element Modeling of Boudinage: Insights on Rock Rheology, Matrix Flow, and Evolution of Geometry ». Journal of Geophysical Research: Solid Earth, vol. 117, no B1, janvier 2012, p. 2011JB008555. DOI.org (Crossref), https://doi.org/10.1029/2011JB008555.
- Bons, Paul D., et Janos L. Urai. « An Apparatus to Experimentally Model the Dynamics of Ductile Shear Zones ». Tectonophysics, vol. 256, no 1‑4, mai 1996, p. 145‑64. DOI.org (Crossref), https://doi.org/10.1016/0040-1951(95)00161-1.
- Livio, Franz, et al. « Growth of Bending-Moment Faults Due to Progressive Folding: Insights from Sandbox Models and Paleoseismological Implications ». Geomorphology, vol. 326, février 2019, p. 152‑66. DOI.org (Crossref), https://doi.org/10.1016/j.geomorph.2018.02.012.
Autres articles intéressants possiblement
- Poulet, M. « Apport des expériences de mécaniques des roches à la géologie structurale des bassins sédimentaires ». Revue de l’Institut Français du Pétrole, vol. 31, no 5, septembre 1976, p. 781‑822. DOI.org (Crossref), https://doi.org/10.2516/ogst:1976026.
31 Janvier 2025
- Nous avons contacté Markus Beckers, un ancien collègue de Janos Urai, pour avoir plus d'informations sur leur modélisation de plis utilisant le silicone et les mousses.
- Nous avons également contacté le responsable de la plateforme Biologie/Chimie du Fablab, Steve Hubert, afin de demander conseil sur les silicones et savoir quand est-ce qu'on peut y avoir accès
(autres : mousse polyéthylène non réticulée)
Objectifs :
- Déterminer la taille de mousses
- Trouver une manière de découper les mousses de façon égales
- Trouver un milieu pour faire couler du silicone entre les 2 mousses
Expérience :
- Mousse utilisée : voir photo suivante
- Taille des mousses : voir schéma suivant - Taille de la couche de silicone : On va choisir 1,5cm d'épaisseur
- Milieu pour faire couler silicone -> carton que l'on va faire à partir des mesures de la taille des mousses.
Figure 1 : mousse utilisée Figure 2 : Schéma des dimensions du "moule" pour les 2 couches de mousses et la couche de silicone
Figure 3 : le carton (1)
Figure 4 : Prototype n°1
- Construction du prototype de montage du "pli" : 2 mousses de même épaisseur avec un espace de 3 cm entre les 2 (emplacement prévu pour le silicone), découpe de la mousse au FabLab prototypage avec une scie.
- Visite du FabLab chimie pour tester la fixation de la mousse avec le silicone.
05 Février 2025
Passage au Fablab Chimie pour observer aller vérifier si le silicone colle / adhère bien à la mousse. Résultat : ça adhère bien.
Test sur plus grande surface et avec un peu plus de silicone, à récupérer le 07/02
07 Février 2025
Passage au Fablab Chimie pour récupérer le test. Résultat : Silicone adhère bien mais il a coulé. Pour régler cela : colle et talc. Si ça ne fonctionne toujours pas, il faudra trouver un autre type de mousse.
Recherche sur des mousses moins poreuses et viscosité de différents silicones :
- Mousse de polyuréthane d'une porosité d'environ 98% dont les pores, d'une taille d'environ trois millimètres, sont fermés par des membranes de 1 à 5 micromètres d'épaisseur.
- Référence : Etude des propriétés rhéologiques et de vulcanisation des élastomères silicones bi-composants - H. OU, M. SAHLI, T. BARRIERE et J.C. GELIN - Institut FEMTO-ST, Département de Mécanique Appliquée, 24 rue de l’Epitaphe, 25000 Besançon, France
- Silicone RTV-A-2186 = grande élasticité (321%) :

- Référence : Polyzois, Gregory L., et al. « An Assessment of the Physical Properties and Biocompatibility of Three Silicone Elastomers ». The Journal of Prosthetic Dentistry, vol. 71, no 5, mai 1994, p. 500‑04. DOI.org (Crossref), https://doi.org/10.1016/0022-3913(94)90190-2.
Hypothèse 2 : Mousse expansive et isolante ?
-> cette hypothèse a été plus ou moins invalidée par le fait que la majorité du temps, les mousses expansives sont très peu souples.
10 Février 2025
Passage au Fablab Chimie pour observer aller vérifier si le silicone de l'expérimentation avec le talc. Résultat : ça fonctionne bien,
le silicone rentre moins dans la mousse et ne va pas totalement au fond.
14 Février 2025
Idées :
0. Envoyer un mail ou aller voir Fablab chimie pour demander si possibilité d'ouverture Fablab chimie jeudi matin + prévoir suffisamment de silicone
- Jeudi matin (entre 08h30 et 10h30) : mettre silicone sur le fond
- Jeudi après-midi (entre 13h45 et 14h45) : mettre mousse sur silicone en train de se durcir progressivement (pour éviter que la mousse s'enfonce trop)
- vendredi : mettre enfin le silicone entre les deux mousses
Faire le format pour le grand prototype n°1. Il faut vérifier qu'avec une grande taille ça fonctionne avec nos mousses.
Volume environnant de silicone utilisé = 1,7*11,5*41,8=817,19cm^3 pour la couche de silicone
Volume environnant de silicone utilisé = 0,5*11,2*41,8=234,08cm^3 pour la base de silicone en dessous pour que ça colle
Volume total de silicone utilisé = 1051,27cm^3, on peut anticiper en considérant qu'il en faut 1070cm^3.
- 1,07L de silicone totalement.
Notre Silicone = RTV 151, de densité d=1,2 - une viscosité de 8000 mPa.s.
20 Février 2025
Passage au Fablab Chimie pour faire la base de silicone de 0,5cm (le matin) puis mise des mousses enduites de talc (pour éviter que le silicone rentre dans la mousse) 1h35 plus tard (avec colle sur les côtés carrés - voir schéma).
On a m=ρ*V donc m=1,25(g/cm^3)*235(cm^3). m=236,25g. On utilise 95% de silicone et 5% de catalyseur.
0,95*236,25=224,44g de silicone et 0,05*236,25=11,81g de catalyseur
21 Février 2025
Passage au Fablab Chimie pour faire la couche de silicone centrale. On anticipe 820cm^3 de silicone.
m=ρ*V donc m=1,25*820=1025g. On va le faire en 4x car on a un petit conteneur. Ainsi, 1025/4=256,25g
Pour 256,25g, on a besoin de 0,95*256,25=243,44g de silicone et 0,05*256,25=12,81g de catalyseur.
Pour les 3 premiers quarts, on a bien fait 243,44g de silicone... mais pour le 4ème, nous n'avions plus assez de silicone donc nous avons utilisé 235,89g de silicone, complétés par 12,42g de catalyseur. Nous n'avons pas réussi à terminer la couche de silicone par manque de silicone. Voici le résultat pour le moment :
Il faut acheter encore du silicone et du catalyseur à silicone.
14 Mars 2025
Aujourd'hui nous sommes allées chercher notre prototype au Fablab chimie. Nous avons découpé 3 faces de carton (le fond et 2 côtés) et le haut de mousse en trop. Nous avons fait des essais de pli en appliquant une force sur le dessus (voir les photos). Ca fonctionne bien. Nous allons refaire un modèle avec une plus grosse épaisseur de mousse (fois 2 ou fois 3) avec peut-être une épaisseur de silicone de 1cm. Les socles en carton se décollent un peu, il faut trouver un moyen de les fixer.
28 Mars 2025
Recherche pour les achats. Pour le silicone : n'importe lequel des 2 silicones suivants : Silicone RTV 120 - Esprit composite ou Silicone RTV 67 - Esprit composite (car dureté plus faible). Pour les mousses, mousse synthétique à cellules ouvertes, diamètre cellulaire ~ 1mm (1000 µ) = mousse isolante + Polyuréthane légère et extra-compressible.
11 Avril 2025
Nous avons construit le "moule" pour notre deuxième prototype et découpé la mousse.
Nos deux plaques de mousses ont des dimensions plus grandes que celles du premier prototype : 64 cm x 4 cm x 22 cm. Nous visons aussi une dimension de silicone différente : le fond fera toujours 0.5 cm de hauteur mais la couche entre les 2 mousses devrait faire : 64 cm x 1.2 cm x 22 cm.
Comme l'espace biologie-chimie était fermé nous en avons profité pour effectuer les calculs préliminaires pour couler le silicone :
Volume environnant de silicone utilisé = 64*1.2*22 = 1690 cm^3 pour la couche centrale de silicone
Volume environnant de silicone utilisé = 0.5*(4+4+1.2)*64 = 295 cm^3 pour la base de silicone en dessous pour que ça colle
Volume total de silicone utilisé = 1690 + 295 = 1985 cm^3, on peut anticiper en considérant qu'il en faut 1991 cm^3
- 1.991 L de silicone totalement.
Notre Silicone = R15, de densité d=1,051 - une viscosité de 1.39 mPa.s
"socle" : On a m=ρ*V donc m=1.051*301 <=> m=317g
On utilise 95% de silicone et 5% de catalyseur.
m=0.95*317 <=> m=301g de silicone et m=0.05*317 <=> m=16g de catalyseur
couche centrale : m=ρ*V donc m=1.051*1690 <=> m=1777g
On utilise 95% de silicone et 5% de catalyseur.
m=0.95*1777 <=> m=1689g de silicone et m=0.05*1777 <=> m=82g de catalyseur
On va le faire en 3x car on a un petit conteneur. Ainsi, on a, pour chaque fois qu'on le fait : m=563g de silicone et m=28g de catalyseur.
02 Mai 2025
Nous avons coulé le silicone entre nos 2 couches de mousse. Malheureusement nous n'avons pas eu assez de silicone pour remplir en entier, nous découperons donc la mousse en trop. La question, c'est pourquoi n'avons-nous pas assez de silicone ?
09 Mai 2025
Nous avons constaté que le silicone n'était pas aussi peu dense que nous le voulions et il a crée un gradient dans la mousse. Le gradient explique aussi peut-être pourquoi nous n'avions pas assez de silicone (hypothèse). De plus la couche de silicone de fond était trop solidement accroché donc nous avons dû scié le fond et le surplus de mousse ce qui donne un résultat moins propre. Le talk semble ne pas avoir fait autant effet qu'avec le silicone de la première expérience.
Nous avons tracé des repères pour constaté les extensions, etc.
Premier modèle :
Avec échelle :
Deuxième modèle :
Avec échelle :
Remerciements
A toute l'équipe de l'UE Fablab de Géosciences ainsi qu'aux responsables du Fablab Chimie/Biologie pour leurs conseils et leur temps.
































No Comments